Determining Whether A Function Is One
Some functions have a given output value that corresponds to two or more input values. For example, in the stock chart shown in the figure at the beginning of this chapter, the stock price was $1000 on five different dates, meaning that there were five different input values that all resulted in the same output value of $1000.
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in Table 12.
| Letter grade |
|---|
| 1.0 |
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
To visualize this concept, letâs look again at the two simple functions sketched in Figure 1 and Figure 1. The function in part shows a relationship that is not a one-to-one function because inputs q n . The function in part shows a relationship that is a one-to-one function because each input is associated with a single output.
Using The Horizontal Line Test
Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test. Draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.
Functions And Function Notation
In this section, you will:
- Determine whether a relation represents a function.
- Find the value of a function.
- Determine whether a function is one-to-one.
- Use the vertical line test to identify functions.
- Graph the functions listed in the library of functions.
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Don’t Miss: Unit 1 Test Study Guide Geometry Basics Answer Key
The Domain And Range Of A Function Fluency Common Core Algebra Ii Homework 1
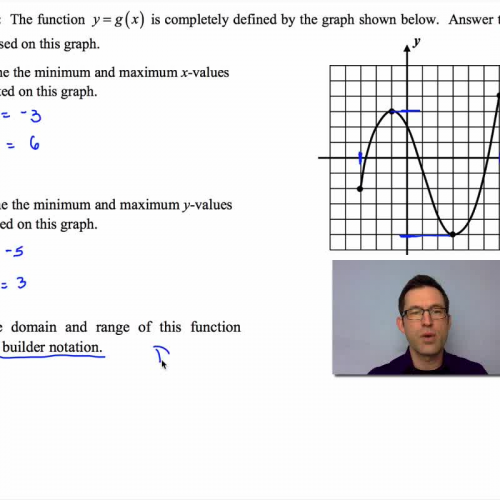
The domain and range of a function common core algebra 1 homework answers. Posted on october 27 2014 september 18 2018 by kirk weiler 1 comment unit 3 lesson 7 the domain and range of a function this final lesson in unit 3 introduces students to the two fundamental sets involved in the function process the domain and range. The function y g x is completely defined by the graph shown below. The graph of f is the graph of the equation y f x.
Y gx is completely defined by the graph shown below. Domain and range of functions. Determine the domain and range of exponential functions.
8 1 functions domain and range. A function is given by the set of ordered. Algebra 1 unit 2 linear equations.
Domain and range homework name hour domain range function. Show the domain and range in the mapping diagram below. Answer the following questions based on this graph.
Show the domain and range in the mapping diagram below. College algebra questions on finding the domain and range of functions with answers are presented. Fn n 2 1 if its domain is the set 1 3 5.
College algebra questions with answers sample 5. If f is a function and x is an element of its domain then f x denotes the output of f corresponding to the input x. F if a 1 understand that a function from one set called the domain to another set called the range assigns to each element of the domain exactly one element of the range.
Pin On Tpt Math Lessons
Finding Input And Output Values Of A Function
When we know an input value and want to determine the corresponding output value for a function, we evaluate the function. Evaluating will always produce one result because each input value of a function corresponds to exactly one output value.
When we know an output value and want to determine the input values that would produce that output value, we set the output equal to the functionâs formula and solve for the input. Solving can produce more than one solution because different input values can produce the same output value.
Evaluation of Functions in Algebraic Forms
When we have a function in formula form, it is usually a simple matter to evaluate the function. For example, the function f x 2 can be evaluated by squaring the input value, multiplying by 3, and then subtracting the product from 5.
Also Check: Who Are Paris Jackson’s Biological Parents
Determining Whether A Relation Represents A Function
A relation is a set of ordered pairs. The set consisting of the first components of each ordered pair is called the domain and the set consisting of the second components of each ordered pair is called the range. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.
The domain is The range is
Note that each value in the domain is also known as an input value, or independent variable, and is often labeled with the lowercase letterEach value in the range is also known as an output value, or dependent variable, and is often labeled lowercase letter
A functionis a relation that assigns a single element in the range to each element in the domain. In other words, no x-values are repeated. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, is paired with exactly one element in the range,
Now lets consider the set of ordered pairs that relates the terms even and odd to the first five natural numbers. It would appear as
Notice that each element in the domain, is not paired with exactly one element in the range, For example, the term odd corresponds to three values from the domain, and the term even corresponds to two values from the range, This violates the definition of a function, so this relation is not a function.
Figure 1.
Using The Vertical Line Test
As we have seen in some examples above, we can represent a function using a graph. Graphs display a great many input-output pairs in a small space. The visual information they provide often makes relationships easier to understand. By convention, graphs are typically constructed with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value x when the function is named f The graph of the function is the set of all points . If the function is defined for only a few input values, then the graph of the function is only a few points, where the x-coordinate of each point is an input value and the y-coordinate of each point is the corresponding output value. For example, the black dots on the graph in Figure 7 tell us that f However, the set of all points ( is a curve. The curve shown includes ( because the curve passes through those points.
The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value. See Figure 8.
Recommended Reading: What Is Ap Biology In High School
Common Core Algebra 1
Entire contents Copyright © – All rights reserved. Reproduction of this publication in any form without prior written permission is forbidden. is the manager of this website.
Frederick County Public Schools is not responsible for the content of externally authored links included on FCPS webpages.
Premium Drupal Theme by Adaptivethemes.com
Identifying Basic Toolkit Functions
In this text, we will be exploring functionsâthe shapes of their graphs, their unique characteristics, their algebraic formulas, and how to solve problems with them. When learning to read, we start with the alphabet. When learning to do arithmetic, we start with numbers. When working with functions, it is similarly helpful to have a base set of building-block elements. We call these our âtoolkit functions,â which form a set of basic named functions for which we know the graph, formula, and special properties. Some of these functions are programmed to individual buttons on many calculators. For these definitions we will use x as the input variable and y
Read Also: Exponent Rules Worksheet Answer Key
How To
Given a relationship between two quantities, determine whether the relationship is a function.