What Does Parentheses Mean In Math

Using A Number Line To Add Integers

Use a number line to solve + 7.

Start at -5 and jump 7 places in the positive direction . You’ll land on the answer, +2.

Look Out: sometimes you may see parentheses around negative numbers. These do not mean that we need to multiply they’re just used so that we don’t confuse negatives with subtraction.

Lie Bracket And Commutator

In group theory and ring theory, square brackets are used to denote the commutator. In group theory, the commutator is commonly defined as g1h1gh. In ring theory, the commutator is defined as abba. Furthermore, braces may be used to denote the anticommutator: is defined as ab + ba.

The Lie bracket of a Lie algebra is a binary operation denoted by :}\times }\to }} . By using the commutator as a Lie bracket, every associative algebra can be turned into a Lie algebra. There are many different forms of Lie bracket, in particular the Lie derivative and the JacobiLie bracket.

Common Mistakes While Using Pemdas Rule In Math

The presence of multiple brackets usually causes confusion. If we don’t know which bracket to solve first, it could lead to an incorrect answer. We will now learn how to solve this expression with multiple brackets.

4+3÷2

We will begin with working from the inside of the brackets. We will solve the inner-most bracket first and then move outside.

• Starting with 6 3 = 3, we get: 4 + 3 ÷ 2
• Next, multiplying 2=6 or 2×3=6, we get: 4 + 3 ÷ 2
• There is one bracket left, = 2, we get: 4 + 3 ÷ 2
• Solving 3 or 3 × 2 = 6, we have: 4 + 6 ÷ 2

We can observe that all the expressions in the brackets are solved. Based on PEMDAS, we know that division comes next, hence, 6 ÷ 2 = 3, that is, 4 + 3. And lastly, addition 4 + 3 = 7.

Related Articles

Check out the few more interesting articles related to PEDAS and rules. Learn the difference between BODMAS and PEMDAS with the help of the following articles.

You May Like: How To Analyze People With Psychology

Finding The Domain Of A Function With An Even Root

Find the domain of the function\,f\left=\sqrt.

When there is an even root in the formula, we exclude any real numbers that result in a negative number in the radicand.

Set the radicand greater than or equal to zero and solve for\,x.

Now, we will exclude any number greater than 7 from the domain. The answers are all real numbers less than or equal to\,7,\,or\,\left(-\infty ,7\right].

What Is It Called When You Multiply Numbers In Parentheses

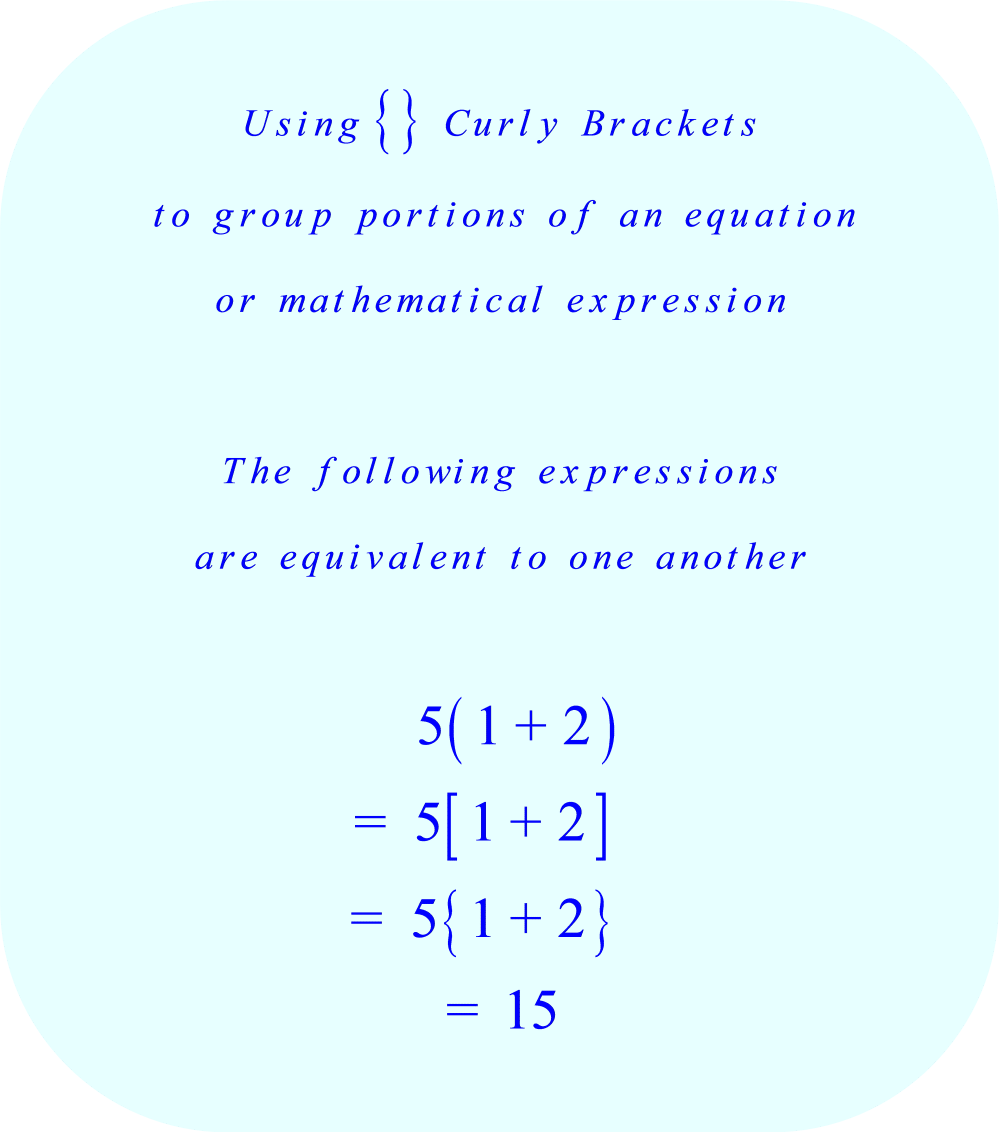
When an expression has two sets of parentheses next to each other, you need to multiply every term inside the first set of parentheses by every term in the second set. This process is called FOILing.

What do you call the number outside the parentheses?

Algebraic distribution means to multiply each of the terms within the parentheses by another term that is outside the parentheses. Multiply each term by the number and/or variable outside of the parentheses. 2 + 2 2 Perform the multiplication operation in each term.

What are the parts of a math problem called?

There are three main parts to a division problem: the dividend, the divisor, and the quotient. The dividend is the number that will be divided.

You May Like: Why Is Geography Important To History

Using Notations To Specify Domain And Range

In the previous examples, we used inequalities and lists to describe the domain of functions. We can also use inequalities, or other statements that might define sets of values or data, to describe the behavior of the variable in set-builder notation. For example,\,\left\\,describes the behavior of\,x\,in set-builder notation. The braces\,\left\\,are read as the set of, and the vertical bar | is read as such that, so we would read\,\left\\,as the set of x-values such that 10 is less than or equal to\,x,\,and\,x\,is less than 30.

compares inequality notation, set-builder notation, and interval notation.

Figure 5.

To combine two intervals using inequality notation or set-builder notation, we use the word or. As we saw in earlier examples, we use the union symbol,\,\cup ,to combine two unconnected intervals. For example, the union of the sets\left\\,and\,\left\\,is the set\,\left\.\,It is the set of all elements that belong to one or the other of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is

Working With A Piecewise Function

A cell phone company uses the function below to determine the cost,\,C,\,in dollars for\,g\,gigabytes of data transfer.

Find the cost of using 1.5 gigabytes of data and the cost of using 4 gigabytes of data.

To find the cost of using 1.5 gigabytes of data,\,C\left,\,we first look to see which part of the domain our input falls in. Because 1.5 is less than 2, we use the first formula.

To find the cost of using 4 gigabytes of data,\,C\left,\,we see that our input of 4 is greater than 2, so we use the second formula.

Analysis

The function is represented in . We can see where the function changes from a constant to a shifted and stretched identity at\,g=2.\,We plot the graphs for the different formulas on a common set of axes, making sure each formula is applied on its proper domain.

Figure 24.

Don’t Miss: What Is Ucr In Psychology

What Are The Basics Of Positive And Negative Numbers

Basics of Positive and Negative Numbers. Zero separates the positive numbers from the negative ones. In a line with zero in the middle, negative numbers line up on the left, and positive numbers line up on the right: 4, 3, 2, 1, 0 1, 2, 3, 4. When you visualize negative and positive numbers in a line like this,

What are the rules for subtracting negative numbers?

Here are some simple rules to follow when subtracting negative numbers. Rule 1: Subtracting a positive number from a positive number its just normal subtraction. For example: this is what you have learned before. 6 3 are two positive numbers.

Parentheses Definition In Math

Parenthesis, also known as round brackets, are defined as the symbols in Math. Parenthesis are primarily used in Mathematics/Algebraic equations to modify the normal order of operation. Hence, in Mathematic expressions involving Parentheses, the terms inside the bracket or parenthesis are calculated first.

For example, In an expression like 6, the part of Mathematical expression within the parenthesis is calculated first = 7, then this result is used to calculate the rest of the expression 7 6 = 42. Therefore, 6 = 42.

Read Also: How Many Biological Children Does Angelina Jolie Have

Interval Notation How And Where To Use It

In mathematics, we want to be as efficient and accurate as possible when explaining certain principles. One such example is the interval notation. An interval is a range of real numbers between a and b in a < b that contains all real numbers from the specified start point a to the specified endpoint b. This notation frequently shows up in Algebra and other advanced math when displaying an interval.

Interval notation describes the set containing all real numbers between the lower and upper bounds, which might not be included. Endpoint values are listed in parentheses/brackets. Square brackets indicate they lie within the set, and parentheses indicate they dont lie within the set. For example given (3,15], 3 is not included while 15 is.

Floor/ceiling Functions And Fractional Part

Square brackets, as in = 3, are sometimes used to denote the floor function, which rounds a real number down to the next integer. Respectively, some authors use outwards pointing square brackets to denote the ceiling function, as in ][ = 4. However, the floor and ceiling functions are usually typeset with left and right square brackets where only the lower or upper horizontal bars are displayed, as in = 3 or = 4.

Braces, as in < 1/7, may denote the fractional part of a real number.

Recommended Reading: How Did Northern European Geography And Technology Affect Each Other

What Does A Bracket Mean In Domain

Braces or curly brackets are used when the domain or range consists of discrete numbers and not an interval of values. If the domain or range of a function is all numbers, the notation includes negative and positive infinity . If the domain is all positive numbers plus 0, the domain would be written as [0,).

Finding The Domain Of A Function Defined By An Equation

In Functions and Function Notation, we were introduced to the concepts of domain and range. In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0.

We can visualize the domain as a holding area that contains raw materials for a function machine and the range as another holding area for the machines products. See .

Figure 2.

We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket \,\left(0,\text100\right].\,We will discuss interval notation in greater detail later.

Before we begin, let us review the conventions of interval notation:

See for a summary of interval notation.

Figure 3.

Also Check: What Does Symbiosis Mean In Biology

What Does Parentheses Mean On A Negative Number

Definition of Amounts in Parentheses For example, parentheses could indicate any of the following: A negative amount, such as a negative balance in your check register. The meaning of a negative amount in a series of amounts, such as the bottom line of a comparative income statement that states Net income

What do you do with a negative number in parentheses?

Math books often put parentheses around the negative number youre subtracting so the signs dont run together, so 3 5 is the same as 3 .

What Does A Number Over A Number In Parentheses Mean

Parentheses are used to enclose the variables of a function in the form , which means that values of the function are dependent upon the values of . 4. Large parentheses around two numbers, one above the other, denotes a binomial coefficient .

What do parentheses mean in a problem?

Parentheses are used to group numbers or variables, or both. When you see a math problem containing parentheses, you need to use the order of operations to solve it. For example, take the problem: 9 5 ÷ x 2 + 6.

What does parentheses mean in calculus?

A notation for representing an interval as a pair of numbers. The numbers are the endpoints of the interval. Parentheses and/or brackets are used to show whether the endpoints are excluded or included. For example, [3, 8) is the interval of real numbers between 3 and 8, including 3 and excluding 8.

Don’t Miss: What Is Time In Physics

What Do Numbers Inside Parentheses Mean

Numbers in Parentheses A number listed on the financial statements that in contained within parentheses is a negative number. If there are no parentheses the number is positive. The final row of the Statement of Revenue & Expenses report shows the Revenue in Excess of Expenses also known as Net Income.

What Does 2 Parentheses Mean

The first way tells us to multiply. When we see two or more numbers together that are separated by parentheses, then the parentheses are telling us to multiply. For example, when we see 5, the parentheses are telling us to multiply the 5 and the 2 together.

Do parentheses mean negative?

Numbers in Parentheses A number listed on the financial statements that in contained within parentheses is a negative number. If there are no parentheses the number is positive. Statement of Revenue & Expenses This report shows the monthly billed income and incurred expenses.

What do brackets parentheses mean?

Key Difference: Brackets and parentheses are symbols used for enclosing words or numbers. Parenthesis is used if the point is not being included in the interval, whereas a bracket is used when the point is included. For example (5, 6] This means that 5 is excluded and 6 is included in this interval.

What does it mean when there are parentheses around a negative number in math?

Math books often put parentheses around the negative number youre subtracting so the signs dont run together, so 3 5 is the same as 3 . When taking a negative number minus a positive number, drop both minus signs and add the two numbers as if they were both positive then attach a minus sign to the result.

Which is an example of the factorial function?

Example: 4! is shorthand for 4 x 3 x 2 x 1. The factorial function says to multiply all whole numbers from our chosen number down to 1.

Read Also: What Is The Unit For Distance In Physics

Do You Multiply Or Add First Without Brackets

The order of operations can be remembered by the acronym PEMDAS, which stands for: parentheses, exponents, multiplication and division from left to right, and addition and subtraction from left to right. There are no parentheses or exponents, so start with multiplication and division from left to right.

Finding Domain And Range From A Graph Of Oil Production

Find the domain and range of the function\,f\,whose graph is shown in .

Figure 11.

The input quantity along the horizontal axis is years, which we represent with the variable\,t\,for time. The output quantity is thousands of barrels of oil per day, which we represent with the variable\,b\,for barrels. The graph may continue to the left and right beyond what is viewed, but based on the portion of the graph that is visible, we can determine the domain as\,1973\le t\le 2008\,and the range as approximately\,180\le b\le 2010.

In interval notation, the domain is , and the range is about . For the domain and the range, we approximate the smallest and largest values since they do not fall exactly on the grid lines.

Also Check: Geometry Segments And Angles Worksheets

Order Of Arithmetic Operations In Particularthe 48/2 Question

A problem that hit the Internet in early 2011 is, “Whatis the value of 48/2 ?”

Depending on whether one interprets the expressionas or as 48/) one gets 288 or 2. There is no standard convention as to which of these two waysthe expression should be interpreted, so, in fact, 48/2 is ambiguous. To render it unambiguous, one should writeit either as or 48/). This applies, in general, to any expression of theform a/bc : one needs to insertparentheses to show whether one means c or a/.

In contrast, under a standard convention,expressions such as ab+c areunambiguous: that expression means only +c andsimilarly, a+bc means only a+. The convention is that when parentheses are not used toshow the contrary, multiplication precedes addition i.e., in ab+c, one first multipliesout ab, then adds c to the result, whilein a+bc, one first multipliesout bc, then adds the result to a. For expressions such as ab+c, or a+bc, or abc, there is also afixed convention, but rather than saying that one of additionand subtraction is always done before the other, it says that when onehas a sequence of these two operations, one works from left toright: One starts with a, then adds orsubtracts b, and finally adds or subtracts c.

Lets Look At The Difference Between And

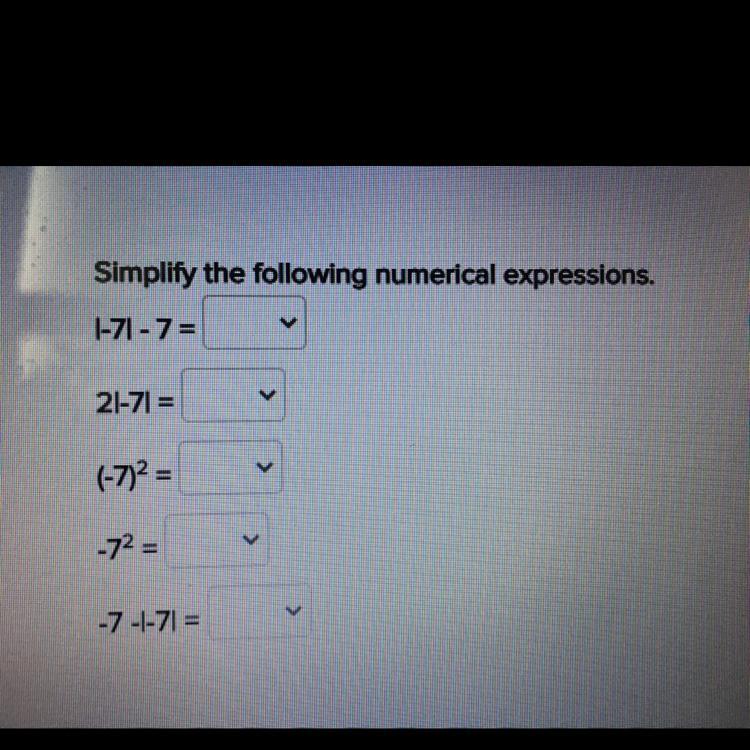
If the base is in parentheses, as in our first case, the exponent affects everything that is inside the parenthesis, that is, the sign and the number.

However, if the base is not in parentheses, as in the second case, the exponent affects only the immediate value to the left, that is, only the number, without the sign.

As you can see, a pair of parentheses can totally change the result.

Lets see some more examples of handling parentheses in the powers.

You May Like: What Is Sn In Chemistry

What Is 2 + 4 7

Solution:

Following the precise order of operation, we get the following:

2 + 4 ) 7 Adding terms inside the small parentheses gives

= 2 + 4 ) 7 Calculating the exponents inside the small parentheses gives

= 7 Adding the terms inside the parentheses.

= 7 Multiplying the terms gives

= 203 Result

The four important parentheses rules are discussed below:

Example: 5 + = 5 – 3 = 2

Example: 5 – = 5 + 3 = 8

Example: = 5 3 = 15

Finding The Domain And Range

Find the domain and range of\,f\left=2\sqrt.

We cannot take the square root of a negative number, so the value inside the radical must be nonnegative.

The domain of\,f\left\,is\,\left

We then find the range. We know that\,f\left=0,\,and the function value increases as\,x\,increases without any upper limit. We conclude that the range of\,f\,is\,\left

Analysis

represents the function\,f.

Figure 22.

Find the domain and range of\,f\left=-\sqrt.

domain:\,\left(-\infty ,2\right] \,range:\,\left(-\infty ,0\right]

Don’t Miss: What Makes Something Living Biology