What Is Time In Physics

Electromagnetism And The Speed Of Light

In 1864, James Clerk Maxwell presented a combined theory of electricity and magnetism. He combined all the laws then known relating to those two phenomenon into four equations. These vector calculus equations which use the del operator are known as Maxwell’s equations for electromagnetism.

In free space , the equations take the form :

is the speed of light in free space, 299 792 458 m/s;

E is the electric field;

B is the magnetic field.

These equations allow for solutions in the form of electromagnetic waves. The wave is formed by an electric field and a magnetic field oscillating together, perpendicular to each other and to the direction of propagation. These waves always propagate at the speed of light c, regardless of the velocity of the electric charge that generated them.

The fact that light is predicted to always travel at speed c would be incompatible with Galilean relativity if Maxwell’s equations were assumed to hold in any inertial frame , because the Galilean transformations predict the speed to decrease in the reference frame of an observer traveling parallel to the light.

It was expected that there was one absolute reference frame, that of the luminiferous aether, in which Maxwell’s equations held unmodified in the known form.

Galileo: The Flow Of Time

In 1583, Galileo Galilei discovered that a pendulum’s harmonic motion has a constant period, which he learned by timing the motion of a swaying lamp in harmonic motion at mass at the cathedral of Pisa, with his pulse.

In his Two New Sciences , Galileo used a water clock to measure the time taken for a bronze ball to roll a known distance down an inclined plane; this clock was

“a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water, which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for a part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results.”

Galileo’s experimental setup to measure the literal flow of time, in order to describe the motion of a ball, preceded Isaac Newton‘s statement in his Principia:

I do not define time, space, place and motion, as being well known to all.

The Galilean transformations assume that time is the same for all reference frames.

What Scientists Still Don’t Know

Despite its intricacy, relativity remains the best way to account for the physical phenomena we know about. Yet scientists know that their models are incomplete because relativity is still not fully reconciled with quantum mechanics, which explains the properties of subatomic particles with extreme precision but does not incorporate the force of gravity.;

Quantum mechanics rests on the fact that the tiny bits making up the universe are discrete, or quantized. So photons, the particles that make up light, are like little chunks of light that come in distinct packets.

Some theorists have speculated that perhaps space-time itself also comes in these quantized chunks, helping to bridge relativity and quantum mechanics. Researchers at the European Space Agency have proposed the Gamma-ray Astronomy International Laboratory for Quantum Exploration of Space-Time mission, which would fly around our planet and make ultra-accurate measurements of distant, powerful explosions called gamma-ray bursts that could reveal the up-close nature of space-time.;

Such a mission wouldn’t launch for at least a decade and a half but, if it did, it would perhaps help solve some of the biggest mysteries remaining in physics.;

Recommended Reading: Geometry Segment Addition Postulate Worksheet

Everything Does Not Happen Simultaneously

This does not mean that everything is happening simultaneously, however. In fact, Einstein firmly believedbased on the evidence of his equations that no information can travel faster than the speed of light. Every point in space-time is limited in the way it can communicate with other regions of space-time. The idea that everything happens simultaneously is exactly counter to the results that Einstein developed.

This and other physics errors in The Secret are perfectly understandable because the fact is these are very complex topics, and they are not necessarily completely understood by physicists. However, just because physicists don’t necessarily have a complete understanding of a concept such as time does not mean that it’s valid to say they have no understanding of time, or that they’ve written off the whole concept as unreal. They most assuredly have not.

Remarks And Limitations On The Toy Models

The two toys models presented above have the virtue of beingmathematically tractable, but they involve certain simplifications andpotential problems that lead to trouble if one tries to make them morecomplicated. Working through these difficulties will help highlight theconditions we have made use of.

Consider a slight modification of the first simple model proposed tous by Adam Elga. Let the particles have an electric charge,which produces forces according to Coulombs law. Then set up asituation like that depicted in figure 9:

Figure 9: Set-up for Elga’s Paradox

The dotted line indicates the path the particle will follow if noforces act upon it. The point labeled P is the left edge ofthe time-travel region; the two labels are a reminder that the point atthe bottom and the point at the top are one and the same.

Elga’s paradox is as follows: if no force acts on the particle, thenit will enter the time-travel region. But if it enters the time travelregion, and hence reappears along the bottom edge, then its later selfwill interact electrically with its earlier self, and the earlier selfwill be deflected away from the time-travel region. It is easy to setup the case so that the deflection will be enough to keep the particlefrom ever entering the time-travel region in the first place. But, of course, if the particle never entersthe region at all, then it will not be there to deflectitself.

Figure 10: Elga’s Paradox with a Charged Bar

Figure 12

Recommended Reading: Write The Segment Addition Postulate For The Points Described

What Does The Future Hold

Mlodinow and Brun, the researchers, point out in their paper that their work focuses on a classical view with memory subsystems that have well-defined states at any time.1 Their arguments cannot be directly applied to quantum systems that involve entangled states, which are not definite states at a given time. The researchers are working on an argument for quantum systems. For work on quantum systems that has been done so far, see references 5 and 6.

For more on the direction of time and relativity see the appendix below.

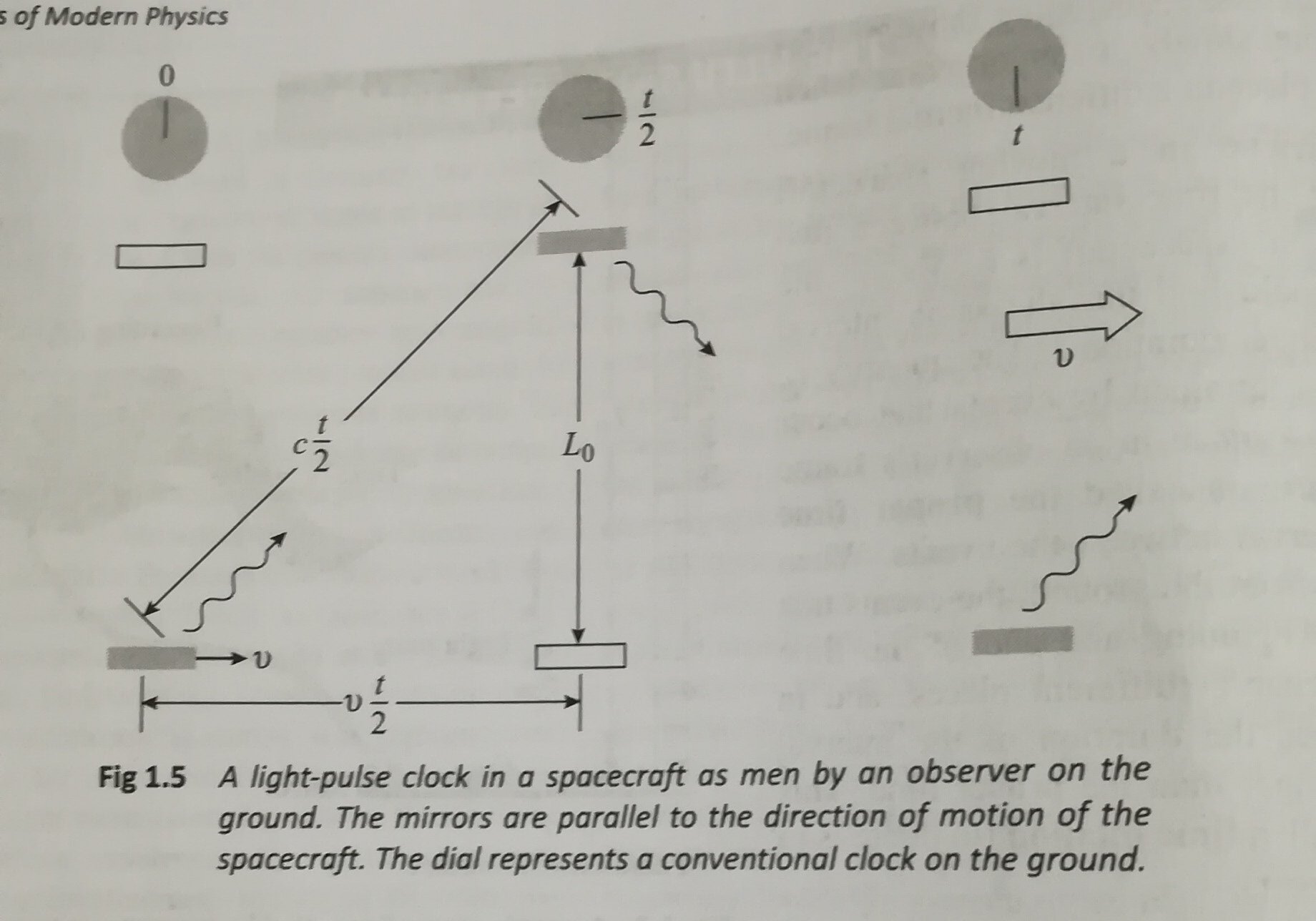
The Clock: A Predictably Regular Motion

In physics,;any predictable, regular motion can be used as a clock.;;A great many clocks have been developed, from the common wrist watch that marks the passage of each day, to isotopic decay, which is used to measure;time on a geological and archeological scale.;;First, lets look at your wristwatch.;;It most likely operates using a;quartz crystal resonator,;;which amplifies a particular frequency of input power.;;The crystals vibrational frequency is determined by its shape and cut, and each watch contains a piece of quartz that is;tuned;to vibrate at a standardized rate of 32,768 times per second. This standard rate is mechanically translated to the consistent movement of the hands across the watch face, which results in a consistent response to do you have the time?

Quartz vibrates regularly with electric stimulation, making it a great clock. Image: Thad Zajdowicz

Quartz is not the only possible clock oscillator. To tell time using caesium-133, physicists use its predictable transitions between quantum energy levels. Caesium crystals breathe through this transition some 9,192,631,770 times a second – 280,000 times faster than quartz – and can be used for highly precise atomic clocks. They;have become the gold standard for quantifying Earth time, but there is a tiny catch. Do they always tell the same time?

The first atomic clock was produced at Columbia University and later adapted for Cesium, pictured above at the UK National Laboratory. Image: Wikimedia.

Read Also: What Is The Molecular Geometry Of Ccl4

Velocity Boosts In Str And Classical Mechanics

STR and classical mechanics have exactly the same symmetries under translations of time and space, and rotations of space. They also both have symmetries under velocity boosts: both theories hold that, if we take a valid physical process, and give it a uniform additional velocity in some direction, we end with another valid physical process. But the transformation of space and time coordinates, and of proper time, are different for the two theories under a velocity boost. In classical physics, it is called a Galilean transformation, while for STR it is called a Lorentz transformation.

To see how the difference appears, we can take a stationary trajectory, and consider what happens when we apply a velocity boost in either theory.

Figure 4. Classical and STR Velocity Boosts give different results.

In both diagrams, the green line is the original trajectory of a stationary particle, and it looks exactly the same in STR and classical mechanics. Proper time events are equally spaced with the coordinate time intervals in both cases.

If we transform the classical trajectory by giving the particle a velocity towards the right, the result is very simple: the proper time events remain equally spaced with coordinate time intervals. The same sequence of proper time events takes the same amount of coordinate time to complete. The classical particle moves a distance: Dx = v.Dt to the right, where Dt is the coordinate time duration of the original process.

Dt = Dt, and: Dx = vDt

and:

Choice Of Inertial Reference Frame

A second crucial concept is the idea of a reference frame. A reference frame specifies all the trajectories that are regarded as stationary, or at rest in space. This defines the property of remaining at the same place through time. But the key feature of both classical mechanics and STR is that no unique reference frame is determined. Any object that is not accelerating can be regarded as stationary in its own inertial frame. It defines a valid reference frame for the whole universe. This is the natural reference frame from the point of view of the object, or relative to the object. But there are many possible choices because given any particular reference frame, any other frame, defined to give everything a constant velocity relative to the first frame is also a valid choice.

The idea of the conventionality of the reference frame is partly evident already in the choice of a Cartesian coordinate system: for it is an arbitrary matter where we choose the origin, or point: 0 = , for such a system. It is also arbitrary which directions we choose for the x, y, and z axes as long as we make them mutually perpendicular. We are free to rotate a given set of axes, x, y, z, to produce a new set, x, y, and z, and this gives another Cartesian coordinate system. Thus, translations and rotations of Cartesian coordinate systems for space still leave us with Cartesian systems.

Read Also: Eoc Fsa Warm Ups Algebra 1 Answers

Time And Space Dilation

Figure 7 shows how both time and space dilation effects work. To see this clearly, we need to consider the volumes of space-time that an object like a rod traces out.

• The rectangle PQRS represents a space-time volume, for a stationary rod or ruler in the original frame. It is 1-meter long in original coordinates , and is shown over 1 unit of proper time, which corresponds to one unit of coordinate time .
• The rectangle PQRS represents a second space-time volume, for a rod which appears to be moving in the original frame. This is how the space-time volume of the first rod transforms under a Lorentz transformation.
• We may interpret the transformation as either: a Lorentz velocity boost of the rod by velocity +V , or equally: a Lorentz transformation to a new coordinate system, , moving at V with regard to . Note that:
• The length of the moving rod measured in x is now shorter than the stationary rod: Dx = 1/. This is space dilation.
• The coordinate time between proper time events on the moving rod measured in t is now longer than for the stationary rod . This is time dilation.

The need to fix the new coordinate system in this way can be worked out by considering the moving rod from the point of view of its own inertial system.

The Thermodynamic Arrow Of Time

Scientists have accumulated strong evidence for the second law of thermodynamics, which states that natural processes tend to move toward increased entropy. Entropy measures the level of disorder or randomness of a system, and natural processes tend to cause more disorder.

You may not believe that disorder tends to increase when you consider the amazing order that occurs when you clean your room, but you also have to consider the amount of disorder that occurs due to your body working to clean up your room. While you are making your room look more ordered macroscopically, your body and the environment are heating up, causing more disorder on the microscopic level.

Even a highly organized organism results in more entropy overall in its environment during its creation and existence. Humans are clearly highly evolved and organized entities, but we create a lot of waste and disorder to our environment in the physical sense .

You could think of an idealized situation where you isolate a system and make it undergo a special, reversible process that does not heat up the environment, and in this case, it is possible that the entropy could remain the same. And although it is extremely unlikely for the entropy to decrease during a natural process, it is not fundamentally disallowed.

The expansion of the universe.Image Credit: NASA

Recommended Reading: Geometry Segment Addition Postulate Worksheet

Appendix: The Direction Of Time And Relativity

It turns out time is relative. First, letâs examine a classic, and classical, example of relativity. Imagine you are sitting in a train that moves at 100 miles per hour northward. As the train passes a train station, an observer at the train station measures your speed to be 100 miles per hour to the north.

A person on the train measures your speed as zero. If you got up and started walking with constant velocity of 2 miles per hour southward, then the observer at the train station would measure your velocity at 98 miles per hour to the north. A person on the train would measure your velocity as 2 miles per hour to the south. Your speed is relative.

This is classical relatively. The speeds involved are much smaller than the speed of light in vacuum, there is no acceleration, and we consider time and space to be the same for all observers.

There are problems with classical relativity. It does not describe well the measured results of certain observations and Maxwellâs equations, which describe electromagnetic phenomena, do not follow it this classical relativity.

Now we have two sides to this picture. Light can follow curved paths due to nearby massive objects, and light travels along a trajectory in space-time, which can be curved due to massive objects. What if these formed a closed curve, or a loop? Is it possible? For more on this see reference 2.

The Str Relationship Between Space Time And Proper Time

STR predicts that motion of a system through space is directly compensated by a decrease in real internal processes, or proper time rates. Thus, a clock will run fastest when it is stationary. If we move it about in space, its rate of internal processes will decrease, and it will run slower than an identical type of stationary clock. The relationship is precisely specified by the most profound equation of STR, usually called the metric equation . The metric equation is:

This applies to the trajectory of any physical system. The quantities involved are:

D is the difference operator.

Dt is the amount of proper time elapsed between two points on the trajectory.

Dt is the amount of real time elapsed between two points on the trajectory.

Dr is the amount of motion through space between two points on the trajectory.

c is the speed of light, and depends on the units we choose for space and time.

The meaning of this equation is illustrated by considering simple trajectories depicted in a space-time diagram.

Figure 1. Two simple space-time trajectories.

Trajectories in Figure 1

We can compare this situation with classical physics, where we have two independent equations:

Dt = Dt

Dr = vDt for some

• Equation just means that the rate of proper time in a system is invariant and we measure it in the same units as coordinate time, t.
• Equation just means that every particle or system has some finite velocity or speed, v, through space, with v defined by: v = Dr/Dt.

Read Also: Ccl4 Bond Angle

B Causality And The Arrow Of Time In Special Relativity

Within the CA interpretation of quantum mechanics, special relativity is difficult to handle in this procedure, since the Lorentz group, or the Poincaré group, are notoriously difficult to implement, as these groups are not compact. It is quite conceivable that Poincaré transformations link ontological states not to other ontological states, but to superpositions of ontological states. Yet the presence or absence of symmetries should not be our immediate concern. We may for instance assume that only the homogeneous part of the Lorentz group is a genuine symmetry at the ontological level, or possibly an approximate symmetry.

The more important feature of special relativity is the fact that it gives a limit to the propagation speed of signals. Now this is quite easy to impose on CA models or theories. We just assume that, at the beat of our clock, the contents of a given cell of our automaton can only be passed on to a neighboring cell. Signals then can never propagate faster than the speed of this process. Outside the associated light cone, the validity of No Bell Telephone, Equation , is then guaranteed.

The difficulty of imposing Lorentz- and Poincaré symmetry for CA models continues when time reversibility is broken at the ontological level, but models where the propagation speed of information is limited can easily be extended to being non-reversible in time as well. This happens almost automatically.