What Does The Discriminant Tell You
The discriminant is important in algebra because it tells us the nature of the solutions to a quadratic equation. This distinction is made by the sign of the discriminant:
- D < 0: in this case, the discriminant is negative, which happens when b2< 4ac. This means that there are two complex conjugate solutions to the quadratic equation.
Remember that for each quadratic equation, we can draw the graph of a corresponding parabola .
The discriminant gives us some information about the parabola and what it looks like. Specifically, the discriminant tells us whether the parabola intersects the x-axis, and how many times it does so.
Keep in mind that the points where the parabola intersects the x-axis are the values of x that satisfy the quadratic equation when it is set equal to zero. These values are called solutions or roots of the equation.
Question: What Is Discriminant In Math Example
Discriminant, in mathematics, a parameter of an object or system calculated as an aid to its classification or solution. In the case of a quadratic equation ax2 + bx + c = 0, the discriminant is b2 4ac for a cubic equation x3 + ax2 + bx + c = 0, the discriminant is a2b2 + 18abc 4b3 4a3c 27c2.
How Do You Know If The Discriminant Is Negative
Here are some ways to know that the discriminant is negative, based on the signs of a, b, and c:
- If a and c have the same sign, then ac is positive, which means 4ac is positive, and -4ac is negative. If b is zero, then b2 is zero, and in that case, the discriminant b2 4ac will be negative.
- If a and c have the same sign, but b is not zero, then we must have b2< 4ac in order to have a negative discriminant.
| Scenario |
|---|
If c is zero, then the discriminant cannot be negative, since b2 4ac reduces to b2, which is always positive or zero .
This makes sense, since a value of c = 0 would give us:
- ax2 + bx + c = 0
- ax2 + bx + 0 = 0
- x = 0
This implies x = 0 or ax + b = 0 as solutions, which leaves us with two real solutions: x = 0 and x = -b/a.
Example 1: Negative Discriminant
Consider the quadratic equation 3×2 + 7 = 0.
Since it has the form ax2 + bx + c = 0, we have a = 3, b = 0, and c = 7.
Note that a and c have the same sign, since a is positive and c is positive .
We also have b = 0.
This means that -4ac will be negative = -84).
Also, b2 = 0.
So, b2 4ac will be negative .
So, the discriminant D = -84 is negative.
Example 2: Negative Discriminant
Consider the quadratic equation 5×2 + 10x + 8 = 0.
Since it has the form ax2 + bx + c = 0, we have a = 5, b = 10, and c = 8.
Note that a and c have the same sign, since a is positive and c is positive .
We also have b not equal to zero .
This means that -4ac will be negative = -160).
So, b2 4ac will be negative .
Also Check: Holt Mcdougal Geometry Worksheet Answers
Use In Algebraic Geometry
The typical use of discriminants in algebraic geometry is for studying plane algebraic curves, and more generally algebraic hypersurfaces. Let V be such a curve or hypersurface V is defined as the zero set of a multivariate polynomial. This polynomial may be considered as a univariate polynomial in one of the indeterminates, with polynomials in the other indeterminates as coefficients. The discriminant with respect to the selected indeterminate defines a hypersurface W in the space of the other indeterminates. The points of W are exactly the projection of the points of V , which either are singular or have a tangent hyperplane that is parallel to the axis of the selected indeterminate.
For example, let f be a bivariate polynomial in X and Y with real coefficients, so that f= 0 is the implicit equation of a real plane algebraic curve. Viewing f as a univariate polynomial in Y with coefficients depending on X, then the discriminant is a polynomial in X whose roots are the X-coordinates of the singular points, of the points with a tangent parallel to the Y-axis and of some of the asymptotes parallel to the Y-axis. In other words, the computation of the roots of the Y-discriminant and the X-discriminant allows one to compute all of the remarkable points of the curve, except the inflection points.
What Is Standard Form In Place Value
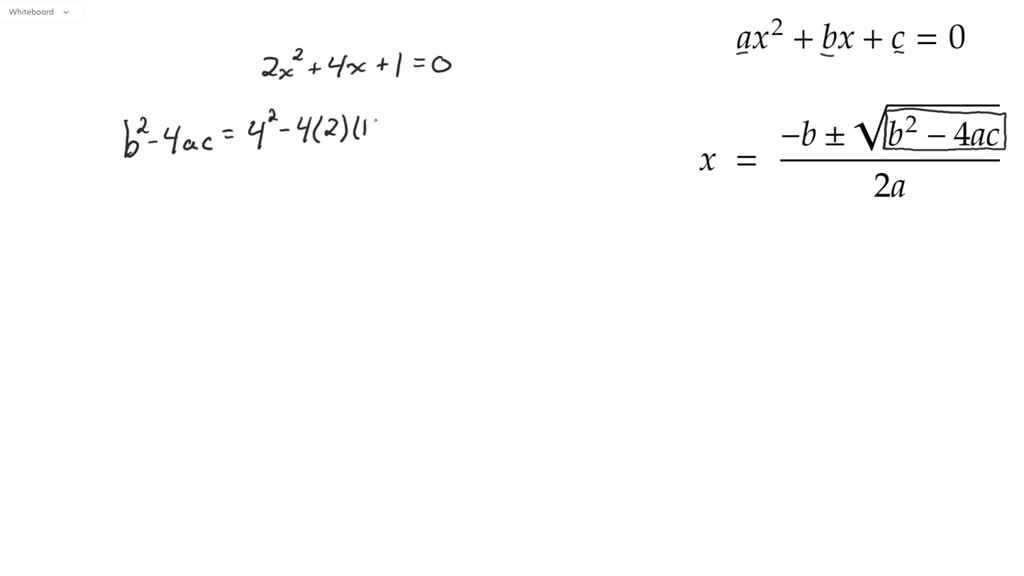
Place value is the basis of our entire number system. A place value system is one in which the position of a digit in a number determines its value. In the standard system, called base ten, each place represents ten times the value of the place to its right. In standard form, the number modeled above is 233.
Don’t Miss: Geometry Segment Addition Postulate Worksheet
Relationship Between Discriminant And Nature Of Roots
The discriminant value helps to determine the nature of the roots of the quadratic equation. The relationship between the discriminant value and the nature of roots are as follows:
- If discriminant > 0, then the roots are real and unequal
- If discriminant = 0, then the roots are real and equal
- If discriminant < 0, then the roots are not real
Example: Solve 5×2 + 6x + 1 = 0
b ± 2a6 ± 2×56 ± 106 ± 10
Try singing it a few times and it will get stuck in your head!
Or you can remember this story:
x = b ± 2a
“A negative boy was thinking yes or no about going to a party,at the party he talked to a square boy but not to the 4 awesome chicks.It was all over at 2 am.“
You May Like: What Does K Stand For In Physics
What Does The Discriminant Tell You About The Graph
4.7/5discriminantyougraphgraphgraphgraph
The discriminant tells us the following information about a quadratic equation: If the solution is a real number or an imaginary number. If the solution is rational or if it is irrational. If the solution is one unique number or two different numbers.
Likewise, why is the discriminant important? The quadratic equation discriminant is important because it tells us the number and type of solutions. This information is helpful because it serves as a double check when solving quadratic equations by any of the four methods .
One may also ask, how do you tell if a graph has a negative discriminant?
If the discriminant is negative, that means that the roots of the quadratic function are not real numbers. In other words, the graph has no x-intercepts. Of the four choices that are given, choices and are both possible. If the discriminant is negative the roots are complex.
What is a discriminant in algebra?
mathematics. Discriminant, in mathematics, a parameter of an object or system calculated as an aid to its classification or solution. In the case of a quadratic equation ax2 + bx + c = 0, the discriminant is b2 â 4ac for a cubic equation x3 + ax2 + bx + c = 0, the discriminant is a2b2 + 18abc â 4b3 â 4a3c â 27c2.
How Do You Find The Discriminant Of A Graph
4.5/5discriminantdiscriminantgraph
The discriminant is the part of the quadratic formula underneath the square root symbol: b²-4ac. The discriminant tells us whether there are two solutions, one solution, or no solutions.From the equation, we see:
Secondly, what does the discriminant tell you? The discriminant tells us the following information about a quadratic equation: If the solution is a real number or an imaginary number. If the solution is rational or if it is irrational. If the solution is one unique number or two different numbers.
Similarly one may ask, how do I find the discriminant of a parabola?
Quadratic Equations
WHAT IS A in vertex form?
The vertex form of a quadratic is given by. y = a2 + k, where is the vertex. The “a” in the vertex form is the same “a” as. in y = ax2 + bx + c . The sign on “a” tells you whether the quadratic opens up or opens down.
You May Like: Ccl4 Electron Pair Geometry
What Is A Discriminant In An Equation
Discriminant, in mathematics, a parameter of an object or system calculated as an aid to its classification or solution. In the case of a quadratic equation ax2 + bx + c = 0, the discriminant is b2 4ac for a cubic equation x3 + ax2 + bx + c = 0, the discriminant is a2b2 + 18abc 4b3 4a3c 27c2.
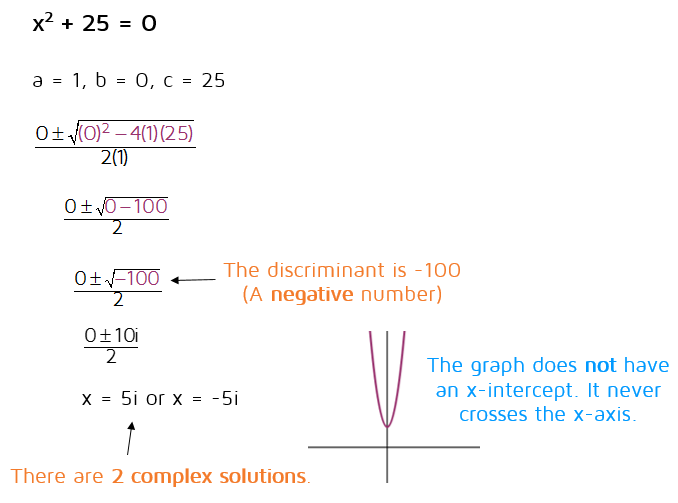
Example: Solve 5×2 + 2x + 1 = 0
Coefficients:Discriminant16
Answer: x = 2 ± 1.5i
The graph does not cross the x-axis. That is why we ended up with complex numbers.
BUT an upside-down mirror image of our equation does cross the x-axis at 2 ± 1.5 .
Just an interesting fact for you!
- Quadratic Equation in Standard Form: ax2 + bx + c = 0
- Quadratic Equations can be factored
- Quadratic Formula: x = b ± 2a
- When the Discriminant is:
- positive, there are 2 real solutions
- zero, there is one real solution
- negative, there are 2 complex solutions
Also Check: Movement Definition Geography
How Do You Use The Discriminant To Find Roots
Correct answer: b2 4ac = 2 4 = 64 64 = 0. When the discriminant is greater than 0, there are two distinct real roots. When the discriminant is equal to 0, there is exactly one real root. When the discriminant is less than zero, there are no real roots, but there are exactly two distinct imaginary roots.
Discriminant Definition In Math
The discriminant of a polynomial is a function of its coefficients which gives an idea about the nature of its roots. For a quadratic polynomial ax2 + bx + c, the formula of discriminant is given by the following equation :
D = b2 4ac
For a cubic polynomial ax3 + bx2 + cx + d, its discriminant is expressed by the following formula
D= b2c24ac34b3d27a2d2+18abcd
Similarly, for polynomials of higher degrees also, the discriminant is always a polynomial function of the coefficients. For higher degree polynomials, the discriminant equation is significantly large. The number of terms in discriminant exponentially increases with the degree of the polynomial. For a fourth-degree polynomial, the discriminant has 16 terms for fifth-degree polynomial, it has 59 terms, and for a sixth-degree polynomial, there are 246 terms.
Also, learn:
You May Like: Angle Addition Postulate Worksheet Answers
How Do You Find The Discriminant In Math
How do you find the discriminant in math? Discriminant, in mathematics, a parameter of an object or system calculated as an aid to its classification or solution. In the case of a quadratic equation ax2 + bx + c = 0, the discriminant is b2 4ac for a cubic equation x3 + ax2 + bx + c = 0, the discriminant is a2b2 + 18abc 4b3 4a3c 27c2.
How do you find the discriminant of two variables? In two variables, the general quadratic equation is ax2 + bxy + cy2 + dx + ey + f = 0, in which a, b, c, d, e, and f are arbitrary constants and a, c 0. The discriminant and the invariant together provide information as to the shape of the curve.
What happens if the discriminant is positive? A positive discriminant indicates that the quadratic has two distinct real number solutions. A discriminant of zero indicates that the quadratic has a repeated real number solution. A negative discriminant indicates that neither of the solutions are real numbers.
What does it mean if the discriminant is negative? The discriminant is the term underneath the square root in the quadratic formula and tells us the number of solutions to a quadratic equation. If the discriminant is positive, we know that we have 2 solutions. If it is negative, there are no solutions and if the discriminant is equal to zero, we have one solution.
Discriminants And Determining The Number Of Real Roots Of A Quadratic Equation
What is a discriminant?
A discriminant is a value calculated from a quadratic equation. It use it to ‘discriminate’ between the roots of a quadratic equation.
A quadratic equation is one of the form: ax2 + bx + c
The discriminant, D = b2 – 4ac
Note: This is the expression inside the square root of the quadratic formula
There are three cases for the discriminant
b2 – 4ac > 0
If the discriminant is greater than zero, this means that the quadratic equation has two real, distinct roots.
a = 1, b = -5, c = 2
Therefore, there are two real, distinct roots to the quadratic equation
x2 – 5x + 2.
b2 – 4ac < 0
If the discriminant is greater than zero, this means that the quadratic equation has no real roots.
a = 3, b = 2, c = 1
Therefore, there are no real roots to the quadratic equation 3×2 + 2x + 1.
b2 – 4ac = 0
If the discriminant is equal to zero, this means that the quadratic equation has two real, identical roots.
a = 1, b = 2, c = 1
Therefore, there are two real, identical roots to the quadratic equation x2 + 2x + 1.
Quadratic equation is ax2 + bx + c
Determinant D = b2 – 4ac
D > 0 means two real, distinct roots.
D = 0 means two real, identical roots/
D < 0 means no real roots.
Now try these,
Q1. x2 – 7x + 2 = 0
Q2. – 3×2 + 2x – 1 = 0
Q3. 9×2 – 12x + 4 = 0
Q4. – x2 + x + 1 = 0
Q1. D = 41, means two real, distinct roots.
Q2. D = -16, means no real roots.
Q3. D = 0, means two real, identical roots.
Q4. D = 5, means two real, distinct roots.
160329 Views
Also Check: What Is The Value Of The Bond Angles In Ccl4
What Is A Discriminant In Algebra 2
4.3/5Discriminant
The discriminant is the part of the quadratic formula underneath the square root symbol: b²-4ac. The discriminant tells us whether there are two solutions, one solution, or no solutions.
Secondly, how does the discriminant work? The discriminant is the expression b2 – 4ac, which is defined for any quadratic equation ax2 + bx + c = 0. If you get 0, the quadratic will have exactly one solution, a double root. If you get a negative number, the quadratic will have no real solutions, just two imaginary ones.
In this way, how do you find the discriminant of two variables?
In two variables, the general quadratic equation is ax2 + bxy + cy2 + dx + ey + f = 0, in which a, b, c, d, e, and f are arbitrary constants and a, c 0. The discriminant and the invariant together provide information as to the shape of the curve.
What does the discriminant tell you?
The discriminant tells us the following information about a quadratic equation: If the solution is a real number or an imaginary number. If the solution is rational or if it is irrational. If the solution is one unique number or two different numbers.
What Happens If The Discriminant Is Greater Than 0
When the discriminant is greater than 0, there are two distinct real roots. When the discriminant is equal to 0, there is exactly one real root. When the discriminant is less than zero, there are no real roots, but there are exactly two distinct imaginary roots. In this case, there is exactly one real root.
Recommended Reading: Age Math Word Problems
What Does B 2 4ac Tell You
Quadratic Polynomials
The quantity b24ac is called the discriminant of the polynomial. If b24ac < 0 the equation has no real number solutions, but it does have complex solutions. If b24ac = 0 the equation has a repeated real number root. If b24ac > 0 the equation has two distinct real number roots.
All Signs Point To The Discriminant
Algebra
Have you ever owned one of those Magic 8 Balls? They look like comically oversized pool balls, but have a flat window built into them, so that you can see what’s insidea 20-sided die floating in disgusting opaque blue goo. Supposedly, the billiard ball has prognostic powers all you have to do is ask it a question, give it a shake, and slowly, mystically, like a petroleum-covered seal emerging from an oil spill, the die will rise to the little window and reveal the answer to your question.
The quadratic equation contains a Magic 8 Ball of sorts. The expression b2 – 4ac from beneath the radical sign is called the discriminant, and it can actually determine for you how many solutions a given quadratic equation has, if you don’t feel like actually calculating them. Considering that an unfactorable quadratic equation requires a lot of work to solve , it’s often useful to gaze into the mystic beyond to make sure the equation even has any real number solutions before you spend any time actually trying to find them.
Talk the Talk
The discriminant is the expression b2 – 4ac, which is defined for any quadratic equation ax2 + bx + c = 0. Based upon the sign of the expression, you can determine how many real number solutions the quadratic equation has.
Here’s how the discriminant works. Given a quadratic equation ax2 + bx + c = 0, plug the coefficients into the expression b2 – 4ac to see what results:
- 3x2 – 2x + 1= 0
See also:
Don’t Miss: Geometry Segment Addition Postulate Worksheet