Math: How To Find The Derivative Of A Function
I studied applied mathematics, in which I did both a bachelor’s and a master’s degree.
The derivative of a function f is an expression that tells you what the slope of f is in any point in the domain of f. The derivative of f is a function itself. In this article, we will focus on functions of one variable, which we will call x. However, when there are more variables, it works exactly the same. You can only take the derivative of a function with respect to one variable, so then you have to treat the other variable as a constant.
Example: The Function F = X2
We know f = x2, and we can calculate f :
| Start with: |
| f = x2 + 2x x + 2 |
f fxffx2 + 2x x + 2 x2x2x x + 2xas x heads towards 0
Result: the derivative of x2 is 2x
In other words, the slope at x is 2x
We write dx instead of “x heads towards 0”.
And “the derivative of” is commonly written ddx like this:
ddxx2 = 2x“The derivative of x2 equals 2x“or simply “d dx of x2 equals 2x“
The Derivative As A Rate Of Change
Suppose $$D$$ represents a runner’s distance from the starting line. Then, the derivative of $$D$$ is given by
$$D’ = \lim_\frac$$
Without the limit, the fraction represents
$$ \begin \frac & = \frac}}\\& = \frac}}\\& = \mbox\\& = \mbox \end $$
As we apply the limit, the time elapsed approaches zero. The value of the limit is therefore the velocity at a particular time. This is still a rate of change, but now it is instantaneous.
Example 3
Suppose a runner’s distance from the starting line can be described by the function $$D = 10\sqrt + 5$$ for all values of $$t\in$$, where $$t$$ is in seconds and distance is in meters. What is the runner’s velocity at $$t = 9$$?
Since $$D = 10t^ + 5$$ we have
$$ D’ = 5t^ = \frac 5 $$
$$ D’ = \frac 5 = \frac 5 3 $$
Interpret the numerical value.
Since the derivative is positive, we know the function is increasing. That means the runner’s distance from the start line is increasing, so the runner is moving away from the start line.
The value of the derivative tells us how fast the runner is moving. The sign of the derivative tells us in what direction the runner is moving.
After 9 seconds, the runner is moving away from the start line at a rate of $$\frac 5 3\approx 1.67$$ meters per second.
Example 4
Suppose $$B$$ represents the number of books sold at a bookstore during the $$t^$$ hour of business. What does the equation $$B’ = 25$$ mean in terms of sales and time?
Identify the units of the derivative.
$$ B’ = \frac = \frac}} = \frac}} $$
Read Also: How To Do Elimination In Math
The Derivative Tells Us About Rates Of Change
Example 1
Suppose $$D$$ is a function that measures our distance from home as a function of time .
Then $$D = 5$$ means you are 5 miles from home after 2 hours have elapsed,
and $$D’ = 20$$ tells us that after 2 hours have elapsed…
$$ \frac}} = \frac}} = 20\mbox $$
So $$D’ = 20$$ is telling us that after 2 hours have elapsed our velocity is 20 miles per hour.
Example 2
Suppose $$C$$ is the cost of producing $$x$$ tons of macaroni.
Then $$C = 15000$$ tells us that producing 30 tons of macaroni will cost $15,000,
and $$C’ = 48000$$ tells us that when we are producing 30 tons of macaroni, the associated costs are increasing at a rate of $48,000 per ton.
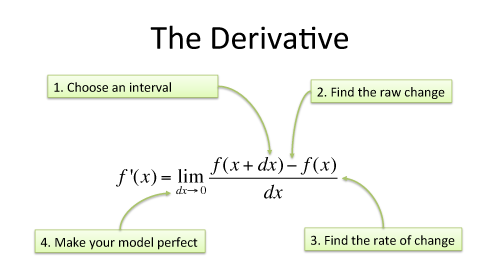
The Definition Of The Derivative
Cornell UniversityPhD. in Mathematics
Norm was 4th at the 2004 USA Weightlifting Nationals! He still trains and competes occasionally, despite his busy schedule.
The definition of the derivative is the slope of a line that lies tangent to the curve at the specific point. The limit of the instantaneous rate of change of the function as the time between measurements decreases to zero is an alternate derivative definition. The derivative is a function, and derivatives of many kinds of functions can be found, including linear, power, polynomial, exponential, and logarithmic functions.
You May Like: Define Figure Ground In Psychology
Webster Dictionaryrate This Definition:
Derivativeadjective
obtained by derivation derived not radical, original, or fundamental originating, deduced, or formed from something else secondary as, a derivative conveyance a derivative word
Etymology:
Derivativenoun
that which is derived anything obtained or deduced from another
Etymology:
Derivativenoun
a word formed from another word, by a prefix or suffix, an internal modification, or some other change a word which takes its origin from a root
Etymology:
Derivativenoun
a chord, not fundamental, but obtained from another by inversion or, vice versa, a ground tone or root implied in its harmonics in an actual chord
Etymology:
Derivativenoun
an agent which is adapted to produce a derivation
Etymology:
Derivativenoun
a derived function a function obtained from a given function by a certain algebraic process
Etymology:
Derivativenoun
a substance so related to another substance by modification or partial substitution as to be regarded as derived from it thus, the amido compounds are derivatives of ammonia, and the hydrocarbons are derivatives of methane, benzene, etc
Etymology:
The Derivative As The Slope Of A Tangent Line
Recall that the definition of the derivative is
$$ \displaystyle\lim_ \frac. $$
Without the limit, this fraction computes the slope of the line connecting two points on the function .
The only thing the limit does is to move the two points closer to each other until they are right on top of each other. But the fundamental calculation is still a slope. So the end result is the slope of the line that is tangent to the curve at the point $$)$$.
Example 1
Suppose $$f = 5x^3 – 8x$$. Determine the slope of the tangent line at $$x = 1$$.
$$ f’ = 15^2 – 8 = 7 $$
The tangent line at $$x = 1$$ has a slope of $$m = 7$$.
You May Like: Segment Addition Postulate Practice Answer Key
Princeton’s Wordnetrate This Definition:
derived function, derivative, differential coefficient, differential, first derivativenoun
the result of mathematical differentiation the instantaneous change of one quantity relative to another df/dx
derivativenoun
a compound obtained from, or regarded as derived from, another compound
derivative instrument, derivativenoun
a financial instrument whose value is based on another security
derivativeadjective
a word that is derived from another word
“`electricity’ is a derivative of `electric'”
derivativeadjective
resulting from or employing derivation
“a derivative process” “a highly derivative prose style”
The Derivative Is A Function
Suppose we have a particular function:
$$f =2x^5+7x^3+5$$
Through a process called differentiation1 we can find another function that’s related to $$f$$. This second function is called the derivative of $$f$$. For this example, the derivative is:
$$f’ = 10x^4 + 21x^2$$
1Differentiation means finding the derivative.
Also Check: What Is The Molecular Geometry Of Ccl4
What Does It Mean For A Function To Be Differentiable
A differentiable function is one you can differentiate…. everywhere!
That sounds a bit like a dictionary definition, doesn’t it? Completely accurate, but not very helpful!But, if you explore this idea a little further, you’ll find that it tells you exactly what “differentiable means”.
Differentiable functions are nice, smooth curvy animals. They have no gaps or pointy bits.
Multiple Applications In Math And Physics
The derivative is a function that gives the slope of a function in any point of the domain. It can be calculated using the formal definition, but most times it is much easier to use the standard rules and known derivatives to find the derivative of the function you have.
Derivatives have a lot of applications in math, physics and other exact sciences.
This content is accurate and true to the best of the authorâs knowledge and is not meant to substitute for formal and individualized advice from a qualified professional.
Read Also: How Do You Do Elimination In Math
What Is The Upside Down Triangle Symbol In Math
Answer itupside down trianglenumber
Similarly, it is asked, what is the meaning of an upside down triangle?
trianglerepresenttrianglemeanupside down triangletriangle
What is the name of an upside down triangle?
upside down triangle
What does an upside down pink triangle mean?
Pink Trianglepink triangle
So What Does Ddxx2 = 2x Mean
It means that, for the function x2, the slope or “rate of change” at any point is 2x.
So when x=2 the slope is 2x = 4, as shown here:
Or when x=5 the slope is 2x = 10, and so on.
Note: f can also be used for “the derivative of”:
f = 2x“The derivative of f equals 2x”or simply “f-dash of x equals 2x”
We know f = x3, and can calculate f :
| Start with: |
| f = x3 + 3×2 x + 3x 2 + 3 |
f fxffx3 + 3×2 x + 3x 2 + 3 x3x3×2 x + 3x 2 + 3xas x heads towards 0
Result: the derivative of x3 is 3×2
Have a play with it using the Derivative Plotter.
Also Check: Eoc Fsa Warm Ups Algebra 1 Answers
Rules For Basic Functions
Here are the rules for the derivatives of the most common basic functions, where a is a real number.
- x . f’& =4x^+\right)}}\cos \left-\right)}}e^-\ln\right)}}+0\\& =4x^+2x\cos \left-}e^-\lne^.\end}}
Here the second term was computed using the chain rule and third using the product rule. The known derivatives of the elementary functions x2, x4, sin, ln and exp = ex, as well as the constant 7, were also used.
The Geometrical Concept Of The Derivative
yfxf
Fix a point on the graph, say ). If the graph as ageometric figure is “nice” around this point, it isnatural to ask whether one can find the equation of the straightline “touching” the graph at that point. Such a straight line iscalled the tangent line at the point in question. Theconcept of tangent may be viewed in a more general framework.
One way to find the tangent line is to considerpoints ) on the graph, where x is very close tox0. Then draw the straight-line joining both points :
As you can see, when x get closer and closer to x0, thelines get closer and closer to the tangent line. Since all theselines pass through the point ), their equations willbe determined by finding their slope: The slope of the linepassing through the points ) and ) is given by
mmxx
In other words, we have
Notation. Writing “m” for the slope of the tangent linedoes not carry enough information we want to keep track of thefunction f and the point x0 in our notation. The commonnotation used is
mfyffhxx
Read Also: Eric Van Wilderman Geometry Dash
Derivative As A Function
Let f be a function that has a derivative at every point in its domain. We can then define a function that maps every point x to the value of the derivative of f at x. This function is written fâ² and is called the derivative function or the derivative off.
Sometimes f has a derivative at most, but not all, points of its domain. The function whose value at a equals fâ² whenever fâ² is defined and elsewhere is undefined is also called the derivative of f. It is still a function, but its domain is strictly smaller than the domain of f.
Using this idea, differentiation becomes a function of functions: The derivative is an operator whose domain is the set of all functions that have derivatives at every point of their domain and whose range is a set of functions. If we denote this operator by D, then D is the function fâ². Since D is a function, it can be evaluated at a point a. By the definition of the derivative function, D = fâ².
For comparison, consider the doubling function given by f = 2x f is a real-valued function of a real number, meaning that it takes numbers as inputs and has numbers as outputs:
- 1
- ) . D& =,\\D& =,\\D\left& =.\end}}
Because the output of D is a function, the output of D can be evaluated at a point. For instance, when D is applied to the square function, x ⦠x2, D outputs the doubling function x ⦠2x, which we named f. This output function can then be evaluated to get f = 2, f = 4, and so on.
The Derivative As A Function
- Publisher: OpenStax CNX
- Define the derivative function of a given function.
- Graph a derivative function from the graph of a given function.
- State the connection between derivatives and continuity.
- Describe three conditions for when a function does not have a derivative.
- Explain the meaning of a higher-order derivative.
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. In this section we define the derivative function and learn a process for finding it.
You May Like: Countdown To The Algebra 1 Eoc Answer Key
Definition Of The Derivative
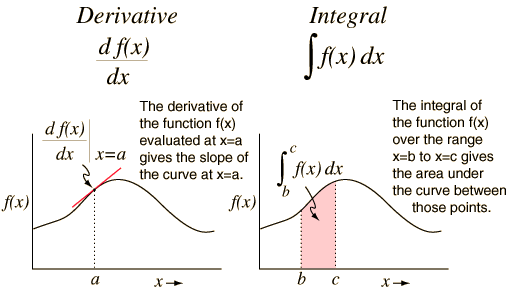
The derivative of a function is one of the basic concepts of mathematics. Together with the integral, derivative occupies a central place in calculus. The process of finding the derivative is called differentiation. The inverse operation for differentiation is called integration.
The derivative of a function at some point characterizes the rate of change of the function at this point. We can estimate the rate of change by calculating the ratio of change of the function \ to the change of the independent variable \. In the definition of derivative, this ratio is considered in the limit as \ Let us turn to a more rigorous formulation.
The Derivative Is The Exact Rate At Which One Quantity Changes With Respect To Another In Calculus We Have Learned That When Y Is The Function Of X The Derivative Of Y With Respect To X Ie Dy/dx Measures The Rate Of Change In Y With Respect To X Geometrically The Derivatives Are The Slope Of The Curve At A Point On The Curve The Derivative Is Often Called The Instantaneous Rate Of Change In The Next Few Paragraphs We Will Take A Deep Dig Into The Application Of Derivatives In Real Life
The derivative of a function represents an infinitely small change in the function with respect to one of its variations. The process of finding the derivatives is called differentiation. Modern differentiation and derivatives are usually credited to Sir Issac Newton and Gottfried Leibniz. They developed the fundamental theorem of calculus in the 17th century. This related differentiation and integration in ways that revolutionized the methods for computing areas and volumes. However, Newtons work would not have been possible without the efforts of Issac Brown who began the early development of the derivative in the 16th century.
The bottom line is that nothing is useless. Whenever we say something is useless, it simply means that we dont know how to use them. but I will bet somewhere someone knows how to use it.
And derivatives, which is the mathematical model of change and has amazing prediction powers, is extremely useful in our everyday life. You would need some practice to know how to use it well in everyday life. But once you master it, it helps greatly to weed out irrationality, clarify your choices, and helps in forecasting.
Through derivatives, we can easily find out the maximum and minimum values of particular functions and find whether the function is increasing or decreasing. There are countless areas where derivatives can be used.
Here are the most important areas where derivatives are used.
Read Also: Chapter Test B Geometry Answers
Formal Definition Of The Derivative
Let \\) be a function whose domain contains an open interval about some point \. Then the function \\) is said to be differentiable at \, and the derivative of \\) at \ is given by
Lagrange’s notation is to write the derivative of the function \\) as \\) or \.\)
Leibniz’s notation is to write the derivative of the function \\) as \ or \
The steps to find the derivative of a function \\) at the point \ are as follows:
- Form the difference quotient \ – f\left}}}\)
- Simplify the quotient, canceling \ if possible
- Find the derivative \\), applying the limit to the quotient. If this limit exists, then we say that the function \\) is differentiable at \.
Next, we derive the derivatives of the basic elementary functions using the formal definition of derivative. These functions comprise the backbone in the sense that the derivatives of other functions can be derived from them using the basic differentiation rules.
Making The Definition More Precise

Most of the above definition is perfectly acceptable. The only thing we really need to nail down is what we mean by “everywhere”. Does this meanthat we take the function on a trip, and try to differentiate it at every place we visit? Of course not! What we mean is that we can evaluate its derivativeat every value of \ that we can input into the function definition. There’s a technical term for these \-values:
Read Also: Practice 2-4 Reasoning In Algebra Answers