What Does Particle Number Conservation Mean In Condensed Matter Physics
Conservation of the number of particle is a symmetry of the system. As Akshay Kumar said in his response, when the number of particles operator commutes with the Hamiltonian, it is conserved. It simply means, well, that’s the number of particle is conserved. Particles are all what is discussed in condensed matter , like electrons and holes . So it should be fine to know if some particles can or not pop-out from nowhere. Fortunately enough, when the particle number is conserved, they do not pop-out from nowhere, they can only be transmuted from an other particle. That’s what happens with superconductivity: two electrons disappear and one Cooper pair emerges .
Now for superconductivity, it is easier to say that you will conserve the number of particles if your Hamiltonian is invariant with respect to the transformation
$$c\rightarrow e^\theta}c$$ and $$c^\rightarrow e^\theta}c^$$
where the $c$’s are the fermionic operators, and $\theta$ an angle. Actually, $\theta$ is better defined as the generator of the U rotation. In particular, if your Hamiltonian is invariant with the phase shift operation defined above, you can associated a Noether current to it. For the U rotation symmetry, the conserved current will be the current of particles. In particular for time independent problems , the number of particles will be conserved if your Hamiltonian is invariant under the above defined transformation.
$$H_}\propto c^c^cc$$
Conservation Of Energy In Beta Decay
The discovery in 1911 that electrons emitted in beta decay have a continuous rather than a discrete spectrum appeared to contradict conservation of energy, under the then-current assumption that beta decay is the simple emission of an electron from a nucleus. This problem was eventually resolved in 1933 by Enrico Fermi who proposed the correct description of beta-decay as the emission of both an electron and an antineutrino, which carries away the apparently missing energy.
Conservation Laws As Fundamental Laws Of Nature
Conservation laws are fundamental to our understanding of the physical world, in that they describe which processes can or cannot occur in nature. For example, the conservation law of energy states that the total quantity of energy in an isolated system does not change, though it may change form. In general, the total quantity of the property governed by that law remains unchanged during physical processes. With respect to classical physics, conservation laws include conservation of energy, mass , linear momentum, angular momentum, and electric charge. With respect to particle physics, particles cannot be created or destroyed except in pairs, where one is ordinary and the other is an antiparticle. With respect to symmetries and invariance principles, three special conservation laws have been described, associated with inversion or reversal of space, time, and charge.
Conservation laws are considered to be fundamental laws of nature, with broad application in physics, as well as in other fields such as chemistry, biology, geology, and engineering.
Most conservation laws are exact, or absolute, in the sense that they apply to all possible processes. Some conservation laws are partial, in that they hold for some processes but not for others.
Also Check: What Is Agriculture In Geography
What Is Conservation Of Energy
Physics has discovered over the years that there are several forms of energy. These energies can be transferred from one system to another in certain ways. This conclusion leads to two main energy types mechanical energy, which is a total of kinetic and potential energy and the energy transferred through work done by neoconservative forces, Wnc.
Energy can neither be created nor destroyed. It can just be transformed from one form into another.”
We can see the conservation of energy in our everyday lives. For instance, a generator converts mechanical energy into electrical energy. But for practical generators, there seems to always be a difference between the energy input and output. So if the energy is conserved, where does this lost energy go? In this instance, the ‘lost’ energy is mainly converted into unwanted thermal energy in the form of heat.
Solar panels are a great everyday example of energy forms transforming into each other, since the solar panels convert light energy from the sun into electrical energy.
You have learned that there are many forms of energy. We will study energy in the forms of kinetic energy, potential energy, and work done by nonconservative forces. Let’s gather the rest in a group which we will call other energy, or OE.
We are going to focus on circumstances where OE is constant, hence it will not be considered and will be subtracted out.
Law Of Conservation Of Energy
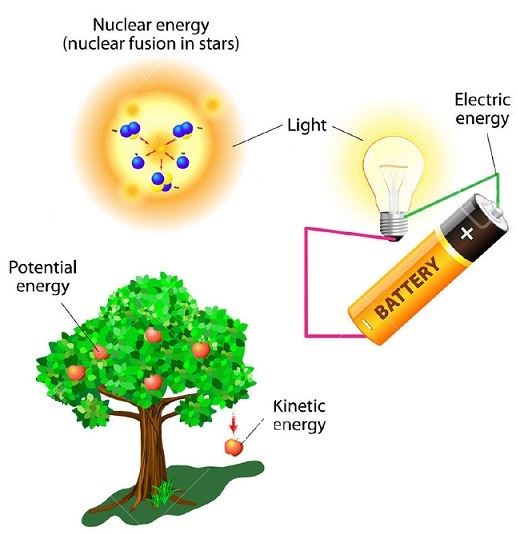
“Energy cannot be created or destroyed… it can only be changed.”
Chances are you’ve heard that phrase before. it’s one of the most important concepts in all of physics. It doesn’t mean that an object can’t lose energy or gain energy… what it means is that energy can be changed into different forms, and transferred from system to system, but it never magically disappears or reappears.
Following up on our bank account analogy, if you have a certain amount of money in your bank account, if you spend some money, your bank account balance decreases. Your money wasn’t lost, however, it was transferred to another system. It may even change forms… perhaps you purchased an item from another country. Your money is no longer in the form of dollars and cents, but is instead now part of another system in another currency.
There are some issues with our money analogy, however. If the total money supply in a country is low, a government can print more currency. In the world of physics, however, the total amount of energy throughout the universe is fixed… it cannot be replenished. Alternately, governments can collect and destroy currency — in the world of physics, we can never truly destroy energy. The understanding that the total amount of energy in the universe remains fixed is known as the law of conservation of energy.
Recommended Reading: How Is Math Used In Pediatrics
What Happens When Kinetic Energy Is Not Conserved
Elastic collisions are collisions in which both momentum and kinetic energy are conserved. The total system kinetic energy before the collision equals the total system kinetic energy after the collision. If total kinetic energy is not conserved then the collision is referred to as an inelastic collision.
Introduction To Conservation Of Momentum
Likewise, with the other conservation standards, there is a catch: conservation of momentum applies just to an object of an isolated system. For this situation, an isolated system is one that is not acted on by any external force to the system i.e., there is no external impulse. Practically this means we need to incorporate the two objects and anything that applies a force to any of the objects for any timeframe in the system.
On the off chance, if i and f indicate the initial and final momentum of objects in a framework, then the principle of conservation of momentum says that
Also Check: Lesson 4.9 Practice B Geometry Answers
Global And Local Conservation Laws
The total amount of some conserved quantity in the universe could remain unchanged if an equal amount were to appear at one point A and simultaneously disappear from another separate point B. For example, an amount of energy could appear on Earth without changing the total amount in the Universe if the same amount of energy were to disappear from some other region of the Universe. This weak form of “global” conservation is really not a conservation law because it is not Lorentz invariant, so phenomena like the above do not occur in nature. Due to special relativity, if the appearance of the energy at A and disappearance of the energy at B are simultaneous in one inertial reference frame, they will not be simultaneous in other inertial reference frames moving with respect to the first. In a moving frame one will occur before the other either the energy at A will appear before or after the energy at B disappears. In both cases, during the interval energy will not be conserved.
Mechanical Equivalent Of Heat
A key stage in the development of the modern conservation principle was the demonstration of the mechanical equivalent of heat. The caloric theory maintained that heat could neither be created nor destroyed, whereas conservation of energy entails the contrary principle that heat and mechanical work are interchangeable.
In the middle of the eighteenth century, Mikhail Lomonosov, a Russian scientist, postulated his corpusculo-kinetic theory of heat, which rejected the idea of a caloric. Through the results of empirical studies, Lomonosov came to the conclusion that heat was not transferred through the particles of the caloric fluid.
In 1798, Count Rumford performed measurements of the frictional heat generated in boring cannons, and developed the idea that heat is a form of kinetic energy his measurements refuted caloric theory, but were imprecise enough to leave room for doubt.
The mechanical equivalence principle was first stated in its modern form by the German surgeon in 1842. Mayer reached his conclusion on a voyage to the Dutch East Indies, where he found that his patients’ blood was a deeper red because they were consuming less oxygen, and therefore less energy, to maintain their body temperature in the hotter climate. He discovered that heat and mechanical work were both forms of energy and in 1845, after improving his knowledge of physics, he published a monograph that stated a quantitative relationship between them.
Recommended Reading: Glencoe Mcgraw Hill Geometry Workbook Answers
Conservation Of Angular Momentum
The angular momentum of an isolated system remains constant in both magnitude and direction. The angular momentum is defined as the product of the moment of inertia I and the angular velocity. The angular momentum is a vector quantity and the vector sum of the angular momenta of the parts of an isolated system is constant. This puts a strong constraint on the types of rotational motions which can occur in an isolated system. If one part of the system is given an angular momentum in a given direction, then some other part or parts of the system must simultaneously be given exactly the same angular momentum in the opposite direction. As far as we can tell, conservation of angular momentum is an absolute symmetry of nature. That is, we do not know of anything in nature that violates it.
Derivation Of Conservation Of Momentum
In the event that, if no external force is applied on the arrangement of two colliding objects. The objects apply impulse on one another for a short timespan at the point of contact. As per Newtons third law of motion, the impulsive force applied by the first object on the second one is equal and opposite to the impulsive force applied by the second object on the first object.
Crashes are especially fascinating to dissect utilizing the conservation of momentum. This is on the grounds that collisions happen quickly. So, the time impacting objects spend connecting is short. A short association time implies that the impulse, \ \, because of external forces. Like, friction during the collision is very small.
During the one-dimensional collision of two objects of masses \ and \, which have velocities \ and \ before collision and velocities \ and \ after the collision, the impulsive force on the first object is \ and the impulsive force on the second object is \ . By applying Newtons third law, the two impulsive forces are equal and
opposite. So, \
If the time span of the contact is t, the impulse of the force \ is equal to the change in momentum of the first object.
The impulse of force \ is equal to the momentum of the second object.
From \
This relation shows that momentum is conserved during the collision.
You May Like: Who Are Paris Jackson’s Biological Parents
Energy Balance For The Gas Flowing Through The Catalyst Bed
The derivation of the energy equation for the catalyst bed follows a procedure very similar to that used in Section 3.9 to derive the energy equation for a pipe carrying a fluid. It is somewhat more complicated, however, because of the need to allow for both the presence of several chemical species in the inlet and outlet streams, and for heat conduction by the catalyst pellets. The intimate contact of gas with the catalyst pellets means that it is legitimate to assume that the gas and the catalyst share the same temperature at any given distance through the bed.
Heat conduction follows Fourier’s law, namely that the heat passed along the bed in the x-direction, x , is proportional to the temperature gradient and to the cross-sectional area:
David J. Kukulka, Rick Smith, in, 2011
What Is A Conserved Quantity Of Dynamical System
Unsourced material may be challenged and removed. In mathematics, a conserved quantity of a dynamical system is a function of the dependent variables the value of which remains constant along each trajectory of the system.
What is a conserved quantity in differential equations?
Differential equations. For a first order system of differential equations where bold indicates vector quantities, a scalar-valued function H is a conserved quantity of the system if, for all time and initial conditions in some specific domain, Note that by using the multivariate chain rule , so that the definition may be written
What is the principle of Conservation of energy?
What is the principle of conservation of energy? In physics, the term conservation refers to something which doesnt change. This means that the variable in an equation which represents a conserved quantity is constant over time.
Also Check: What Do Sex Dreams Mean Psychology
What Physical Quantities Are Conserved In An Interaction
The six conservation laws that we have encountered thus farenergy, charge, angu- lar momentum, linear momentum, baryon number, and lepton numberapply to all four of the fundamental interactions.
What is conserved quantity give an example?
What are conserved quantities and conserved laws?
In all of physics there are only six conservation laws. Each describes a quantity that is conserved, that is, the total amount is the same before and after something occurs. These laws have the restriction that the system is closed, that is, the system is not affected by anything outside it.
Faqs On Conservation Of Momentum
Q.1. What does the law of conservation of momentum state?
Answer: The law of conservation of momentum states that in an isolated system the total momentum of two or more bodies acting upon each other remains constant unless an external force is applied. Therefore, momentum can neither be created nor destroyed.
Q.2. Give Examples of Conservation of Momentum.
Answer: All physical processes abide by the law of conservation of momentum. Some examples are,
Collision: The collision of different objects follows the conservation of momentum and energy.
Rocket motion: The momentum of the gas particles ejected gives the rocket an opposite momentum. This is due to momentum conservation.
Ejection of a bullet from a gun: It is a consequence of conservation of momentum as if a gun experiences a recoil momentum due to the ejection of a bullet.
Q.3. The law of conservation of momentum is based on which law of motion?
Answer: The law of conservation of momentum is based on Newtons third law of motion. This states that every force has a reciprocating equal and opposite force.
Q.4. What is the law of conservation of momentum formula?
Answer: The momentum observation principle can be mathematically represented as:\In the equation, \ and \ are masses of the bodies, \ and \ are the initial velocities of the body. \ and \ are the final velocities of the bodies.
Q.5. Does friction affect the conservation of momentum?
Don’t Miss: What Does Concentration Mean In Geography
What Does Conservation Of Momentum Mean In Quantum Mechanics
In quantum mechanics why do we say that momentum in conserved when different measurements on particle give different values of it ?
For example in ground state of Harmonic oscillator I know that expectation value of momentum is independent of time but that is “expectation” value and not the actual momentum of particle or the momentum that we actually measure .
In quantum mechanics why do we say that momentum in conserved when different measurements on particle give different values of it ?
Italics mine.
A measurement has to happen with an interaction. Conservation laws, momentum, energy, angular momentum, imposed axiomatically so as to have continuity between quantum state measurements and macroscopic classical measurements, are in the vectorial sum of the momenta of the individual particles involved in the interaction. Sum before should equal sum after the interaction, exactly as in classical mechanics.
This axiomatic assumption has been tested implicitly with innumerable experiments and no violations have been reported by experiments.
If momentum is conserved , then what momentum conservation guarantees is that if you start the system in a momentum eigenstate, it will always remain in a momentum eigenstate .
- $\begingroup$It can also be in a superposition of momentum eigenstate and in this case not only the phase will change over time.$\endgroup$Oct 18, 2021 at 6:17
- $\begingroup$@NicolasSchmid Correct.$\endgroup$
$$\frac = 0$$
Worked Example : The Roller Coaster
A roller coaster ride at an amusement park starts from rest at a height of \ \ above the ground and rapidly drops down along its track. At some point, the track does a full 360° loop which has a height of \ \, before finishing off at ground level. The roller coaster train itself with a full load of people on it has a mass of \ \.
Roller coaster
If the roller coaster and its track are frictionless, calculate:
the velocity of the roller coaster when it reaches the top of the loop
the velocity of the roller coaster at the bottom of the loop
Read Also: Algebra 2 Page 221 Answers