S Involved In Finding Hole Of A Rational Function
Let y = f be the given rational function.
Step 1 :
If it is possible, factor the polynomials which are found at the numerator and denominator.
Step 2 :
After having factored the polynomials at the numerator and denominator, we have to see, whether there is any common factor at both numerator and denominator.
Case 1 :
If there is no common factor at both numerator and denominator, there is no hole for the rational function.
Case 2 :
If there is a common factor at both numerator and denominator, there is a hole for the rational function.
Step 3 :
Let be the common factor found at both numerator and denominator.
Now we have to make equal to zero.
When we do so, we get
x – a = 0
So, there is a hole at x = a.
Step 4 :
Let y = b for x = a.
So, the hole will appear on the graph at the point .
Philosophy And Psychology Of Holes
It has been noted that holes occupy an unusual ontological position in human psychology, as people tend to refer to them as tangible and countable objects, when in fact they are the absence of something in another object. An example of this reasoning can be found in the Beatles lyric from the song, “A Day in the Life“, from their 1967 album Sgt. Pepper’s Lonely Hearts Club Band:
I read the news today, oh boy:Four thousand holes in Blackburn Lancashire.And though the holes were rather small,They had to count them all,Now they know how many holes it takes to fill the Albert Hall.
Some people have an aversion to the sight of irregular patterns or clusters of small holes, a condition called trypophobia. Researchers hypothesize that this is the result of a biological revulsion that associates trypophobic shapes with danger or disease, and may therefore have an evolutionary basis.
A Lesson In Indigenous Traditional Math
Teddy, Leland and father Bryan Bellefeuille in colourful regalia. Bellefeuille presented traditional Indigenous math for children during an Ontario Science Centre virtual event. Photo supplied.
NIPISSING FIRST NATION Math is neat and involved in everyday life says cheery teacher Bryan Bellefeuille.
A member of Nipissing of First Nation, Bellefeuille is an Ojibwe Language teacher working for the Algoma District School Board. His job also involves integrating Indigenous knowledge into the existing Ontario Curriculum he says, to help other teachers involve and include more Indigenous knowledge into their existing lessons in the classroom.
Bellefeuille illuminated traditional math during a virtual lesson for the Ontario Science Centre on Sept. 22 for children 6 12 years old.
The engaging teacher is a firekeeper, grass dancer, and fisherman. Speaking from Mississauga #8 First Nation, he explains how math is neat.
It can be flexible and conceptual in applied situations where you are articulating the relationship between the bow and arrow when its bending and we have pressures of force at work of trying to obtain a goal of eventually hunting and getting an animal.
Bellefeuille used woven baskets constructed by Indigenous people to talk about volume and capacity.
Bellefeuille showed the intent of design in traditional objects.
Bellefeuille informed students across the globe that Indigenous people have always used math.
Don’t Miss: Blanket Jackson Biological Father
But What Does It Mean For Maths
Although Friedman’s approaches are promising, it may be a very long time until we know just how far-reaching they are. As he himself concedes, “The extent to which we have concrete incompleteness and what the wider implications are, will not be clear for hundreds of years, if not longer.”
But what will happen when undecidable questions finally do hit the mainstream? Will mathematics collapse like a house of cards? The answer isprobably no, since there’s always the option of adding new axioms toZFC, which strengthen the system and extend our intuition. These won’t do away with undecidable statements altogether, that’sGödel’s incompleteness result, but if chosen correctly, they mightstifle some particularly prolific sources of concrete incompleteness.
Just adding new axioms to sort out your problems might feel likecheating, but there are precedents. Take, for example, a technique known as mathematicalinduction, commonly used toprove statements about all the natural numbers. The idea behind induction is simple: you first prove your statement is true forthe first natural number, 0, and then you prove that if it’s true forone natural number, it’s also true for the next one along. In thisway, the numbers succumb to your statement one by one, like a row ofdominoes.
Picking Holes In Mathematics

One thing that mathematics is equally loved and reviled for is itsdefinite nature. Some people love the unerring hand of logic, but others loathe the lack ofroom for play. But once you penetrate to the very foundations of maths,the concept of true or false becomes a lot moreslippery. The logician Kurt Gödel proved in the 1930s that if youset out proper rules for mathematics, excluding leaps of faith orintuition as admissible moves, you lose the ability to decide whethercertain statements are true or false. And this isn’t because youchose the wrong rules: for any set of rules, as long as they’restrong enough to make sense of whole number arithmetic, there will be statements you can’t prove or refute.
This is rather shocking and you may wonder why Gödel’s resulthasn’t wiped out mathematics once and for all. The answer is that,initially at least, the unprovable statements logicians came upwith were quite artificial and didn’t touch on ordinary everydaymathematics. They certainly wouldn’t come up in school homework orin the maths used to design aircraft wings. The vast majority ofmathematicians leave theselogical holes to the logicians and philosophers and get on with their work.
Also Check: What Is The Molecular Geometry Of Ccl4
Incompleteness From Finite Trees
One example is aresult Friedman proved in 1982 concerning what mathematicians calltrees. In maths a tree is a network which doesn’t contain any circularpaths. It’s made up of a collection of interlinked nodes, with only one path linking any two given nodes. See figure 1 for an example.
Trees crop up in many different contexts, including computerscience: if a computer programme makes a yes/no decision at every stepof some process, then its combined options can be presented as abinary tree . Another example is genetics, where trees are used todescribe the evolution of species. This context has actually produced some some very hard mathematical questions . So in terms of concrete incompleteness, trees are a good place tolook.
One natural question to ask is whether a given finite tree contains a smaller given tree, as illustrated in figure 3. Taking this a step further, if you’ve got a whole collection of finite trees, what are your chances that one of the bigger ones contains one of the smaller ones? Surely this chance should increase as your collection of trees gets larger? In the 1960s the American mathematician Joseph Kruskal proved a result which confirms this intuition: as long as you’ve got infinitely many finite trees in your collection, you can be sure that one of them contains another.
This result can be stated in Peano arithmetic, but as Friedman showed, its proof is beyond the capacity not only of Peano arithmetic, but also some considerably stronger systems.
How To Patch Holes In Your Math Knowledge: 3 Steps
Every math student collects knowledge gaps as they progress through school. Sometimes you dont understand a concept when it gets taught, and the class moves on before you figure it out. Sometimes you get it, but since the mastery path is a muddy slope, you quickly forget. And some key pieces are, for whatever reason, never taught at all. This year, with limited schooling due to COVID, that final case is more common than ever.
And if you understand that math is an upside-down pyramid, then you know that knowledge gaps make a very unstable foundation for future learning. They increase the likelihood of getting confused, falling behind, and slipping into a downward spiral of math avoidance. So patching holes in your math knowledge is critical. But how do you do it?
What follows is a step-by-step process for identifying and filling knowledge gaps in mathematics.
1. Identify
Step one is to identify what you dont know, back up to the earliest, easiest things that you dont have mastered, and start from there. To do this, I recommend using Khan Academys course challenges. These are like miniature final exams for Khans math courses. Theres one for every grade. You can also take the unit tests that are at the end of each major subject within these math courses.
Topics with zero or one purple bar are your knowledge gaps.
2. Understand
Being confused is normal. Work through it by using resources and making written product.
3. Master
Make Progress
Read Also: What Is The Molecular Geometry Of Ccl4
To Hold Infinity In The Palm Of Your Hand
Black Holes are indeed the stuff of science and science fiction and even the youngest schoolchild who is at all interested in STEM has heard of black holes. But did you know that scientist have never taken a real picture of a real black hole? Until now!
On April 10, 2019 an international team of around 200 scientists, going under the name of the Event Horizon Telescope team, and led by Shep Doleman, released the above picture of the black hole at the center of a galaxy called M87. M87 is itself a giant galaxy 55 million light years from Earth. The black hole at its center is indeed a genuine monster it weighs more than six and a half billion times the mass of the sun. However, the gravity that holds the black hole together is so strong that the entire black hole is about one and a half light days across about the size of our solar system!
Black holes are one of the best confirmations of Einsteins General Theory of Relativity. We think of Einstein as this affable grandfatherly figure however this theory was born out of strong scientific rivalry between the physicist Einstein and the world-famous mathematician David Hilbert. Interestingly, though Einstein formulated the theory, he did not predict black holes! Karl Schwarzschild worked out the first mathematical solution of black holes. When Einstein saw the solution he did not think it could be correct.
| 3:00 PM to 8:00 PM |
| 3:00 PM to 8:00 PM |
| 3:00 PM to 8:00 PM |
| 3:00 PM to 8:00 PM |
| 10:00 AM to 3:00 PM |
How Do You Find The Horizontal Asymptote
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
Don’t Miss: Abiotic Definition Biology
Removable Discontinuities Can Be Fixed
Removable discontinuities can be fixed by redefining the function, as shown in the following example.
Example
The function below has a removable discontinuity at $$x = 2$$. Redefine the function so that it becomes continuous at $$x=2$$.
$$f = \frac$$
The graph of the function is shown below for reference.
In order to fix the discontinuity, we need to know the $$y$$-value of the hole in the graph. To determine this, we find the value of $$\lim\limits_ f$$.
Examining the form of the limit we see
$$\displaystyle\lim_ \frac = \frac = \frac 0 0$$
The division by zero in the $$\frac 0 0$$ form tells us there is definitely a discontinuity at this point.
Next, using the techniques covered in previous lessons we can easily determine
$$\displaystyle\lim_ f = \frac 1 2$$
The limit value is also the $$y$$-value of the hole in the graph. Now we can redefine the original function in a piecewise form:
$$ \\ f = \left\ \frac, & \mbox x \neq 2\\ % \frac 1 2, & \mbox x = 2 \end \right. \\ $$
The first piece preserves the overall behavior of the function, while the second piece plugs the hole.
What We Talk About When We Talk About Holes
For Halloween, I wrote about a very scary topic: higher homotopy groups. Homotopy is an idea in topology, the field of math concerned with properties of shapes that stay the same no matter how you squish or stretch them, as long as you dont tear them or glue things together.
For Halloween, I wrote about a very scary topic: higher homotopy groups. Homotopyis an idea in topology, the field of math concerned with properties of shapes that stay the same no matter how you squish or stretch them, as long as you don’t tear them or glue things together. Both homotopy groups and the somewhat related homology groups are different ways to describe the topology of shapes using algebra. In my post, I said that homology detects holes of different dimensions. But, , what do I mean by holes of different dimensions?
Good question! I deliberately used hole as a wiggle word because there isnt a real mathematical definition of hole. But heres my short answer that is also the reason Im not an algebraic topologist. If you can put it on a necklace, it has a one-dimensional hole. If you can fill it with toothpaste, it has a two-dimensional hole. For holes of higher dimensions, youre on your own.
The Stanford Encyclopedia of Philosophy has an amusing entry about holes by Robert Casati and Achille Varzi. It starts:
Read Also: Lesson 4.5 Practice A
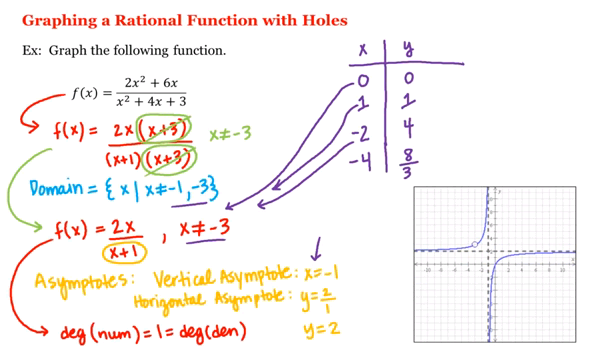
Graphing Rational Functions With Holes
A rational function is a quotient of two functions.The graph of a rational function usually has vertical asymptotes where the denominator equals 0.However, the graph of a rational function will have a hole when a value of x causes both the numerator and the denominator to equal 0. This occurs when there is a common factor in the numerator and denominator.We can set the common factor to zero and solve for x to find the hole.
The following diagram shows how to graph rational functions with holes. Scroll down the page for more examples and solutions on graphing rational functions.
Graphing rational functions with holes
Mathematical And Scientific Senses
Holes in mathematics
In mathematics, holes are examined in a number of ways. One of these is in homology, which is a general way of associating certain algebraic objects to other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology, and homology was originally a rigorous mathematical method for defining and categorizing holes in a mathematical object called a manifold. The initial motivation for defining homology groups was the observation that two shapes can be distinguished by examining their holes. For instance, a circle is not a disk because the circle has a hole through it while the disk is solid, and the ordinary sphere is not a circle because the sphere encloses a two-dimensional hole while the circle encloses a one-dimensional hole. However, because a hole is “not there”, it is not immediately obvious how to define a hole or how to distinguish different types of hole.
In geometric topology, however, holes are determined differently. In this field, the genus of a connected, orientablesurface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. In layman’s terms, it is the number of “holes” an object has . A doughnut, or torus, has 1 such hole. A sphere has 0.
Holes in physics
Holes in biology
Blind holes and through holes
There are three accepted methods of threading blind holes:
Read Also: What Does Abiotic Mean In Biology
What Is Topology
Topology studies properties of spaces that are invariant under any continuous deformation. It is sometimes called “rubber-sheet geometry” because the objects can be stretched and contracted like rubber, but cannot be broken. For example, a square can be deformed into a circle without breaking it, but a figure 8 cannot. Hence a square is topologically equivalent to a circle, but different from a figure 8.
Here are some examples of typical questions in topology: How many holes are there in an object? How can you define the holes in a torus or sphere? What is the boundary of an object? Is a space connected? Does every continuous function from the space to itself have a fixed point?Topology is a relatively new branch of mathematics most of the research in topology has been done since 1900. The following are some of the subfields of topology.
|
Torus |
Klein Bottle |
Algebraic topology sometimes uses the combinatorial structure of a space to calculate the various groups associated to that space.