A Variety Of Properties
Apart from distributive property, there are other commonly used properties such as the associative property and Commutative property.
Let’s look at the associative property:
The associative property refers to grouping elements together. This rule states that how numbers are grouped within a math problem will not change the product.
Example in addition:
a + = + c or 2 + = + 4
Example in multiplication:
5×4×2 = x 2 = 20 x 2 = 40
This property works with multiplication, addition, subtraction, and division.
Distributive Property Of Multiplication Over Addition
Regardless of whether you use the distributive property or follow the order of operations, youll arrive at the same answer. In the first example below, we simply evaluate the expression according to the order of operations, simplifying what was in parentheses first.
Using the distributive law, we:
Lets use a real-life scenario as an example of the distributive property.
Imagine one student and her two friends each have seven strawberries and four clementines. How many pieces of fruit do all three students have in total?
In their lunch bags or, the parentheses they each have 7 strawberries and 4 clementines. To know the total number of pieces of fruit, they need to multiply the whole thing by 3.
When you break it down, youre multiplying 7 strawberries and 4 clementines by 3 students. So, you end up with 21 strawberries and 12 clementines, for a total of 33 pieces of fruit.
Presentation On Theme: Chapter 25 Notes: Reason Using Properties From Algebra Goal: You Will Use Algebraic Properties In Logical Arguments Presentation Transcript:
1 Chapter 2.5 Notes: Reason Using Properties from Algebra Goal: You will use algebraic properties in logical arguments.
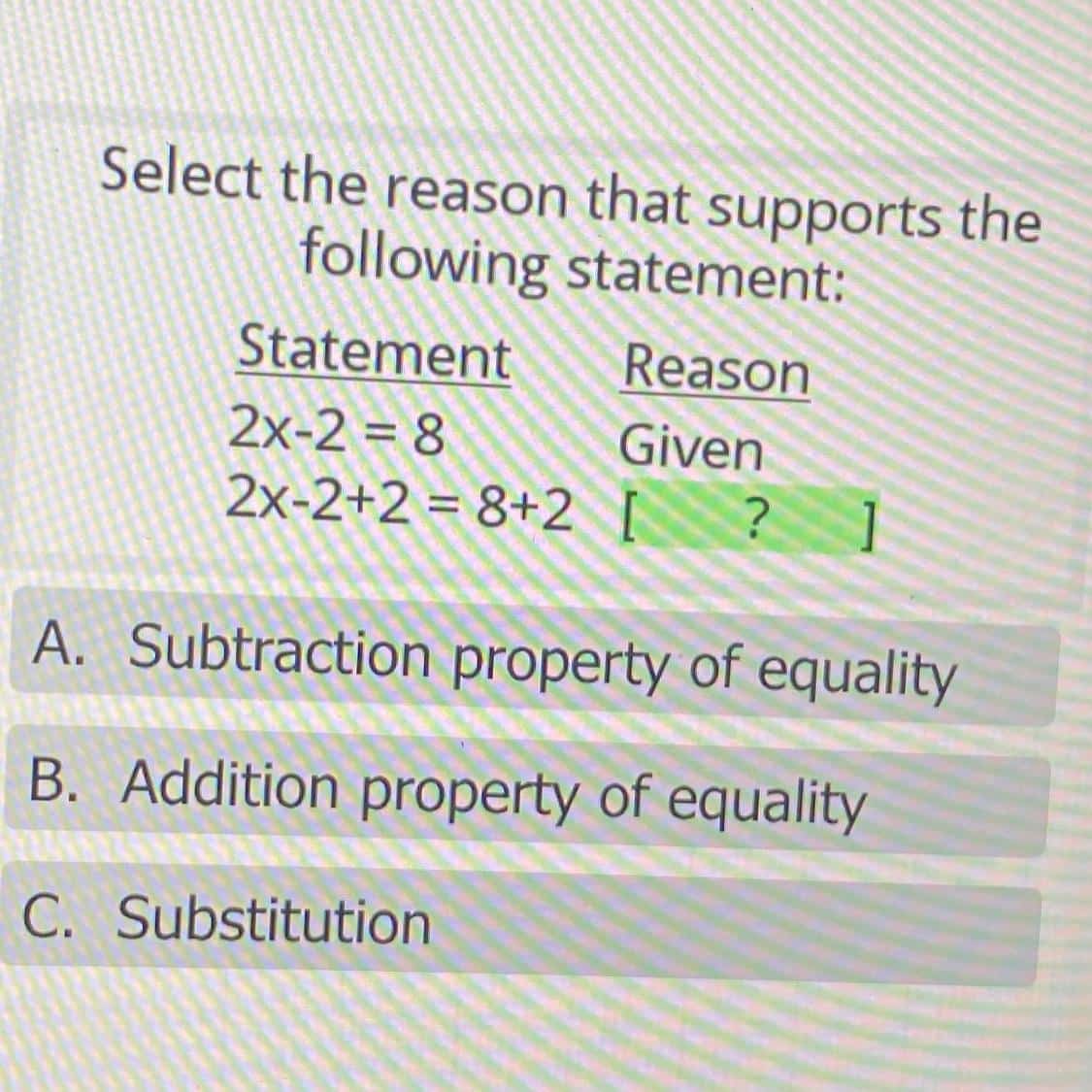
2 Algebraic Properties of Equality: Addition Property: x 5 = 9 Subtraction Property: x + 9 = -21 Multiplication Property:
3 Division Property: 9x = -72 Substitution Property: y = 3x 5 when x = -2 Distributive Property: -3
4 Ex.1: Solve 2x + 5 = 20 3x. Write a reason for each step. Ex.2: Solve -4 = 80. Write a reason for each step. Ex.3: Solve 14x + 3 = -1. Write a reason for each step.
5 Properties: Reflexive Property of Equality: a = ____ i.e. 3 = ____ AB = ____ i.e. GH = ____ _____ i.e. ____ Symmetric Property of Equality: If a = b, then _____________ If AB = CD, then ________________ If, then _______________
6 Transitive Property of Equality If a = b and ____ = c, then ___________ If AB = CD and ____ = EF, then AB = ________ If and ____ =, then ________.
7 Ex.4: You are designing a logo to sell daffodils. Use the information given. Determine whether. Ex.5: In the diagram, AB = CD. Show that AC = BD.
8 Name the property of equality the statement illustrates. Ex.6: If, then. Ex.7: If JK = KL, and KL = 12, then JK = 12. Ex.8:
Don’t Miss: How To Find The Sum In Math
Distributive Property With Exponents
An exponent is a shorthand notation indicating how many times a number is multiplied by itself. When parentheses and exponents are involved, using the distributive property can make simplifying the expression much easier.
Note: For step two, use the FOIL technique to distribute each expression.
Reason Using Properties From Algebra

Solving equations for x Solve 6x+2= -3x-16 for x. Write your reason for each step. 6x+2= -3x-16 +3x +3x 9x+2= -16 -2 -2 9x= -18 X=- 2 Given Addition Property Subtraction Property Division Property
Try in your notebooks Solve 3x+8= -4x-34 for x. Write your reason for each step. 3x+8= -4x-34 +4x +4x 7x+8= -34 -8 -8 7x= -42 x= -6 Given Addition Property Subtraction Property Division Property
How do we write a proof? In the diagram, mABD=mCBE. Show that m1=m3. A mABD=mCBE mABD-m2= m1 mCBE-m2= m3 mABD-m2= mCBE-m2 m1= m3 Given Angle Addition Postulate Angle Addition Postulate Substitution Property Substitution Property 1 C B 2 3 D E What do we know? Whats given to us? What do I need to do to get angle 1? What about angle 3? How are these angles related? How do I know they are equal?
Determine whether to use the symmetric property, reflexive Property or transitive property If m6= m7, then m7=m6. Symmetric Property If JK=KL and KL=MN, then JK=MN. Transitive Property m6=m6. Reflexive Property If mA=m B and m B=m C, then m A=m C. Transitive Property If XY=WZ, then WZ=XY. Symmetric Property AB=AB Reflexive Property
Complete in your notebooks. Page 109 15, 16, 21-25, 28, 31, 33 Extra practice
You May Like: What To Expect In Physics Class
Distributive Property With Variables
Remember what we said about algebraic expressions and variables? The distributive property allows us to simplify equations when dealing with unknown values.
Using the distributive law with variables involved, we can isolate x:
Note: When isolating variables what you do to one side you must do to the other. In order to eliminate 12 on the left side, you must add twelve to both the left and right sides. The same goes for multiplication and division: to isolate x, divide each side by 4.
Algebraic Properties Of Equality
Let a, b and c be real numbers.
Addition Property :
If a = b, then a + c = b + c
Subtraction Property :
If a = b, then a – c = b – c
Multiplication Property :
If a = b, then a c = b c
Division Property :
If a = b and c 0, then a ÷ c = b ÷ c
Reflexive Property :
For any real number a, a = a
Symmetric Property :
If a = b, then b = a
Transitive Property :
If a = b and b = c, then a = c
Substitution Property :
If a = b, then a can be substituted for b in any equation or expression.
Read Also: What Math Courses Are Required For Psychology Major
Distributive Property With Fractions
Solving algebraic expressions with fractions looks more complicated than it is. Follow the steps outlined below to see how its done.
Hopefully, this step-by-step process helps your students understand how and why the distributive property can come in handy when simplifying fractions and complex numbers.
Note: In steps two and three, we find the LCM and use it to multiply the fractions in order to simplify and get rid of them. Need a quick refresher? See our blog post on how to multiply fractions.
What Is The Associative Property
The word “associative” comes from “to associate” or “to group”. The Associative Property is the rule that refers to grouping the regrouping can be of added terms, or of multiplied factors. For addition, the rule is:
a + = + c
In numbers, this means that:
2 + = + 4
For multiplication, the rule is:
a = c
In numbers, this means that:
2 = 4
Any time they refer to the Associative Property, they want you to regroup things any time a computation depends on things being regrouped, they want you to say that the computation uses the Associative Property.
- Rearrange, using the Associative Property: 2
They want me to regroup things, not simplify things. In other words, they do not want me to say “6x“. They want to see me do the following regrouping:
- Simplify 2, and justify your steps.
In this case, they do want me to simplify, but I have to say why it’s okay to do… just exactly what I’ve always done. Here’s how this works:
2 : original statement
x : by the Associative Property
6x : simplification of 2×3
- Why is it true that 2 = x?
Since all they did was regroup things, this is true by the Associative Property.
You May Like: What Is Strain In Physics
Reason Using Properties From Algebra Objective
2. 5 Reason Using Properties from Algebra Objective: To use algebraic properties in logical arguments.
Algebraic Properties Addition Property: If a = b, then a + c = b + c. Subtraction Property: If a = b, then a c = b c. Multiplication Property: If a = b, then ac = bc. Division Property: If a = b and c = 0, then a/c = b/c.
Algebraic Properties Substitution Property: If a = b, then a can be substituted for b in an equation or expression. Distributive Property: a = ab + ac, where a, b, and c are real numbers.
Example 1: Write a two-column proof to solve the equation. 3 x + 2 = 8 Statements Reasons 1. 2. 3. 4. 5. Given 3 x + 2 = 8 3 x + 2 2 = 8 2 3 x = 6 3 x ÷ 3 = 6 ÷ 3 x=2 Subtraction Prop Simplify Division Prop Simplify
Example 2: Write a two-column proof to solve the equation. Statements Reasons 1. 2. 3. 4. 5. 6. Given 4 x + 9 = 16 3 x 4 x + 9 + 3 x = 16 3 x + 3 x 7 x + 9 = 16 7 x + 9 9 = 16 9 7 x = 7 7 x ÷ 7 = 7 ÷ 7 7. x = 1 Addition Prop Simplify Subtraction Prop Simplify Division Prop Simplify
Example 3: Write a two-column proof to solve the equation. 2 = 12 Statements Reasons 1. 2. 3. 4. 5. 6. 2 = 12 -2 x 10 + 10 = 12 + 10 -2 x = 22 -2 x ÷ -2 = 22 ÷ -2 Given Distributive Prop Addition Prop Simplify Division Prop x = -11 Simplify
Example 5 contd: c). m W=m W ANSWER Reflexive Property of Equality d). If L = M and M = 6, then L = 6 ANSWER Transitive Property of Equality
What Is The Commutative Property
Affiliate
The word “commutative” comes from “commute” or “move around”, so the Commutative Property is the one that refers to moving stuff around. For addition, the rule is:
a + b = b + a
In numbers, this means that:
2 + 3 = 3 + 2
For multiplication, the rule is:
ab = ba
In numbers, this means that:
2×3 = 3×2
Any time they refer to the Commutative Property, they want you to move stuff around any time a computation depends on moving stuff around, they want you to say that the computation uses the Commutative Property.
- Use the Commutative Property to restate “3×4×x” in at least two ways.
They want me to move stuff around, not simplify. In other words, my answer should not be “12x” the answer instead can be any two of the following:
4 × 3 ×x
x× 4 × 3
- Why is it true that 3 + = + 3?
Since all they did was move stuff around , this statement is true by the Commutative Property.
Content Continues Below
You May Like: What Is Meant By Geography
Why Do These Properties Seems So Pointless
Why? Because every math system you’ve ever worked with has obeyed these properties! You have never dealt with a system where a×b did not in fact equal b×a, for instance, or where ×c did not equal a×.
You have always been able to move terms around and you have always been able to regroup terms. Which is why the associative and commutative properties probably seem painfully obvious, and hardly worth the time.
Don’t worry about their “relevance” for now just make sure you can keep the properties straight so you can pass the next test. The lesson below explains how I keep track of the properties.
Affiliate
What Is Distributive Property: 5 Effective Examples To Use In Class
What is the distributive property? Also known as the distributive law of multiplication, its one of the most commonly used properties in mathematics.
When you distribute something, you are dividing it into parts. In math, the distributive property helps simplify difficult problems because it breaks down expressions into the sum or difference of two numbers.
According to this principle, multiplying the total of two addends by a number will give us the exact same result as multiplying each addend individually by the number and then adding them together.
Also Check: What Is An Experimental Group In Psychology
Presentation On Theme: 2
1 2-5 Reason Using Properties from AlgebraHubarthGeometry
2 Key ConceptsAlgebraic Properties of EqualityLet a, b, and c be real numbers.Addition PropertyIf a = b, then a + c = b + cSubtraction PropertyIf a = b, then a c = b cMultiplication PropertyIf a = b, then ac = bcDivision PropertyIf a = b, andSubstitution PropertyIf a = b, then a can be substituted for b inany equation or expression
3 Addition Property of EqualityEx 1 Write reasons for Each StepSolve 2x + 5 = 20 3x. Write a reason for each step.EquationExplanationReason2x + 5 = 20 3xWrite original equation.Given2x x =20 3x + 3xAdd 3x to each side.Addition Property of Equality5x + 5 = 20Combine like terms.Simplify.5x = 15Subtract 5 from each side.Subtraction Property of Equalityx = 3Divide each side by 5.Division Property of Equality
4 Distributive PropertyKey ConceptsDistributive Propertya = ab + ac, where a, b, and c are real numbers.Ex 2 Use the Distributive PropertySolve -4 = 80. Write a reason for each step.EquationExplanationReason4 = 80Write original equation.Given44x 8 = 80Multiply.Distributive Property44x = 88Add 8 to each side.Addition Property of Equalityx = 2Divide each side by 44.Division Property of Equality
6 Ex 3 Use Properties of EqualityEquationExplanationReasonMarked in diagram.GivenAdd measures of adjacent angles.Angle Addition PostulateSubstitution Property of EqualityAdd measures of adjacentanglesAngle AdditionPostulateTransitive Property ofEquality