Stock Turnover And Sales
These ratios help businesses measure how quickly they are selling products. They are able to determine where they have excess stock and if they need to change production processes. A stock turnover ratio measures how often a business sells and replaces its goods. Usually, the higher this number is, the higher the ROI. A material to sales ratio measures how a company’s cost of direct materials, like raw materials or wholesale products, compares to its total sales. The higher the material to sales ratio, the higher the ROI and profits will be.
What Is The Golden Ratio
A golden ratio is a distinct number whose value is approximately equal to 1.618. The symbol for this is a Greek letter ‘phi’ represented as Ï. It is a special attribute and is used in art, geometry, and architecture because it is believed that the golden ratio makes the most pleasing and beautiful shape. It is also known as a divine proportion that exists between two quantities and the relationship for calculating the golden ratio is represented as Ï = a/b = /a = 1.61803398875… where a and b are the dimensions of two quantities and a is the larger between the two.
Why Are Ratios Important
Ratios are important because they allow us to express quantities in such a way that they are easier to interpret. It is a tool that is used to compare the size of two or more quantities with respect to each other. For example, if there are 30 girls and 20 boys in a class. We can represent the number of girls to the number of boys with the help of the ratio which is 3: 2 in this case.
You May Like: Why Do Americans Stink At Math
How To Use Ratios In Math
- B.B.A., Finance and Economics, University of Oklahoma
Ratios are a helpful tool for comparing things to each other in mathematics and real life, so it is important to know what they mean and how to use them. These descriptions and examples will not only help you to understand ratios and how they function but will also make calculating them manageable no matter what the application.
How To Calculate Proportion
Sometimes, it is evident without doing any calculations that two ratios are proportional to each other. If you and your dog are the only two animals in a room, and you are told that the adjoining gymnasium contains 457 people and 457 dogs, then you know the proportion of people to dogs is the same in both spaces.
But what about ratios that are not easily compared at a glance? For example, is 17/52 proportional to 3/9? If not, which is greater?One way to do this would be to compute the decimal numbers of each fraction and see which is greater. But if you understand proportions, you can use cross-multiplication instead, multiplying opposite denominators and numerators:
=?= = 153 = 156Thus the ratios are not quite equal , and the fractions are not proportional.
Read Also: What Are Norms In Psychology
Ratios And Proportions And How To Solve Them
Let’s talk about ratios and proportions. When we talk about the speed of a car or an airplane we measure it in miles per hour. This is called a rate and is a type of ratio. A ratio is a way to compare two quantities by using division as in miles per hour where we compare miles and hours.
A ratio can be written in three different ways and all are read as “the ratio of x to y”
$$x\: to\: y$$
$$x:y$$
$$\frac$$
A proportion on the other hand is an equation that says that two ratios are equivalent. For instance if one package of cookie mix results in 20 cookies than that would be the same as to say that two packages will result in 40 cookies.
$$\frac=\frac$$
A proportion is read as “x is to y as z is to w”
$$\frac=\frac \: where\: y,w\neq 0$$
If one number in a proportion is unknown you can find that number by solving the proportion.
Example
You know that to make 20 pancakes you have to use 2 eggs. How many eggs are needed to make 100 pancakes?
| 100 |
$$\frac=\frac\: \: or\: \: \frac=\frac$$
If we write the unknown number in the nominator then we can solve this as any other equation
$$\frac=\frac$$
Multiply both sides with 100
$$ }\, \frac= }\, \frac$$
$$x=\frac$$
$$x=10$$
If the unknown number is in the denominator we can use another method that involves the cross product. The cross product is the product of the numerator of one of the ratios and the denominator of the second ratio. The cross products of a proportion is always equal
$$\frac }} }}=\frac }} }}$$
$$xw=yz$$
Do Ratios Perform A Proportion
In terms of definitions, a ratio is an ordered pair of numbers, such as a and b, often written a:b. So to answer the question of whether ratios perform a proportion, you could say that they do show the proportions of a versus b.
For example, if we are talking about how many smokers there are in an office you could say that the ratio is 1:10. That would mean there is one smoker to every 10 non-smokers â and this ratio is the most simplified way to look at the numbers.
As a proportion, that same concept would be expressed as 1/10. If the office was bigger, you might say that the proportion is 10/100. Each of these two fractions is equivalent to the same proportion.
You May Like: Chapter 9 Test Form 2a Answers Geometry
Example Question #: Gre Quantitative Reasoning
There are 3,500 people in group A and 5,000 people in group B:
|
Car Type |
Quantity A is greater.
Quantity A: To determine the parts of sugar in the dessert, we use the following process. Let’s first figure out the amount of sugar in the cake. This is 4/20. Next, find the amount of sugar in the icing topping: 3/20. Then, we need to account for the amount of cake and icing in the dessert. Using the fact that there are 2 parts cake and 3 parts icing, we can say that 2/5 of the dessert is cake and 3/5 is icing. Combining this information with the amount of sugar in both the cake and the icing, we obtain: 2/5 * 4/20 + 3/5 * 3/20 = 17/100. So, there are 17 parts of sugar in the dessert.
Quantity B: Use the same method to find the amount of milk: 2/5 * 5/20 + 3/5 * 2/20 = 16/100. So there are 16 parts milk in the dessert. Thus, Quantity A is larger.
How To Compare Ratios
There are various methods to compare ratios. For example, let us compare 1: 2 and 2: 3 using the LCM method.
- Step 1: Write the ratios in the form of a fraction. Here, it means 1/2 and 2/3.
- Step 2: Reduce the fractions separately. Here, both the fractions 1/2 and 2/3 are already in their reduced form.
- Step 3: Now, compare 1/2 and 2/3 by finding the LCM of the denominators. The LCM of 2 and 3 is 6.
- Step 4: Make the denominators equal by multiplying the numerator and denominator of the first fraction by 3, that is, / = 3/6. Then, multiply the numerator and denominator of the second fraction by 2, that is, / = 4/6.
- Step 5: Now, 3/6 and 4/6 can be easily compared. This shows that 4/6 is greater than 3/6. Therefore, 2:3 > 1:2.
Read Also: What Does Hemisphere Mean In Geography
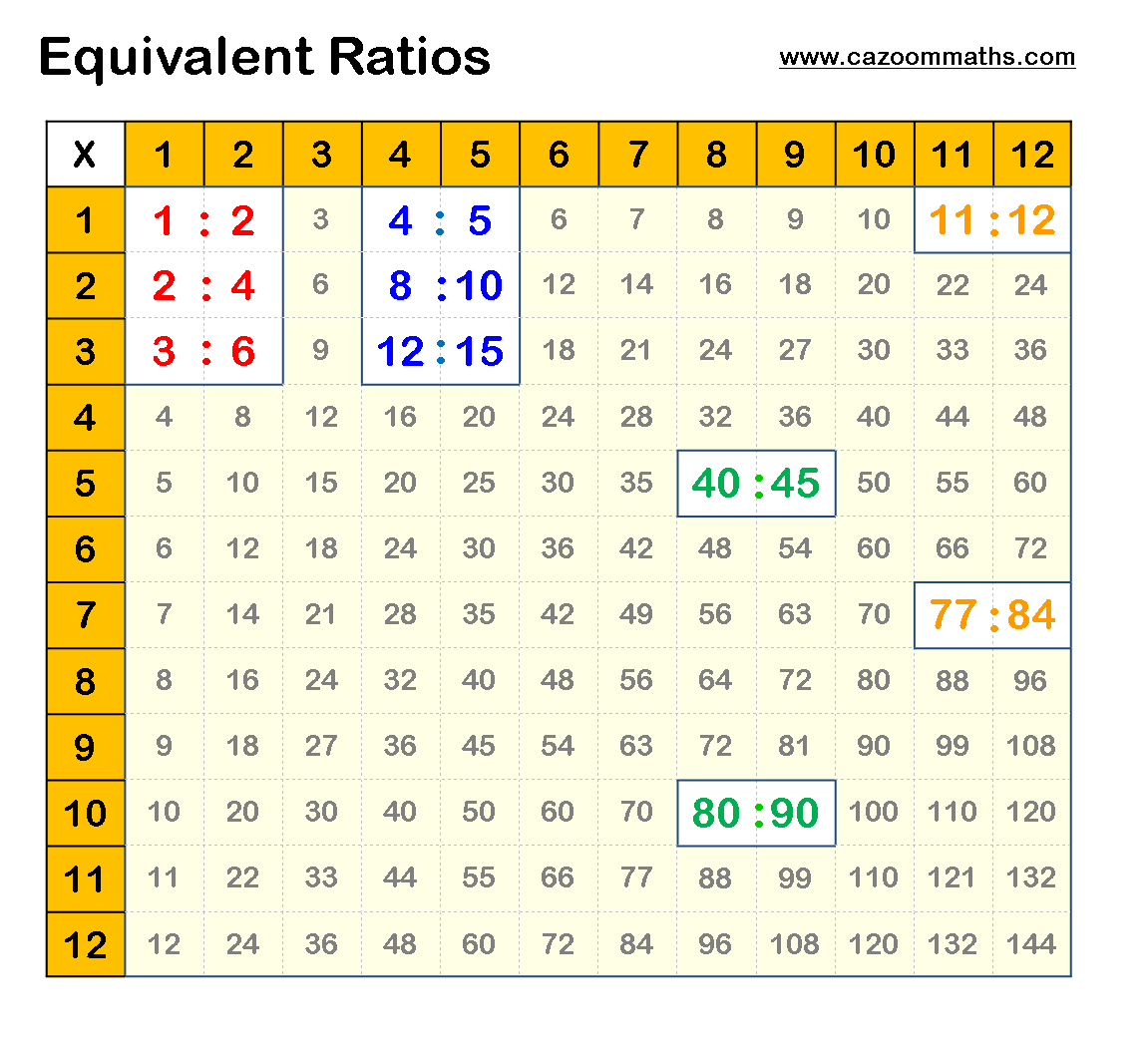
Equivalent Ratios Definition Methods Examples
In this article, you will learn about Equivalent Ratios. In order to understand more, you need to look at the equivalent ratios examples that would help you in getting the right idea on how to find equivalent ratios. Equivalent ratios are ratios that can be simplified or reduced to the same value. In other words, two ratios are equivalent if one can be expressed as a multiple of the other. Some of the equivalent ratios examples are 1:2 and 4:8, 3:5 and 12:20, 9:4 and 18:8, etc.
On this page, we will learn about the definition of Equivalent Ratios, how to find equivalent ratios, some solved example problems on equivalent ratios, and so on.
Also Read:
Practice Calculating Ratios With Greater Than Two Quantities
Use the following demographic information about a marching band to complete the following exercises using ratios comparing two or more quantities.
Gender
1. What is the ratio of boys to girls?
2. What is the ratio of freshmen to the total number of band members?
3. What is the ratio of percussion to woodwinds to brass?
4. What is the ratio of freshmen to seniors to sophomores?
5. If 25 students left the woodwind section to join the percussion section, what would be the ratio for the number of woodwind players to percussion?
Recommended Reading: How Did Geography Impact The Development Of Agricultural Societies
Sample Questions And Their Solutions
Understanding how to work out ratios is an important skill and can be particularly useful when applying for jobs where a good understanding of mathematics is required.
It is a good idea to revise skills like this before taking numerical reasoning or other math-based aptitude tests.
Here are the key ratio skills that you need to master:
Ratio Between A Part And A Whole
In order to find the ratio between a part and a whole, we apply the quotient between a part and a whole. Note that sometimes the total quantities may be given, other times, we would need to calculate it by finding the sum of the parts.
For instance, if m is a part of t, where t is the whole or total of the quantities, the ratio of m to t is,
Meanwhile, the ratio of m to the sum of the quantities m, n and o,
where m + n + o is the total number of quantities.
Out of 6 packs of sweets in a box, Doyle was given 5. What is the ratio of Doyle’s share to the sweets in the box?
Solution
The total packs of sweets in the box is 6, while Doyle’s share of sweets is 5.
Therefore, the ratio of Doyle’s share to the sweets in the box is
A bag contains 3 black balls, 2 red balls and 7 white balls. What is the ratio of white balls to all balls in the bag?
Solution
We first identify what ratio are we calculating. In this case it is white balls ratio to all balls.
Next, we are told that the bag contains 7 white balls.
Next, we find the total number of balls in the bag,
Now having found their values, we express them in ratio,
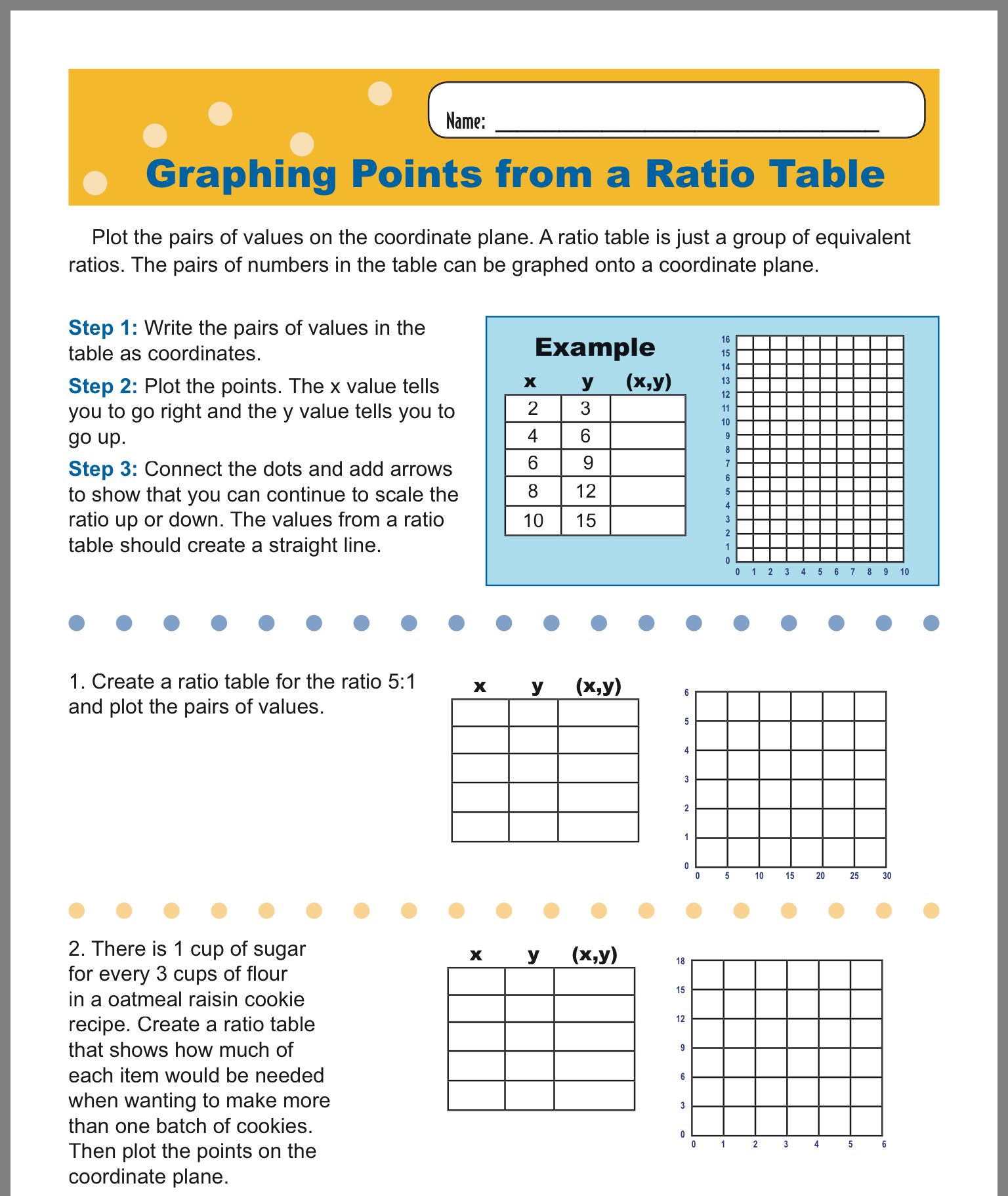
Ratio scale is obtaining equivalent ratios while multiplying or dividing with constants.
While maintaining the same ratio, we can increase or decrease measurements of geometric shapes.
In the illustration below, the length of the rectangle is 4 units while the width is 2 units, thus,
An illustration of ratio scaling – StudySmarter Originals
Don’t Miss: What Does Iso Mean In Biology
Equivalent Ratios Examples With Solutions
Problem 1: Find the value of x and y using the ratio value of 12:20.
Solution:As given in the question the ratio value is 12:20.Now, we need to find the values of x and y.First, let us consider the two ratios that are,12/20 = x/5 = 12×5 = 20x x60 = 20 xx = 60/20 = 30.Hence, the value of x is 30.Next, in order to find the value of y. We have to consider the 1st and 3rd ratios.Here it will be, 12/20 = 9/y12y = 20×9 = 12y = 180y= 180/12 = 15Therefore, the value of y is 15.
Problem 2: What are the two equivalent ratios of 10: 11?
Solution:Given in the question, the ratio value is 10:11.Now, we need to find the two equivalent values.To write the equivalent ratios of a given ratio, we can multiply the terms by any natural number starting from 2.So, we can divide as well if the terms are not co-prime numbers. Here 10 and 11 are co-primes.Let us multiply them by 2 and 3 to find their equivalents.The values are,10:11 = : = 20:2210:11 = : = 30:33Therefore, 20:22 and 30:33 are the two equivalent ratios of 10:11.
Problem 3: The ratios are 15:10 and 30:15. Check whether the given ratios are equivalent or not?
Solution:As given in the question, the ratios are 15:10 and 30:15.Now, we need to find whether the given ratios are equivalent or not.Let us use the cross multiplication method, we can write these ratios are 15/10 and 30.15.Now, we will multiply 15 by 15 and 10 by 30. We get,15 × 15 = 225Here, 225 is not equal to 300.Therefore, the ratios 15:10 and 30:15 are not equivalent ratios.
Convert Ratio To Fraction
A part-to-part ratio states the proportion of the parts in relation to each other. The sum of the parts makes up the whole. The ratio 1 : 2 is read as “1 to 2.” This means of the whole of 3, there is a part worth 1 and another part worth 2.
To convert a part-to-part ratio to fractions:
You May Like: What Is Altruism In Psychology
Examples On Ratio Formula
Example 1: In a class of 70 students, 43 are girls and the remaining are boys. Using the ratio formula, find the ratio of the total number of boys to the number of girls.
Solution:
To find: Ratio of the number of boys to the number of girlsGiven:Total number of students = 70Number of girls = 43Number of boys = Total number of students – Number of girls= 27Using ratio formula,The ratio of number of boys to the number of girls = Number of boys: Number of girls = 27:43
Answer: Ratio of the number of boys to the number of girls = 27:43
Example 2: The ratio of x and y is 6:5. If x = 78, what is the value of y?
Solution:
To find: Value of xGiven: Ratio of x to y = 6:5Using ratio formula,
Answer: Value of y = 65
Example 3: Find the simplest form of 80:75 using the ratio formula.
Solution:
The GCF of 80 and 75 is 5.We divide each term in the ratio by 5.We get 80/5:75/5 = 16:15.
Answer: Thus, the ratio of 80:75 in the simplest form is 16:15.
S How To Solve Ratios
The first step on how to solve the ratio is to write the values you want to compare and you can write such values in any given form like using colon or through division sign or by writing isto. Lets understand the steps through an example. Suppose you want to take out the ratio of your maths and physics marks. You have got 90 marks in maths and 70 marks in physics. So firstly I will write it in the form of a ratio.
90 isto 70 or 90:70 or 90/70.
Second step on how to solve the problem is to reduce the values into their simplest way. So for that you can take out the common factors from the numbers. And then we can divide both of the numbers from such a common factor so that we can get the numbers in their simplest form. For example we have a number 90 : 70 then after writing it in the format of ratios now you have to bring out the common factors between the terms of ratios. So in this example we have 10 as a common factor. Thus you will divide both the numbers 90 and 70 by 10 so that you get the numbers in their simplest form so you will get 90/10:70/10 = 9:7.
Thus the ratio is 9:7.
Lets take another example of three digits and three digits are 75 marks in biology, 25 marks in physics and 100 marks in maths. So lets first write it in the form of ratio that is
75 : 25 : 100
75/25 : 25/25 : 100/25
= 3 : 1 : 4
Thus the answer is 3:1:4.
3 / 4 = 3/X
3 x X = 3 x 2
X = 6/3
Don’t Miss: What Is An Organism In Biology
How Can Comparison Of Ratios Occur
Once the question is given, identify the known ratio according to the facts mentioned. Once both the ratios are ready, use the cross multiplication method and solve the ratios to find out which ratio is greater than the other.
For example – Kenji feeds his cats a mixture of wet and dry food at every meal. He mixes 8 spoonfuls of dry food and 10 spoonfuls of wet food for Tiger, his adult cat. He mixes a smaller meal with 2 spoonfuls of dry food and 7 spoonfuls of wet food for his kitten, Smokey. Do the two meals have the same ratio of dry food to wet food?
Solution – The ratios are 8:10 and 2:7. The LCM of 10 and 7 is 70. Multiplying 8/10 with 7 and 2/7 with 10 to get the common denominators.
/ = 56/70
/ = 20/70
Since one ratio is greater than the other. Therefore, the two meals do not have the same ratio.
What Is The Ratio Formula
The ratio is the relation between the quantities of two or more objects, indicating the amount of one object contained in the other. A ratio can be represented in the form of a fraction using the ratio formula. The ratio formula for any two quantities say a and b is given as,
a:b = a/b
Since a and b are individual amounts for two quantities, the total quantity combined is given as . Let us understand the ratio formula better using a few solved examples.
Don’t Miss: Is Psychology Part Of Stem