+ Addition Plus Positive
The addition symbol + is usually used to indicate that two or more numbers should be added together, for example, 2 + 2.
The + symbol can also be used to indicate a positive number although this is less common, for example, +2. Our page on Positive and Negative Numbers explains that a number without a sign is considered to be positive, so the plus is not usually necessary.
See our page on Addition for more.
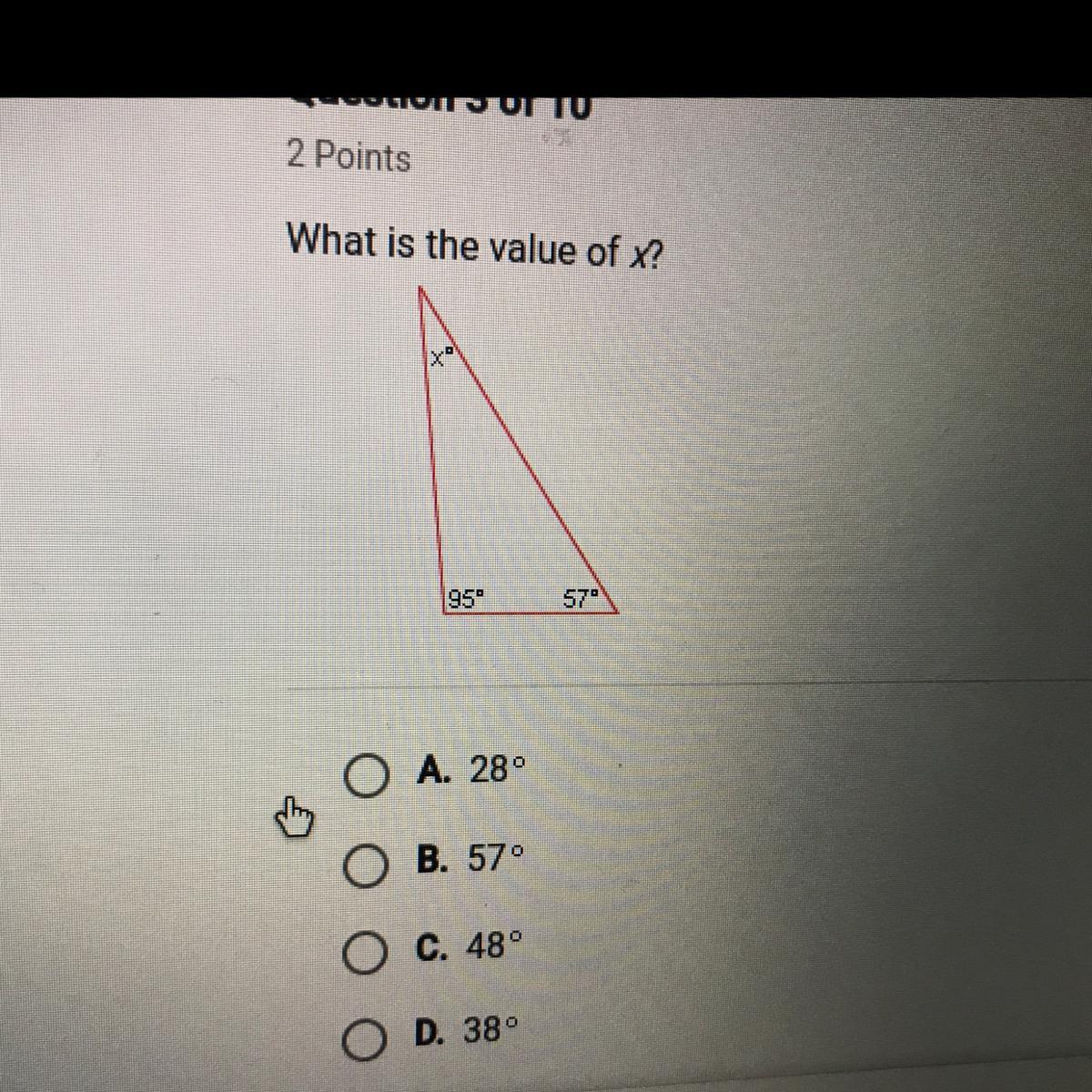
How To Find The Value Of X
In algebra, it is easy to find the third value when two values are given. Generally, the algebraic expression should be any one of the forms such as addition, subtraction, multiplication and division. To find the value of x, bring the variable to the left side and bring all the remaining values to the right side. Simplify the values to find the result.
What Is An Example Of Using The Quadratic Formula
-
Solve x2 + 3x 4 = 0
This quadratic happens to factor, which I can use to confirm what I get from the Quadratic Formula. The Formula should give me the same answers.
x2 + 3x 4 = = 0
…so I already know that the solutions are x = 4 and x = 1.
Now, what would my solution look like in the Quadratic Formula? Using a = 1, b = 3, and c = 4, my solution process looks like this:
So, as expected, the solution is x = 4,x = 1.
For this particular quadratic equation, factoring would probably be the faster method. But the Quadratic Formula is a plug-n-chug method that will always work. Having “brain freeze” on a test and can’t factor worth a darn? Use the plug-n-chug Formula it’ll always take care of you!
Content Continues Below
Also Check: What Is Sensitization In Psychology
< Less Than And > Greater Than
This symbol < means less than, for example 2 < 4 means that 2 is less than 4.
This symbol > means greater than, for example 4 > 2.
These symbols mean less than or equal to and greater than or equal to and are commonly used in algebra. In computer applications < = and > = are used.
These symbols are less common and mean much less than, or much greater than.
What Is E To The Infinity
Eulers Number e is a numerical constant used in mathematical calculations and its value is 2.718281828459045so on. It implies that e increases at a very high rate when e is raised to the infinity of power and thus leads towards a very large number so we conclude that e raised to the infinity of power is infinity.
Read Also: Pearson Texas Algebra 1 Form K
How Do You Solve For X
To solve for x, bring the variable to one side, and bring all the remaining values to the other side by applying arithmetic operations on both sides of the equation. Simplify the values to find the result.Lets start with a simple equation as, x + 2 = 7How do you get x by itself?Subtract 2 from both sides x + 2 – 2 = 7 – 2 x = 5Now, check the answer, x = 5 by substituting it back into the equation. We get 5 + 2= 7.L.H.S = R.H.S
What Is A Solution Of An Equation
The value of the variable which makes the equation a true statement is the solution of the equation.
Example 1:
Verify that x = 3 is the solution of an equation 4x 8 = 5 + 3x
Substitute x = 3 in the given equation
4x 8 = 4 8 = 12 8 = 4
5 + 3x = 5 + 3 = 5 + 9 = 4
LHS = RHS
So, x = 3 is the solution of an equation 4x 8 = 5 + 3x.
Example 2:
Verify that y = 2 is the solution of an equation 2m 4 = 1
Substitute y = 2 in the given equation.
2m 4 = 2 4 = 4 4 = 8
So, y = 2 is not the solution of given equation 2m 4 = 1.
Don’t Miss: Stuff You Must Know Cold Geometry Answers
I Looked Up The Definition Of Multiplication
To be able to apply the commutative property, we must first establish a definition of multiplication that applies meaning to the operand order. If operand order isnt important, the commutative property serves no useful distinction.
In Wikipedias definition of multiplication, they indicate the first factor is the number of copies and the second is the number being repeated.
If this is the definition the teacher taught, 5 x 3 is equivalent to 5 copies of 3, or 3 + 3 + 3 + 3 + 3. It is equal but not equivalent to 5 + 5 + 5 because 3 copies of 5 represents something different.
For example, 3 bundles of 5 bananas is different from 5 bundles of 3 bananas although they total to the same number of bananas. Their structures are different.
Heres another example: 30 ÷ 2 is equal to 15. But does 30 ÷ 2 represent multiplication? Is it equivalent to repeated addition?
No, it represents division. It is equal to 5 times 3 but not equivalent.
Determine Whether A Decimal Is A Solution Of An Equation
Solving equations with decimals is important in our everyday lives because money is usually written with decimals. When applications involve money, such as shopping for yourself, making your familys budget, or planning for the future of your business, youll be solving equations with decimals.
Now that weve worked with decimals, we are ready to find solutions to equations involving decimals. The steps we take to determine whether a number is a solution to an equation are the same whether the solution is a whole number, an integer, a fraction, or a decimal. Well list these steps here again for easy reference.
HOW TO: DETERMINE WHETHER A NUMBER IS A Solution TO AN EQUATION
- Step 1. Substitute the number for the variable in the equation.
- Step 2. Simplify the expressions on both sides of the equation.
- Step 3. Determine whether the resulting equation is true.
- If so, the number is a solution.
- If not, the number is not a solution.
Example \:
Determine whether each of the following is a solution of x 0.7 = 1.5: x = 1 x = 0.8 x = 2.2
Solution
Recommended Reading: What Are The Three Types Of Research Methods In Psychology
Solve Equations With Decimals
- Determine whether a decimal is a solution of an equation
- Solve equations with decimals
- Translate to an equation and solve
be prepared!
Before you get started, take this readiness quiz.
How Does The Quadratic Formula Relate To X
The solutions to the quadratic equation, as provided by the Quadratic Formula, are the x-intercepts of the corresponding graphed parabola.
How? Well, when y = 0, you’re on the x-axis. The x-intercepts of the graph are where the parabola crosses the x-axis. You’re applying the Quadratic Formula to the equation ax2 + bx + c = y, where y is set equal to zero.
Looking at the above example, there were two solutions for the equation x2 + 3x 4 = 0. This tells us that there must then be two x-intercepts on the graph. Graphing, we get the curve below:
Affiliate
As you can see, the x-intercepts match the solutions, crossing the x-axis atx = 4 and x = 1. This shows the connection between graphing and solving: When you are solving ” = 0″, you are finding the x-intercepts of the graph. This can be useful if you have a graphing calculator, because you can use the Quadratic Formula to solve a quadratic, and then use your graphing calculator to make sure that the displayed x-intercepts have the same decimal values as do the solutions provided by the Quadratic Formula.
Note, however, that the calculator’s display of the graph will probably have some pixel-related round-off error, so you’d be checking to see that the computed and graphed values were reasonably close don’t expect an exact match.
-
Solve 2x2 4x 3 = 0. Round your answer to two decimal places, if necessary.
Then the answer is x = 0.58, x = 2.58, rounded to two decimal places.
Recommended Reading: What Ph Stands For In Chemistry
What Does It Look Like
The absolute value of 5 is 5, it is the distance from 0, 5 units.
The absolute value of -5 is 5 it is the distance from 0, 5 units.
$$|x| = 2 $$
$$For \space |x| < 2, -2 < x < 2$$ $$For \space |x| = 4, -4 = x = 4$$
|7| = 7 means the absolute value of 7 is 7.
|-7| = 7 means the absolute value of -7 is 7.
|-2 – x| means the absolute value of -2 minus x.
-|x| means the negative of the absolute value of x.
Solving Equations In One Variable
![What does X equal in [math]\sqrt{x+15} + \sqrt{x} = 15 [/math]?](https://www.tutordale.com/wp-content/uploads/what-does-x-equal-in-mathsqrtx15-sqrtx-15-math-quora.png)
An equation is a mathematical statement formed by placing an equal sign between two numerical or variable expressions, as in 3 11 .
A solution to an equation is a number that can be plugged in for the to make a true number statement.
Example 1:
is the ONLY solution to 3 11 .
Some equations might have more than one solution, infinitely many solutions, or no solutions at all.
Example 2:
is true for all real numbers . It has infinitely many solutions.
Example 4:
is never true for any real number. It has no solutions .
The containing all the solutions of an equation is called the for that equation.
| Equation | |
| x |
Sometimes, you might be asked to solve an equation over a particular . Here the possibilities for the values of x
This is a slightly tricky equation it’s not and it’s not , so we don’t have a good method to solve it. However, since the domain only contains four numbers, we can just use trial and error.
So the over the given domain is { .
Recommended Reading: More Work With The Quadratic Formula Common Core Algebra 2
Investigating The Nature Of Roots
Use the quadratic formula to determine the roots of the quadratic equations given below and take special note of:
| rational | |
| irrational | undefined |
What Does The Notation Mean In This Question
Taken from the Rhode Island Mathletes Documentation from 1986
if $$ is the largest integer not bigger than $x$, what is $ + $
I’m not sure what this question is asking at all, for a start, how can $$ be less than $x$? And what do the brackets mean at all?
- 1$\begingroup$The definition is given to you: “$$ is the largest integer not bigger than $x$.” You may know this as “the result after rounding down $x$ to the nearest integer.” We do have $=x$ if $x$ is an integer, but in general it might be that $ < x$.$\endgroup$ angryavianOct 26, 2017 at 2:28
- $\begingroup$The meaning of the brackets is explained in the line you quoted: $[x[$ means the largest integer not bigger than $x.$$\endgroup$Oct 26, 2017 at 2:28
- $\begingroup$This is a common notation. See en.wikipedia.org/wiki/Floor_and_ceiling_functions#Notation$\endgroup$Oct 26, 2017 at 2:29
- $\begingroup$@bof So basically means to floor the value of $x$?$\endgroup$ TravisOct 26, 2017 at 2:31
- $\begingroup$”How can $$ be less than $x$?” If $x$ is not an integer, then $$ has to be less than $x.$ It can’t be equal to $x$ because it’s an integer and $x$ is not an integer it can’t be bigger than $x$ because it’s “not bigger than $x $ the only possibility left is that it’s less than $x.$ For example, if $x=3.5$ then $=3\lt3.5=x.$$\endgroup$
Recommended Reading: Geometry Dash The Secret Box
Check Both Answers By Substituting Back Into The Original Equation
For \: \begin 6x^2-4x + 6 & = 0 \\ 6x^2-12x + 6 & = 0 \\ x^2-2x + 1 & = 0 \\ & = 0 \\ ^2& = 0 \\ \text x & = 1 \end
We see that for \ the quadratic equation has real, equal roots \.
For \: \begin 6x^2-4x + 6 & = 0 \\ 6x^2+12x + 6 & = 0 \\ x^2+2x + 1 & = 0 \\ & = 0 \\ ^2& = 0 \\ \text x & = -1 \end
We see that for \ the quadratic equation has real, equal roots \.
How To Solve Linear Equations With One Variable
- Simplify the expressions inside parentheses, brackets, braces and fractions bars.
- The same quantity can be added, subtracted, multiplied or divided from both sides of an equation without changing the equality.
Any term of an equation may be taken from one side to the other with the change in its sign. This process is called transposition.
Example:
4a + 7a = 13 + 9
11a = 22
a = $\frac$
a = 2
$\frac + 3w = $\frac$
3w = $\frac \frac$
3w = $\frac$
w = $\frac$
w = $\frac$
Example 1: Solve for x.
x + 8 = 12
Solution:
Here is the equation to solve: x + 8 = 12
We need to leave x alone on one side of the equation. For this, we must take 8 out of both sides.
So, x + 8 8 = 12 8
or, x = 4
Example 2:Determine if the value 3 is a solution of the equation:
4x 2 = 3x + 1
Solution:
We will substitute the value of 3 in this equation and will check if the left-side equation is equal to the right-hand side.
or, 12 2 = 9 + 1
or, 10 = 10
Yes, 3 is a solution to the given equation.
Example 3: Solve the equation: 6 + x 7 = 3 + 2x
Solution:
6 + x 7 = 3 + 2x
Expanding the terms we get,
12x + 18 + x 7 = 15x + 21 + 2x
or, 13x + 11 = 17x + 21
On further simplification,
Read Also: How To Calculate Hybridisation In Chemistry
What Does X Equal To In Math
The letter x is often used in algebra to mean a value that is not yet known. It is called a variable or sometimes an unknown. In x + 2 = 7, x is a variable, but we can work out its value if we try! A variable doesnt have to be x, it could be y, w or any letter, name or symbol.
Is X 1 divided by X?
No it does not: When you divide something by x it is undefined for x=0. So when you simplify correctly you will also have the answer to your question.
Whats the difference between a size 1x and 1x?
At one end of the scale a size 1x was equal to 14/16 and at the other end of the scale a size 1x was equal to 22/24. Lets take a look at three examples below. For our short case study we will use a size 1x for comparison. Example 1: Avenue
Linear Equations With One Variable
The simplest examples of equivalent equations don’t have any variables. For example, these three equations are equivalent to each other:
Recognizing these equations are equivalent is great, but not particularly useful. Usually, an equivalent equation problem asks you to solve for a variable to see if it is the same as the one in another equation.
For example, the following equations are equivalent:
In both cases, x = 5. How do we know this? How do you solve this for the “-2x = -10” equation? The first step is to know the rules of equivalent equations:
- Adding or subtracting the same number or expression to both sides of an equation produces an equivalent equation.
- Multiplying or dividing both sides of an equation by the same non-zero number produces an equivalent equation.
- Raising both sides of the equation to the same odd power or taking the same odd root will produce an equivalent equation.
- If both sides of an equation are non-negative, raising both sides of an equation to the same even power or taking the same even root will give an equivalent equation.
Also Check: What Is Integrated Math 3 Equivalent To
How To Solve Squares
You can re-write a square equation into numbers that are easier to deal with using this formula
n^2 = + d^2
where n is the number to be squared, and d is the difference
Heres an example
57^2 = + 3^2# we add 3 to 57, as 60 is easier to multiply than 57, and subtract 3 from the second 57-> 60 x 54 + 9 = 3000 + 240 + 9 = 3249
The ultimate example is when you are squaring a number ending in 5, then round one number up to the nearest 10, the other number down to the nearest 10, and add 25.
65^2 = + 5^2 = 4200 + 25 = 4225
How Do I Use The Quadratic Formula

To use the Quadratic Formula, you must:
-
Arrange your equation into the form ” = 0″.
-
Arrange the terms in the in decreasing order .
-
Pull out the numerical parts of each of these terms, which are the “a“, “b“, and “c” of the Formula.
-
Plug these numbers into the formula.
-
Simplify to get your answers.
Advisories: The “2a” in the denominator of the Formula is underneath everything above, not just the square root. And it’s a “2a” under there, not just a plain “2”. Make sure that you are careful not to drop the square root or the “plus/minus” in the middle of your calculations, or I can guarantee that you will forget to “put them back in” on your test, and you’ll mess yourself up. Remember that “b2″ means “the square of ALL of b, including its sign”, so don’t leave b2 being negative, even if b is negative, because the square of a negative is a positive.
In other words, don’t be sloppy and don’t try to take shortcuts, because it will only hurt you in the long run. Trust me on this!
Recommended Reading: What Is Sum In Math