From Guesses To Proofs
It is important to note that this method produces only a guess fora formulait doesnt actually prove that the formula iscorrect in general. For example, in the squares problem it is conceivable thatthe formula works only for values of n up to 6, and thenfails after that or maybe it works for all values of n up to amillion, but doesnt work for n = 1,000,001. We cantest more values of n, drawing more and more squares, countingthe number of vertices, and comparing this with the value predicted by theformula, but we wont ever be able to test every possible valueof n. So how can we be positive that the formula will alwayswork?
Finding a proof for a conjecture can be difficult and may require a verycreative way of looking at the problem. There are some conjectures in math thathave eluded all attempts at proof for hundreds of years. On the other hand,many conjectures can be proved with just a bit of thought. A mathematical proofdoes not have to follow a strict format or be encrusted with strange-lookingsymbols all that is required is an explanation following a careful, logicaltrain of thought that shows why the conjecture must be true.
Lets try to prove our conjecture that the total number of vertices inthe squares problem is given by the formulaf = 3n + 1. We mightfirst ask ourselves, Why does the formula end with+1? What significance does that have? What does itcorrespond to?
f = 31,000,000 + 1= 3,000,001.
How Do I Approach Finding Limit Of A Two Recursive Sequences
Problem: Given Some alpha, betta > 0, x_0, y_0 and
x_=/ y_=/
Analyze them on divergence and find a limit if it exists.
Where do I start?
Hi ,
Please read the following message. You are required to explain your post and show your efforts.
If you haven’t already done so, please add a comment below explaining your attempt to solve this and what you need help with specifically. See the sidebar for advice on ‘how to ask a good question’. Don’t just say you “need help” with your problem.
This is a reminder for all users. Failure to follow the rules will result in the post being removed. Thank you for understanding.
I am a bot, and this action was performed automatically. Please if you have any questions or concerns.
I don’t know the usual way of doing this, but you can
Write the recursive formulas as a 2D matrix equation, where _ = M · _n
Diagonalize M, then determine the limit of _n = Mn · _0
that’s awesome! but for now, I’m a freshman, and on linear algebra we still didn’t learn words “diagonalize”.
it would be awesome if there existed a way to do it only with calculus ideas
Added an image to the post for better readability
I think the first thing to notice is that these sequences are taking successive weighted averages. Because of this, all the xn and yn will be between x0 and y0. In this kind of situation, it’s often useful to consider the difference, xn – yn.
What Is A Sequence Number
Logic numerical problems generally consist of one or two missing numbers and 4 or more visible terms.
For this case, a test designer produces a sequence in which the only one fits the number. By learning and excising number sequence, an individual can sharpen their numerical reasoning capability, which helps our daily activities such as calculating taxes, loans, or doing business. For this case, it is important to learn and practice number sequence.
Example 1
Which list of numbers makes a sequence?
Solution
The first list of numbers does not make a sequence because the numbers lack proper order or pattern.
The other list is a sequence because there is a proper order of obtaining the preceding number. The consecutive number is obtained by adding 3 to the preceding integer.
Example 2
Find the missing terms in the following sequence:
8, _, 16, _, 24, 28, 32
Solution
Three consecutive numbers, 24, 28, and 32, are examined to find this sequence pattern, and the rule obtained. You can notice that the corresponding number is obtained by adding 4 to the preceding number.
The missing terms are therefore: 8 + 4 = 12 and 16 + 4 = 20
Example 3
What is the value of n in the following number sequence?
12, 20, n, 36, 44,
Solution
Identify the pattern of the sequence by finding the difference between two consecutive terms.
44 36 = 8 and 20 12 = 8.
The pattern of the sequence is, therefore, the addition of 8 to the preceding term.
Also Check: What Is Gene Expression In Biology
Defining A Sequence By Recursion
Sequences whose elements are related to the previous elements in a straightforward way are often defined using recursion. This is in contrast to the definition of sequences of elements as functions of their positions.
To define a sequence by recursion, one needs a rule, called recurrence relation to construct each element in terms of the ones before it. In addition, enough initial elements must be provided so that all subsequent elements of the sequence can be computed by successive applications of the recurrence relation.
The Fibonacci sequence is a simple classical example, defined by the recurrence relation
- a
,\dots ,c_} are polynomials in n. For most holonomic sequences, there is no explicit formula for expressing a n } as a function of n. Nevertheless, holonomic sequences play an important role in various areas of mathematics. For example, many special functions have a Taylor series whose sequence of coefficients is holonomic. The use of the recurrence relation allows a fast computation of values of such special functions.
Not all sequences can be specified by a recurrence relation. An example is the sequence of prime numbers in their natural order .
What Are The 5 Stages Of Learning Numeracy
The stages of learning early numeracy concepts are: emergent, perceptual, figurative, counting on and facile. An overview of expected understandings in each stage is included below, and examples of assessment tasks for some stages are available as well.
What is number series with example?
The above series involves two operations: multiplication and addition of a number by the same number. The series runs like this: 1 x 2 + 2 = 3, 3 x 3 + 3 = 12, 12 x 4 + 4 = 52, 52 x 5 + 5 = 265. The next number, following this logic should be 265 x 6 + 6 = 1596.
How do you solve no series questions?
What are number series explain with example?
A sequence of numbers which follow a particular pattern is called number series. In number series questions, some specific pre-decided rules are hidden and the candidate needs to find at that hidden rule to arrive at correct answer. For example, consider 1, 4, 7, 10, 13..
What are the 5 types of sequence?
There are many famous sequences. Some of the most common are arithmetic sequences, geometric sequences, the Fibonacci sequence, the triangular number sequence, the square numbers sequence, and the cube numbers sequence.
How do you do sequences in math?
Introduction To Sequences | Algebra | Maths | FuseSchool YouTube
How do you get an A+ in math?
How To Get A+ In Math Exam
Read Also: Holt Mcdougal Algebra 1 Practice Workbook Answer Key
What Is The Next Number In The Sequence 1 2 4 7
Here are three solutions :
Solution 1: Add 1, then add 2, 3, 4, …
So, 1+1=2, 2+2=4, 4+3=7, 7+4=11, etc…
Rule: xn = n/2 + 1
| 5 | 5 |
The last row shows that we are always wrong by 5, so just add 5 and we are done:
Rule: xn = 2n + 5
OK, we could have worked out “2n+5” by just playing around with the numbers a bit, but we want a systematic way to do it, for when the sequences get more complicated.
What Is The Formula Of Sequence
The general term nth term defines a sequence. If a sequence belongs to specific types like arithmetic, geometric, etc, then we have formulas to find the general term of the respective sequence. Otherwise, one has to observe the numbers of the sequence to identify the pattern. For example, the sequence 1, 27, 125, …, does not represent any type of sequence but one can notice that it represents the cubes of odd natural numbers.
Recommended Reading: How Does Math Impact Our Lives
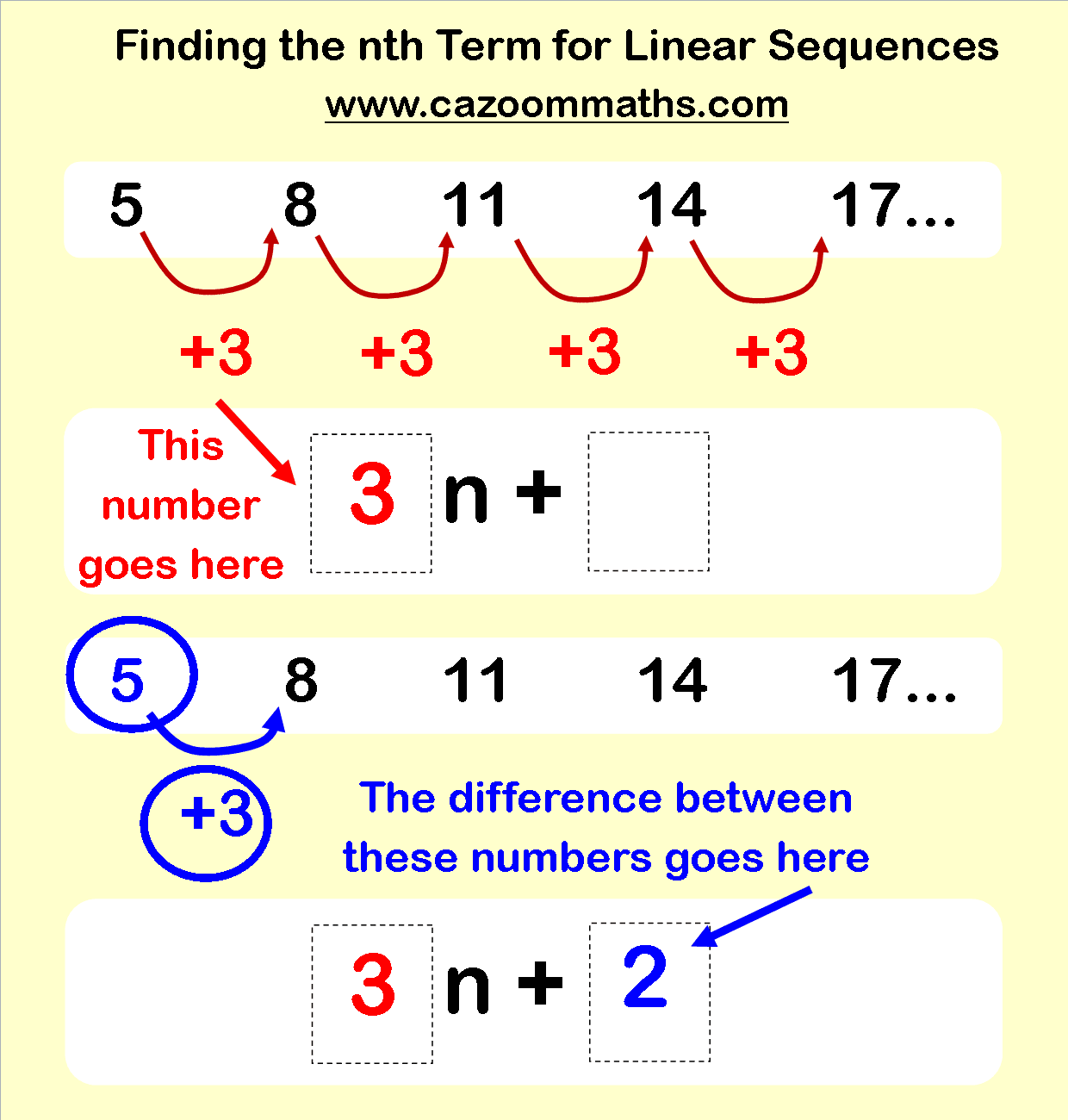
How To Find The Nth Term Of A Sequence
To find the nth term of a sequence, follow these steps:
The nth term is a formula that is used to create a sequence. Simply substitute values in place of n to find the relevent term. To find the first term, substitute n = 1. To find the second term, substitute n = 2.
Here is the 2n sequence.
The 2n sequence begins with 2, 4, 6, 8 and so on.
The 2n sequence is the two times table. The difference between each number is 2.
Here is an example of finding the nth term of the sequence 2n + 3.
The sequence is 5, 7, 9, 11.
The first step is to find the common difference between each term. This term is going up in twos.
The second step is to write this difference multiplied by n. We have 2n.
The third step is to decide what number should be added to this difference to make the first term.
The difference is 2 and the first term is 5. We need to add 3 to 2 to make 5.
The final step is to write this on the end of the expression. 2n becomes 2n + 3.
We can see that the 2n + 3 sequence goes up in twos like the 2n sequence, however all numbers are 3 larger.
Here is another example of finding the nth term of a sequence.
We have 3, 8 13, 18.
The difference between each term is 5. So we start with the 5n sequence.
We need to subtract 2 from 5 to make the first term of 3 and so the sequence is 5n 2.
How To Find A Missing Term In An Arithmetic Sequence
To find a missing term in an arithmetic sequence, first identify the common difference by subtracting any term from the term that comes immediately after it. Count up or down by this amount from term to term until you find the missing value needed.
An arithmetic sequence is simply a list of numbers that are formed by adding on the same amount each time to get from one number to the next.
Here is the sequence 3, _, 7, 9, 11. The second term is missing.
To find the common difference, we subtract any term from the term that comes after it.
11 9 = 2 and 9 7 = 2. We can see that the common difference is 2.
We can add 2 to 3 to find the missing term of 5.
Alternatively, we can subtract 2 from 7 to find the missing term of 5.
Here is an example of finding 2 missing terms in a sequence.
We have the sequence _, 10, _, 24, 31.
We first need to find the common difference between two terms. We need to look at two consecutive terms, which are two numbers in the sequence that are next to each other.
31 24 = 7 and so, the common difference of this sequence is 7.
We can count down in sevens to find the missing terms.
24 7 = 17 and 10 7 = 3. 17 and 3 are the missing terms in the sequence.
Recommended Reading: What Kind Of Jobs Can You Get With Psychology Degree
Finding Missing Numbers In A Number Sequence
- A number sequence is a list of numbers that follow a pattern.
- An example of a number sequence is 5, 9, 13, 17.
- To find the difference between each number, subtract one number from the number that comes after it.
- 9 5 = 4 and so, the common difference is 4.
- Each number in a sequence is called a term.
- To find the next term in the sequence, add 4 to 17 to make 21.
A sequence can be formed by adding the same number each time.
Subtract one number from the number that comes after it to find this common difference.
- To find the difference between each number, we subtract one term from the term that is immediately after it.
- 32 22 = 10 and so, this sequence is going up by 10 each time.
- We can add 10 to 32 to find the missing number of 42.
- Alternatively, we can subtract 10 from 52 to find 42.
How to Find the Next Number in a Number Sequence
How to Find a Missing Number in a Linear Number Sequence
How to Find the Common Difference in a Number Sequence
Finding the Next Number in a Sequence Worksheets and Answers
What Do We Really Know About Teaching Kids Math
- Save this story for later.
- Save this story for later.
Earlier this week, I wrote about the history of progressive math education, the culture wars it has inspired over the past hundred years, and the controversy over the California Math Framework. Today, I want to start with a much broader question: What do we really know about how to teach math to children?
The answer is not all that muchand what little we do know is highly contested. An American math education usually proceeds in a linear fashion, with the idea that one subject prepares you for the next. Take, for example, the typical path through mathematics for a relatively advanced student. They will start with basic arithmetic, learn multiplication and division, and graduate to fractions. Then theyll go into algebra, then geometry, then Algebra II/trigonometry, before tackling calculus. There may be small variations to this sequence, but thats more or less how most kids learn math in the U.S.
Read Part I of Jay Caspian Kangs series on math education.
Even though the wars rage, partly because there are some true believers on both sides and partly because some stand to profit from the conflict, I remain convinced that there is a large middle ground. I believe that the vocal extremes, partly by screaming for attention and partly by claiming the middle ground , have exerted far more influence than their numbers should dictate.
Don’t Miss: How To Calculate Half Life Chemistry
Number Sequence Problems: Value Of A Particular Term
A number sequence problem may first describe how a sequence of numbers is generated. After acertain number of terms, the sequence will repeat. Follow the description of the sequence andwrite down numbers in sequence until you can determine how many terms occur before the numbersrepeat. Then use that information to determine what a particular term could be.
For example:If we have a sequence of numbers:x, y, z, x, y, z, .that repeats after the third term, to find the fifth term we find the remainder of 5 dividedby 3, which is 2. .
The fifth term is then the same as the second term, which is y.
Example:The first term in a sequence of numbers is 2. Each even-numbered term is 3 more than theprevious term and each odd-numbered term, excluding the first, is 1 times the previousterm. What is the 45th term of the sequence?
Solution:Step 1: Write down the terms until you notice a repetition.2, 5, -5, – 2, 2, 5, -5, -2,
The sequence repeats after the fourth term.Step 2: To find the 45th term, find the remainder for 45divided by 4, which is 1.
Step 3: The 45th term is the same as the 1st term, whichis 2.
Answer: The 45th term is 2.
What Are Finite And Infinite Sequences And Series

Sequences: A finite sequence is a sequence that contains the last term such as a1, a2, a3, a4, a5, a6an. On the other hand, an infinite sequence is never-ending i.e. a1, a2, a3, a4, a5, a6an..
Series: In a finite series, a finite number of terms are written like a1 + a2 + a3 + a4 + a5 + a6 + an. In case of an infinite series, the number of elements are not finite i.e. a1 + a2 + a3 + a4 + a5 + a6 + an +..
Read Also: What Is Co In Chemistry
Arithmetic Sequences And Series
An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant.
Example
2,4,6,8,10.is an arithmetic sequence with the common difference 2.
If the first term of an arithmetic sequence is a1 and the common difference is d, then the nth term of the sequence is given by:
$$a_=a_+d$$
An arithmetic series is the sum of an arithmetic sequence. We find the sum by adding the first, a1 and last term, an, divide by 2 in order to get the mean of the two values and then multiply by the number of values, n:
$$S_=\frac$$
Example
Find the sum of the following arithmetic series 1,2,3..99,100
We have a total of 100 values, hence n=100. Our first value is 1 and our last is 100. We plug these values into our formula and get:
$$S_=\frac=5050$$
What Is The Easiest Way To Learn Number Series
Number Series tricks for bank po YouTube
How can I improve my wrong number series?
If you know the basics of the number series, then it will be easier for you.
| Pattern 1 | Pattern 2 |
|---|---|
| 12×1 = 12 12x = 18 18x = 45 45x = 180 180x= 1170 1170x = 12285 | 12x = 12 12x = 18 18x = 45 45x = 180 180x = 1080 1080x = 9180 |
What are the 4 types of sequences?
There are four main types of different sequences you need to know, they are arithmetic sequences, geometric sequences, quadratic sequences and special sequences.
What are the 4 types of sequence in math?
How do sequences work in math?
Sequences are ordered lists of numbers , like 2,5,8. Some sequences follow a specific pattern that can be used to extend them indefinitely. For example, 2,5,8 follows the pattern add 3, and now we can continue the sequence. Sequences can have formulas that tell us how to find any term in the sequence.
How can I improve my numerical skills?
Strategies
| nth term from the last term | an = l d |
What kind of sequence is 1234?
This is an arithmetic sequence since there is a common difference between each term. In this case, adding 1 to the previous term in the sequence gives the next term. In other words, an=a1+d a n = a 1 + d . This is the formula of an arithmetic sequence.
What is sequence formula?
Also Check: How To Cite Campbell Biology 9th Edition