What Is Mgh In Physics

Work Done Against Gravity

Climbing stairs and lifting objects is work in both the scientific and everyday senseâit is work done against the gravitational force. When there is work, there is a transformation of energy. The work done against the gravitational force goes into an important form of stored energy that we will explore in this section.

What Is Pe Mgh

P.E.mgh

Similarly, you may ask, what does PE MGH stand for?

Potential energy = mass x gravity x height

Subsequently, question is, what is Ke and PE? Kinetic Energy Potential Energy KE is the energy possessed by an object by virtue of it being in motion. PE is the energy possessed by an object by virtue of its position. It can be transferred from one object to another and this happens during collisions.

Also to know is, what is the ball’s potential energy PE?

That’s how much potential energy is stored in the ball. Potential Energy concentrated in the ball equals Force of Gravity times the distance the ball will fall, or PE = Fg x H. If you remember Newton’s laws of motion, you will remember that Force equals mass times acceleration.

What is an example of GPE?

Gravitational energy is the potential energy held by an object because of its high position compared to a lower position. For example, a pen being held above a table has a higher gravitational potential than a pen sitting on the table. Gravitational potential energy is mechanical energy minus kinetic energy.

Can Force Be Negative

To answer the question can force be negative, we need to understand the concept of positive direction and negative direction.

• Force is negative If the applied force is in opposite direction to the displacement of the moving object.
• Forces that are aimed at the right are usually called positive forces.
• Forces that are aimed to the left are usually said to be in a negative direction.

Recommended Reading: Abiotic Ecology Definition

Potential Energy For Near Earth Gravity

For small height changes, gravitational potential energy can be computed using

where m is the mass in kg, g is the local gravitational field , h is the height above a reference level in metres, and U is the energy in joules.

In classical physics, gravity exerts a constant downward force F = on the center of mass of a body moving near the surface of the Earth. The work of gravity on a body moving along a trajectory r = , y, z), such as the track of a roller coaster is calculated using its velocity, v = , to obtain

r

Expression For Gravitational Potential Energy At Height Derive U = Mgh

If a body is taken from the surface of the earth to a point at a height h above the surface of the earth, then ri = R and rf = R + h then,

U = GMm

U = GMmh/R

When, h< < R, then, R + h = R and g = GM/R2.

On substituting this in the above equation we get,

Gravitational Potential Energy U = mgh

Note:

• The weight of a body at the centre of the earth is zero due to the fact that the value of g at the centre of the earth is zero.
• At a point in the gravitational field where the gravitational potential energy is zero, the gravitational field is zero.

Also Check: Algebra And Trigonometry 3rd Edition Stewart Pdf Free

Can Someone Explain The Difference Between Mgh And

I’m a bit confused since I learnt earlier that potential energy is mgh but now I learn that it is also -GMm/r?

Note that g is the acceleration of gravity and is a constant in U = mgh. As a constant, that equation is only valid where h is small compared to r and we can ignore differences in the free-fall acceleration of gravity.

Lets use

U = -G M m / r

to find the difference in potential energy between

r = R

where R is the radius of our planet. We get:

DeltaU = G m M – 1 / R )

and we can re-write the stuff in the parentheses as

1 / – 1 / R = / R = h / .

Because

we can make the approximation

R2 + R h ~ R2 ,

-h / ~ -h / R2

DeltaU = -G m M h / R2 .

Now, if we combine Newtons formula for classical gravitation,

F = G M m / r2

with his second law,

we find that the free-fall acceleration of gravity is

a = G M / r2

which we often call g with the convention that the acceleration is in the negative r direction which we can then substitute into our equation above to give

DeltaU = m g h

which is the same answer as we got using the old

U = m g h

equation for a change in height from h to 0.

Gravitational Potential Of A Spherical Shell

Consider a thin uniform spherical shell of the radius and mass situated in space. Now,

Case 1: If point P lies Inside the spherical shell :

As E = 0, V is a constant.

The value of gravitational potential is given by, V = -GM/R.

Case 2: If point P lies on the surface of the spherical shell :

On the surface of the earth, E = -GM/R2.

Using the relation

Gravitational Potential = -GM/R.

Case 3: If point P lies outside the spherical shell :

Outside the spherical shell, E = -GM/r2.

Using the relation

V = -GM/r.

Don’t Miss: Mode In Math Terms

Potential Energy $= Mgh$ What Is $h$

NOTE: when I say potential energy I mean gravitational PE

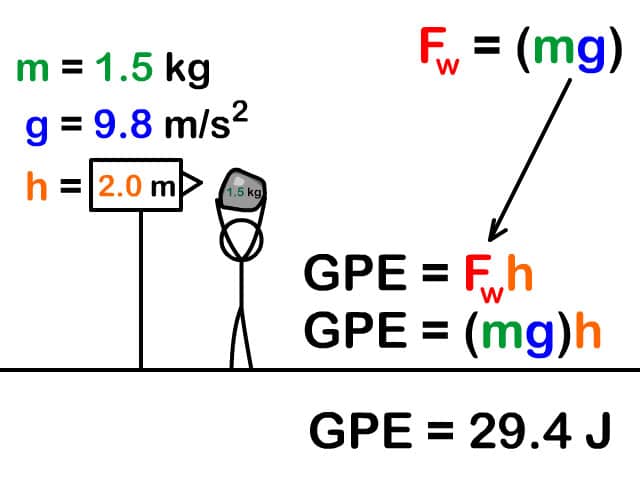
The formula for potential energy is P.E = mgh.

What is h referring to? Height, obviously.

Consider the example: What is the potential energy of a 1kg mass lifted 2 metres off the ground?

m=1, g=9.8, h=2 => P.E=17.6J

My problem is this: why is h the height off the ground, this seems rather arbitrary. Would it not make more sense to have h as the height from the centre of gravity?

Suppose we repeat the experiment on top of a mountain, does the mass still have the same potential energy? I am pretty sure it doesn’t.

I am foreseeing one or both of the following answers, so which one will it be?

I am leaning towards the first one, but I am still generally uncomfortable with the idea that you can’t have an absolute P.E

• Kyle KanosDec 30, 2014 at 3:19
• $\begingroup$@KyleKanos Nothing I suppose.. But if you take h to be the distance from the centre of mass of the earth to the object can’t you have an absolute PE?$\endgroup$ lagrange103Dec 30, 2014 at 3:21
• $\begingroup$GPE represents the work required to move an object from one height to another, so it’s really a “difference” that matters.$\endgroup$

It’s the first one. This is a really excellent observation! It’s a fascinating fact of physics.

EDIT:

$F = – \frac.$

Here’s the payoff:

Gravitational Potential Of A Uniform Solid Sphere

Consider a thin uniform solid sphere of the radius and mass situated in space. Now,

Case 1: If point P lies Inside the uniform solid sphere :

Inside the uniform solid sphere, E = -GMr/R3.

Using the relation

The value of gravitational potential is given by,

V = -GM

Case 2: If point P lies on the surface of the uniform solid sphere :

On the surface of a uniform solid sphere, E = -GM/R2. Using the relation

V = -GM/R.

Using the relation over a limit of we get, V = -GM/R.

Case 4: Gravitational potential at the centre of the solid sphere is given by V = × .

You May Like: Geometry Holt Textbook Answers

Kinetic And Gravitational Potential Energy

Learn about kinetic and gravitational potential energy.

Any object lifted above the ground has gravitational potential energy or GPE).

The amount of gravitational potential energy an object has on Earth depends on its:

• mass

• all the books on a shelf have GPE
• books A and B have more GPE than book C because they are higher
• book B has more GPE than book A because it has a greater mass

What Is Gravitational Potential Energy

Potential Energy is the stored energy of an object given its position relative to a body.Gravitational potential energy is one type of potential energy and is equal to the product of the object’s mass , the acceleration caused by gravity , and the object’s height as distance from the surface of the ground .

In this example, a 3 kilogram mass, at a height of 5 meters, while acted on by Earth’s gravity would have147.15 Joules of potential energy, PE = 3kg * 9.81 m/s2 * 5m = 147.15 J.

9.81 meters per second squared is widely accepted among scientists as a working average value for Earth’s gravitational pull. This figure is based on a measure of gravity at sea level at a latitude of 45°.

• At higher altitudes, gravity decreases slightly.
• The effect of latitude on gravitational force is relevant as gravity increases with increasing distance from the Equator. At the Equator, the Earth’s gravity is 9.780 m/s2 and at the poles it is 9.832 m/s2 .

Gravitational acceleration for other planets and bodies in the solar system is as follows:

Don’t Miss: Core Connections Algebra Answers

Potential Energy For A Linear Spring

A horizontal spring exerts a force F = that is proportional to its deformation in the axial or x direction. The work of this spring on a body moving along the space curve s = , y, z), is calculated using its velocity, v = , to obtain

txxxvxx

The function

Elastic potential energy is the potential energy of an elastic object ” rel=”nofollow”> bow or a catapult) that is deformed under tension or compression ” rel=”nofollow”> stressed in formal terminology). It arises as a consequence of a force that tries to restore the object to its original shape, which is most often the electromagnetic force between the atoms and molecules that constitute the object. If the stretch is released, the energy is transformed into kinetic energy.

Derivable From A Potential

In this section the relationship between work and potential energy is presented in more detail. The line integral that defines work along curve C takes a special form if the force F is related to a scalar field so that

CABAB

Potential energy U = is traditionally defined as the negative of this scalar field so that work by the force field decreases potential energy, that is

In this case, the application of the del operator to the work function yields,

FFUFx

Read Also: How To Convert In Chemistry

Derivation Of Gravitational Potential Energy Equation

Consider a source mass M is placed at a point along the x-axis, initially, a test mass m is at infinity. A small amount of work done in bringing it without acceleration through a very small distance is given by

dw = Fdx

Here, F is an attractive force and the displacement is towards the negative x-axis direction so F and dx are in the same direction. Then,

dw = dx

Since the work done is stored as its potential energy U, therefore gravitational potential energy at a point which is at a distance r from the source mass is given by

U = -GMm/r

If a test mass moves from a point inside the gravitational field to the other point inside the same gravitational field of source mass, then the change in potential energy of the test mass is given by

U = GMm

Check: Acceleration due to Gravity

Using Potential Energy To Simplify Calculations

The equation size 12 } = ital “mgh”} applies for any path that has a change in height of h h size 12 , not just when the mass is lifted straight up. It is much easier to calculate mgh mgh size 12 than it is to calculate the work done along a complicated path. The idea of gravitational potential energy has the double advantage that it is very broadly applicable and it makes calculations easier. From now on, we will consider that any change in vertical position h is accompanied by a change in gravitational potential energy mgh mgh size 12 , and we will avoid the equivalent but more difficult task of calculating work done by or against the gravitational force.

Read Also: Is Physics Or Chemistry Harder

Question About The Calculation Of Potential Energy

While taking my physics classes, I used to think that the formula mgh calculates the gravitational potential energy of a single object h distance off the ground.

Recently, I learned however that it is unreasonable to talk about the gravitational potential energy of a single object. So mgh actually calculates the gravitational potential energy of the system made up of the earth and ball.

This however gave me some confusion about the derivation of mgh.

the change in the potential energy = –

I can consider lifting a ball off the ground to a height h.

While I lift the ball, the earth exerts a gravitational force of mg downwards and the ball has a displacement of h upwards.

The dot product of force and displacement is -mgh.

So consequently the change in the potential energy of the earth and ball is – or mgh.

In the previous example, we considered the case in which the earth exerts a force on the ball.

We should be able to get the same answer if we consider the case in which the ball exerts a force on the earth.

the change in the potential energy = –

I can consider lifting a ball off the ground to a height h.

While I lift the ball, the ball exerts a gravitational force of mg upwards and the earth has a displacement of 0.

The dot product of force and displacement is 0.

So consequently the change in the potential energy of the earth and ball is 0.

I’m not sure what I did wrong here.

Any help would be appreciated.

OK. So let’s look at your analysis step by step:

Can Work Be Negative

The answer to the question can work be negative? is yes.When a forceoperating on a body displaces it in the direction of a force, work is done. When a force of 1 Newton is exerted over a distance of 1 meter, the work done by a moving object equals 1 Joule Because the applied force can be either negative or positive, work can also be either negative or positive.Negative work may be seen in the motion of a body against a force of friction.

Also Check: Paris Jackson Mark Lester

What Is Instantaneous Velocity

The velocity of an object at any single instant or point is called instantaneous velocity.It is similar to average velocity, except the time interval is infinitely small.The formula for instantaneous velocity is the limit as the time approaches zero of the change in displacement over the change in time.

How Is Gravitational Potential Energy $mgh$

I know the derivation that $W=Fd$, hence $F=mg$ and $d=h$ so energy gained by the body is $mgh$ considering the body on the ground to have $0$ gravitational potential energy.

But the definition of work is

Work done is the product of force and displacement caused by it in the same direction.

That means work done on a body to lift it against gravity to a certain height should be equal to the potential energy gained by it, right? My book also states that:

$mg$ is the minimum force required to lift a body against earth’s gravity.

But how does that make sense? Suppose a body is kept on the ground, and we apply a force$mg$ on it, won’t the force of gravity and this external force cancel out and ultimately result in no movement of the body? How is the derivation of $U=mgh$ thus obtained?

Part of the problem is to distinguish between the work done by a particular force and the net work done by all the forces. The second is to notice that the work done on an object depends on the process undergone. The third is to understand that the relationship between work and potential energy is that the work done by a conservative force is proportional to the change in the potential energy.

Let’s walk through the scenario. A block of mass $m$ sits on the ground at position $y=0$. There are two forces acting: the gravitational force downward and then normal force upward. Newton’s 2nd Law tells us that$$m\vec=\vec_} =\vec_}+\vec_}\,.$$We’ll abbreviate these as $\vec_}$, $\vec_}$, and $\vec$.

Read Also: Which Of The Following Perspectives Dominated American Psychology For Decades

Work And Potential Energy

Potential energy is closely linked with forces. If the work done by a force on a body that moves from A to B does not depend on the path between these points , then the work of this force measured from A assigns a scalar value to every other point in space and defines a scalar potential field. In this case, the force can be defined as the negative of the vector gradient of the potential field.

If the work for an applied force is independent of the path, then the work done by the force is evaluated from the start to the end of the trajectory of the point of application. This means that there is a function U, called a “potential,” that can be evaluated at the two points xA and xB to obtain the work over any trajectory between these two points. It is tradition to define this function with a negative sign so that positive work is a reduction in the potential, that is

CC

The function U is called the potential energy associated with the applied force. Examples of forces that have potential energies are gravity and spring forces.

What Is Gravitational Potential

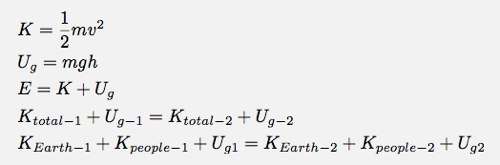
The amount of work done in moving a unit test mass from infinity into the gravitational influence of source mass is known as gravitational potential.

Simply, it is the gravitational potential energy possessed by a unit test mass

V = U/m

• The gravitational potential at a point is always negative, V is maximum at infinity.
• The SI unit of gravitational potential is J/Kg.
• The dimensional formula is M0L2T-2.

You May Like: Hawkes Learning Systems Answer Key College Algebra