How To Do Math In Python

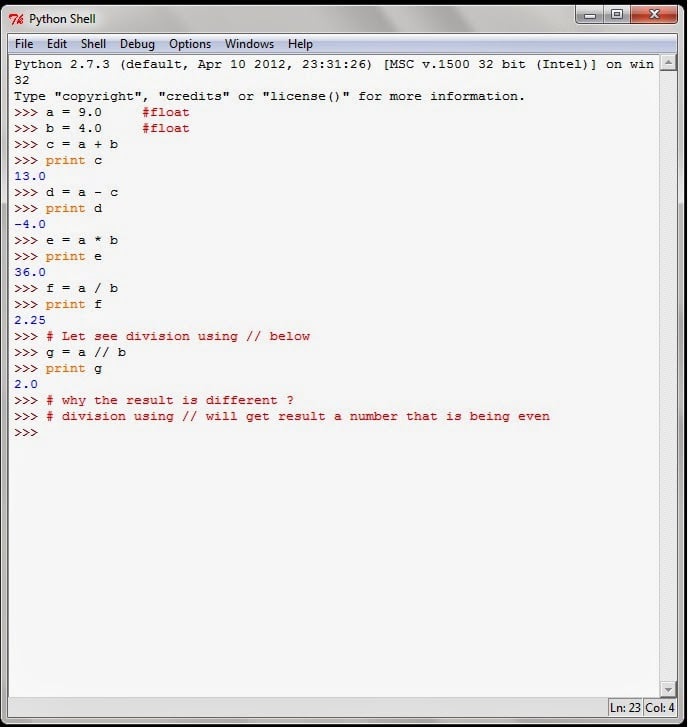
Rational And Complex Numbers Are Native Citizens

We can throw in rational or complex numbers as easily as floating-point numbers into the mix. For this, we need to use a magic function mpmathify which works with sympy internals to interpret those quantities.

We dont have to import Python modules like fraction or cmath to work with such quantities at a precision of our choice.

Learn about all other general utility functions that mpmath offers here.

Using The / Operator In Python

The / operator is used to divide one or more numeric values in Python. This operator deviates in behavior from the +, -, and * operators, in that, no matter which type of value you divide, it always returns a float. This means that even if you divide two int values, you still get a float. Try out the following code to see this in action:

integerValueOne = 208integerValueTwo = 104totalValue = integerValueOne / integerValueTwoprint 

When you run the above code, you can see that instead of an integer value, you get a float: 2.0.

Operators For Integer Math In Python

Great, those were all the basics, lets take a look at some less intuitive operators. In traditional math, these are used only on integers. In Python, you can actually use these on floats too but you may not get an exact answer. The operators well look at in this section are integer divide , modulo , and exponent . The modulo operator gives you the remainder of `a%b`, and the exponent operator, `a**b`, will give you `a` raised to the `b` power.

def integer_divide:    return a//bdef modulo:    return a%bdef exponent:    return a**b

Also Check: Algebra Nation Answers Section 9

Operator Order Of Precedence In Python

When we perform math in Python, as in real life, equations are read in what is known as order of precedence. This means that certain operators get evaluated before others. In Python, the *, /, //, and % operators have the highest precedence . They get evaluated prior to + and operators, which have lower precedence.

We can force the order that we want equations to be evaluated in Python by encasing them in parentheses . To see how this works and why it matters, enter the following code into your IDE and run it to see the difference order of precedence makes:

regularOrder = 4 * 4 - 2 + 2forcedOrder = 4 * 4 - print print 

Even thoough these equations look the same, their outcome is completely different. Running this program results in the following output:

1612

Using Python On University Machines

A number of Python tools are available on a standard university desktopmachine. We will mostly be using Python through spyder, which allows usto write, run, test and debug python code in one place. To launchspyder, either type spyder in the search bar, or go to Start,then AllPrograms, then ProgrammingLanguages, thenAnaconda, then choose spyder.

Also Check: How Does Geography Affect Our Lives

Different Math Functions In Python

All key mathematical functions are deeply described below,

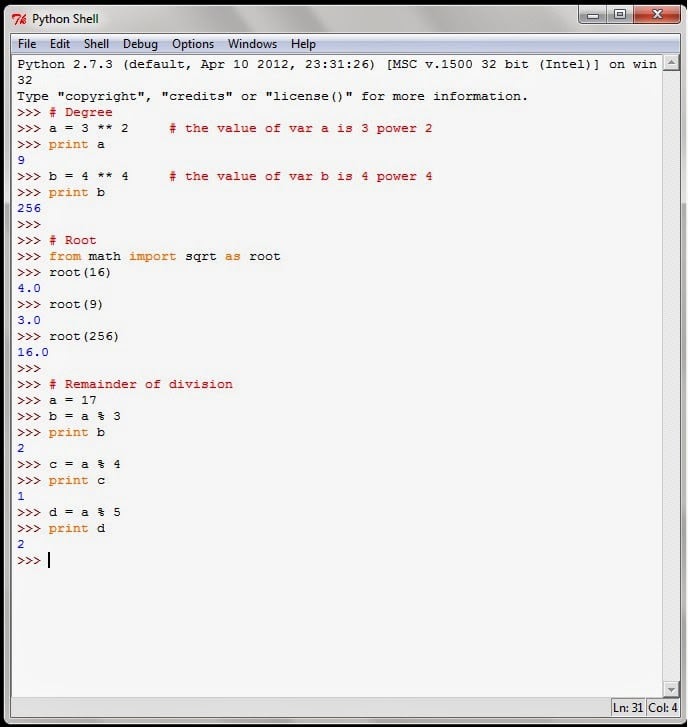
1. Constants

In the case of a mathematical constant, the value for this constant is represented by an unambiguous definition these definitions, at some instances, are represented by means of any special symbols or by many famous mathematicians names or by any other popular means. Constants occur within numerous areas of mathematics by means of constants such as and e happening in miscellaneous circumstances like number theory, geometry, and calculus.

The meaning of a constant to arise naturally and makes a constant interesting is in due course material of need, and a number of mathematical constants are prominent more for chronological grounds than by means for their fundamental mathematical interest. The more well-liked constants comprise been studied all the way through the ages and computed to a lot of decimal places.

Example :

import mathprintprintprintprintprint

Output :

2. Logarithmic Functions

The inverse for exponentiation is called as a logarithm. For any given number x, in order for determining its respective logarithm value, the exponent of another fixed number with base b is calculated. In a more straightforward case, the logarithm calculates or counts the numeral occurrences of the same factor in repeated multiplication

Ex: 1000 = 10×10×10 = 103, then the logarithm to base 10 of 1000 is 3.The logarithm of x to base b is denoted as logb.

Ex : 82 = 8 × 8 = 64

Example:

Two Objects Can Be Touching And Yet Moving Away From Each Other Use Limits To Find These Remove Them From The List Of Colliding Objects

How do we detect if two circles are moving toward each other? I originally thought we could just check their relative speed. The relative speed, however, of the red circle is the same in these two situations. In the first they are moving toward each other and in the second they are not.

A better approach is to see if the centers are getting closer together. But when? They may start by getting closer but later move away from each other. Might we ask if they are getting closer at time zero? That doesnt work because at any moment in time, their distance is unchanging.

The solution is to again use limits. Well test if in the instant after time zero, they are getting closer.

from sympy import symbols, limit, sqrtfrom perfect_physics import savea_x, a_y, a_vx, a_vy, b_x, b_y, b_vx, b_vy, t = symbolsd0 = sqrt ** 2 +  ** 2)d1 = sqrt) ** 2 + ) ** 2)speed_toward =  / tinstant_speed = limitsave

In the first example above, applying the resultant formula returns 1. In the second example, it returns -1. Both results are as expected.

To see if a circle is moving toward a wall, we find , the point on the wall where the circles center might hit. That requires four equations that can be solved with SymPy linsolve. We then use the instant_speed formula that we just found to see how fast the circle is moving towards or away from that point:

For example, for this situation we find the circle is moving toward the wall at speed sqrt.

Also Check: What Is The Definition Of Potential Energy In Physics

Using The Custom Sqrt Function

You can write your sqrt function without importing any external libraries. The square root of num can be easily calculated using the code num**0.5.

Remember to check for typos and to declare the function before using it.

# Declare the sqrt functiondef sqrt:  return num ** 0.5# Then, use the sqrt functionprint)

Output:

3.0

How to avoid getting NameError in the future?

Making your code well-organized and easy to read is one of the most important things you can do to avoid NameErrors. Use clear variable and function names, and comment on your code. These things will help you in detecting errors early before they cause problems.

Using The * Operator In Python

The * operator is used to multiply numeric values in Python. Again, anytime you multiply a value by a floating-point number, the end result will be a float. Here is how you use the * operator on numbers in Python:

integerValue = 204decimalValue = 104.2totalValue = integerValue * decimalValueprint 

This quick code snippet would result in the return of the value: 21256.8.

Don’t Miss: What Is Density In Physics

Practical Example With Exp

Radioactive decay happens when an unstable atom loses energy by emitting ionizing radiation. The rate of radioactive decay is measured using half-life, which is the time it takes for half the amount of the parent nucleus to decay. You can calculate the decay process using the following formula:

You can use the above formula to calculate the remaining quantity of a radioactive element after a certain number of years. The variables of the given formula are as follows:

• N is the initial quantity of the substance.
• N is the quantity that still remains and has not yet decayed after a time .
• T is the half-life of the decaying quantity.
• e is Eulers number.

Scientific research has identified the half-lives of all radioactive elements. You can substitute values to the equation to calculate the remaining quantity of any radioactive substance. Lets try that now.

The radioisotope strontium-90 has a half-life of 38.1 years. A sample contains 100 mg of Sr-90. You can calculate the remaining milligrams of Sr-90 after 100 years:

> > > half_life=38.1> > > initial=100> > > time=100> > > remaining=initial*math.exp> > > f"Remaining quantity of Sr-90: "'Remaining quantity of Sr-90: 16.22044604811303'

As you can see, the half-life is set to 38.1 and the duration is set to 100 years. You can use math.exp to simplify the equation. By substituting the values to the equation you can find that, after 100 years, 16.22mg of Sr-90 remains.

However, the function returns a ValueError if you input a non-positive number:

Using The Math Module In Python

math is a built-in module in the Python 3 standard library that provides standard mathematical constants and functions. You can use the math module to perform various mathematical calculations, such as numeric, trigonometric, logarithmic, and exponential calculations.

This tutorial will explore the common constants and functions implemented in the math module and how to use them.

Also Check: What Is High School Level Math

Introduction To Math Functions In Python

In Python, Math functions are a collection of pre-defined mathematical actions with generic implicit values that can be directly fetched for the mathematical operations in the program. There are several such math functions in python, like constants , logarithmic functions returns e**x), expm1 returns e**x-1, log2 returns logarithmic value for x with base2, sqrt returns square root value for x), numeric functions , isinf, remainder returns value of remainder for dividing x by y) and trigonometric functions , cos, tanx).

Counting With A While Loop

Here is an example showing when its useful to use counters

> > >  i = 0> > >  while i <  5:...     print i...     i =  i + 1... 01234

The program counts from 0 to 4. Between the word while and the colon, there is an expression that at first is True but then becomes False.

As long as the expression is True, the following code will run.

The code that needs to be run has to be indented.

The last statement is a counter that adds 1 to the value for everytime the loop runs.

Also Check: What Is Entropy In Chemistry

Using The + Operator In Python

The + operator in Python is used for addition at least when it is used on integers or floating-point numbers. When used on strings it does something else entirely. For now, we are going to focus on its use on numeric values.

You can add one or more numbers using the + operator, as you might suspect. The code for its use is simple enough:

104 + 104

Typing the above into the Python Shell would return the result of 104 plus 104, or, 208. Simple math. The same goes if you were to add two floats:

104.1 + 104.1

Typed into the Python Shell, the above equation would result in 208.2. Again, nothing magical going on here.

Where things begin to differ, however, is when we add an int and a float together. When we do this, no matter what, the returned value is always a float. Try the following code in your IDE:

integerValue = 104decimalValue = 104.2totalValue = integerValue + decimalValueprint 

Here, we create two variables: one holds an integer, the other a floating-point number. We then create a new variable called totalValue and assign it the sum of integerValue and . The result is: 208.2.

How To Do Python Math At Command Line

In this article, we will show you how to do python math at the command line.

Python is an interpreter-based language. When you invoke the Python interpreter, Python prompt appears. Any Python statement can be entered in front of it.

As soon as you press ENTER, the statement is executed. Hence a mathematical expression using operators defined in Python will be evaluated at the command line.

Recommended Reading: What Is Linguistic Determinism In Psychology

Doing Some Math In Python With Code Examples

Doing Some Math In Python With Code Examples

In this tutorial, we will try to find the solution to Doing Some Math In Python through programming. The following code illustrates this.

a_number = 3the_complete_number = a_number + a_number #result should be 6the_the_complete_number = a_number * a_numner #result should be 9the_the_the_complete_number = a_number - a_number #result should be 0

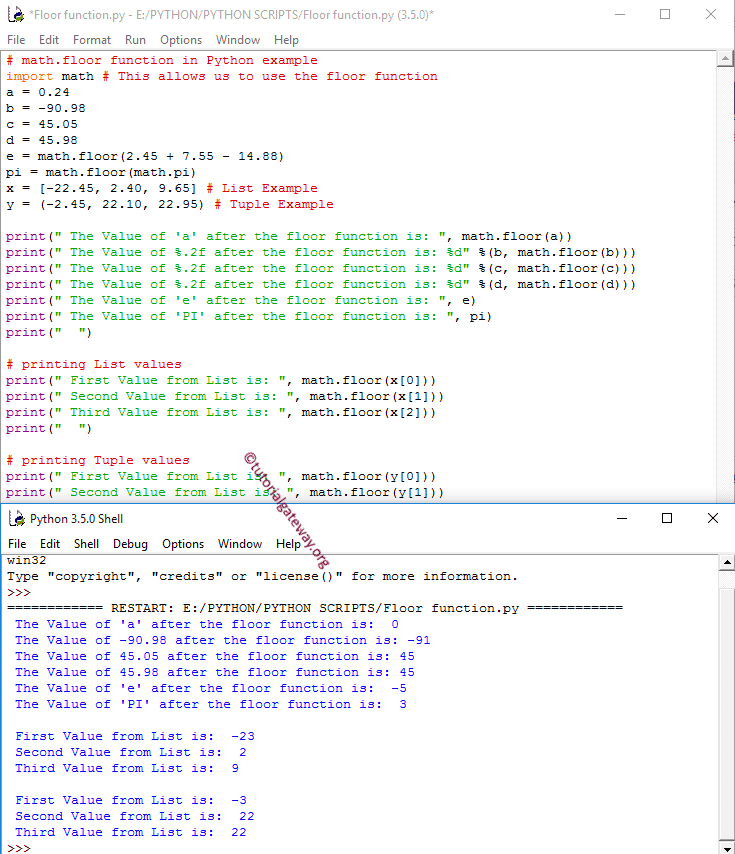
The Math Module Functions

The math module provides a wide range of mathematical functions for many different scientific and engineering applications, including the following:

• Number functions

The math.floor method maps a floating-point number to the greatest preceeding integer:

q = 9.99print)

9

math.factorial

The math.factorial method returns the product of all natural numbers less than or equal to n, if n a positive integer. However, if n = 0, it returns 1. The code below uses the math.factorial to calculate $5!$:

n = 5print))

5! = 120

math.gcd

The math.gcd method returns the greatest common denominator for two numbers we can use it to reduce fractions.

For example, the GCD for 25 and 120 is 5, so we can divide the numerator and denominator by 5 to get a reduced fraction . Lets see how it works:

gcd = math.gcdprint

5

math.fabs

The math.fabs method removes the negative sign of a given number, if any, and returns its absolute value as a float:

print)

Read Also: What Is Accommodation In Psychology

Sign Up For Pythonanywhere

First you need to get python to run your code. You can actually download python for free, without signing up for pythonanywhere, but pythonanywhere is really accessible and easy for beginners. There are also payed versions of pythonanywhere, but these aren’t necessary.

Start by going to pythonanywhere.com and click the tab in the upper right hand corner that says “Pricing & signup”, next click the button that says “create a Beginner account”.

Follow the steps to create an account and you can take the tour that they provide to better understand the layout if you like.

Most Used Python Math Functions

You May Like: What Is Mm In Chemistry

Solving Math Problems Using Python

This is the second chapter of the Quick Code-Python series, to recap the last blog weve seen how to assign values to a variable, operation precedence, how BODMAS helps python calculate equations, variable names that we can and cannot use, and also different data types available in python. to check that out.

Note: Ive written the Quick Code-Python series in a linear fashion so that even a newbie can follow along the series to get a grasp of what python can actually do. For folks that are good with the fundamentals, you can follow along with the series to refresh your concepts or choose any of the chapters in the series that you want to know more about.

In this blog, were going to put all the theories into practice. There are some fun problems that we could easily solve using python. The main goal of this blog is to be able to convey how easy and simple it is to get results for a problem using python.

A. Calculating the Area and Perimeter of a Rectangle

Area of a rectangle: a*b

Perimeter of a rectangle: 2*

a = 2

printO/P : 0 # number is evena = 7b = 2c = a%bprintO/P : 1 # number is odd

We can, of course, add some lines in the print statement saying the number is even or odd but for now, just for understanding purposes Ill put them in a comment line

D. takes a number and squares it. take the square root of the result you get from the task

E. Calculate the area and volume of the Cube.

Area of a Cube : 6*a*a

Volume of a Cube : a*a*a

a = 30

How To Convert Between Integer And Float In Python

Python has two functions that let you convert between int and float values. Neither of them permanently changes the value of the variable holding the integer or floating-point number mind you. Instead, you can use it to convert an instance of the variable in a different format.

These functions are int and float.

Here is an example showing the int function in Python being used to convert a float to an integer:

As you can see from the output below, the value of never actually changes it remains the same after we use int to create an instance of it. Here is the output:

Here is the original value of our variable as a float:  108.0Here is the value converted to an int: 108Here is the current value of our variable, showing no change in type:  108.0

The function float works in the same way, converting an integer into an instance of a floating-point number. Here is how that looks in code:

integerValue = 108print print print) print 

Here is the result of running this code:

Here is the original value of our variable as a float:  108Here is the value converted to an int: 108.0Here is the current value of our variable, showing no change in type:  108

Also Check: How To Make Someone Miss You Psychology

Truncate Numbers With Trunc

When you get a number with a decimal point, you might want to keep only the integer part and eliminate the decimal part. The math module has a function called trunc which lets you do just that.

Dropping the decimal value is a type of rounding. With trunc, negative numbers are always rounded upward toward zero and positive numbers are always rounded downward toward zero.

Here is how the trunc function rounds off positive or negative numbers:

> > > math.trunc12> > > math.trunc-43

As you can see, 12.32 is rounded downwards towards 0, which gives the result 12. In the same way, -43.24 is rounded upwards towards 0, which gives the value -43. trunc always rounds towards zero regardless of whether the number is positive or negative.

When dealing with positive numbers, trunc behaves the same as floor:

> > > math.trunc==math.floorTrue

trunc behaves the same as floor for positive numbers. As you can see, the return value of both functions is the same.

When dealing with negative numbers, trunc behaves the same as ceil:

> > > math.trunc==math.ceilTrue

When the number is negative, floor behaves the same as ceil. The return values of both functions are the same.