The Relationship Between Enthalpy And Entropy:
The relationship between enthalpy and entropy can be seen to calculate the Gibbs free energy. Josiah Willard Gibbs developed Gibbs energy in the 1870s. He termed it as available energy of a system that can be used to do work. It is defined as the sum of the enthalpy of a system and the product of the entropy and temperature of the system. It is denoted as G.
G = H + TS
Introduction To Enthalpy Vs Entropy
When you get to the thermodynamics section of AP® Chemistry, one of the hardest things to remember is the definition of enthalpy vs. entropy. This tutorial explains the theory behind enthalpy and entropy using the laws of thermodynamics. Then we will talk about the definition of enthalpy and how to calculate it using enthalpy practice questions. Once you have a firm hold on the definition of enthalpy, we will discuss entropy and look at entropy practice questions. Finally, we will revisit the topic of Gibbs free energy, of which you should already have a decent understanding, and how it relates to enthalpy vs. entropy.
The Discovery Of Entropy
The identification of entropy is attributed to Rudolf Clausius , a German mathematician and physicist. I say attributed because it was a young French engineer, Sadi Carnot , who first hit on the idea of thermodynamic efficiency however, the idea was so foreign to people at the time that it had little impact. Clausius was oblivious to Carnots work but hit on the same ideas.
Clausius studied the conversion of heat into work. He recognized that heat from a body at a high temperature would flow to one at a lower temperature. This is how your coffee cools down the longer its left out the heat from the coffee flows into the room. This happens naturally. But if you want to heat cold water to make the coffee, you need to do work you need a power source to heat the water.
From this idea comes Clausiuss statement of the second law of thermodynamics: heat does not pass from a body at low temperature to one at high temperature without an accompanying change elsewhere.
Clausius also observed that heat-powered devices worked in an unexpected manner: Only a percentage of the energy was converted into actual work. Nature was exerting a tax. Perplexed, scientists asked, where did the rest of the heat go and why?
Clausius solved the riddle by observing a steam engine and calculating that energy spread out and left the system. In The Mechanical Theory of Heat, Clausius explains his findings:
Also Check: Algebra 1 Eoc 2015
What Is Entropy And Why Do We Care
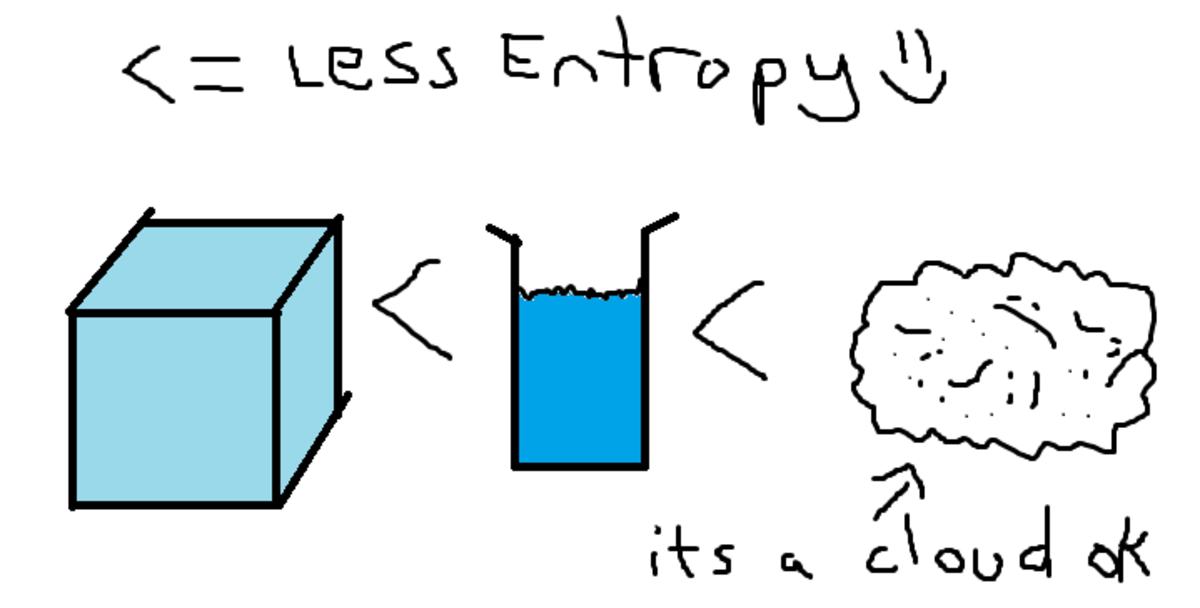
A lot of folks may describe entropy as “chaos” or “disorder”. While those descriptors are not entirely inaccurate or wrong, they are best suited as a general guide.
When quantifying entropy, entropy is better defined as the number of states available. In other words, at the molecular level, how many configurations can the molecules and atoms have?
There are other definitions or ideas associated that definition, but I will focus on the implications associated with spontaneous processes.
Another quantity called Gibb’s Free Energy is guided by entropy and energy . When Gibb’s Free Energy decreases a process will be spontaneous. In other words, the process does not require outside help to happen.
As such, to be able to predict if a process is spontaneous, you need to understand what happens to both energy AND entropy. For entropy, thinking about the states, possibilities, configurations, etc… enables you to predict if entropy will increase or decrease.
Example: imagine a can of soda . When it is opened, it will eventually go flat. From an entropic perspective, while mixtures provide more configurations than pure substances, the CO2 can arrange themselves in infinitely more configurations when not bound by the liquid.
Philosophy And Theoretical Physics
Entropy is the only quantity in the physical sciences that seems to imply a particular direction of progress, sometimes called an arrow of time. As time progresses, the second law of thermodynamics states that the entropy of an isolated system never decreases in large systems over significant periods of time. Hence, from this perspective, entropy measurement is thought of as a clock in these conditions.
Also Check: Molecular Geometry Of Ccl4
Are You Afraid Of Programming Interviews
Get proper guidance from Coding Ninjas and clear interviews of top companies like Amazon, Facebook, and Google.
| veenanandi 550 |
The most fundamental concept of information theory is the entropy. The entropy is defined asaverage amount of information per message. The entropy of a random variable X is defined by,
H =-x P log p
H 0, entropy is always non-negative. H=0 if X is deterministic.
- Since Hb = logbHa, we dont need to specify the base of the logarithm.
- The entropy is non-negative. It is zero when the random variable is certain to bepredicted. Entropy is defined using the Clausius inequality.
- Entropy is defined in terms of probabilistic behavior of a source of information. Ininformation theory the source output are discrete random variables that have a certain fixedfinite alphabet with certain probabilities. Entropy is average information content for thegiven source symbol.
- Entropy : Binary memory less source has symbols 0 and 1 which have probabilitiesp0 and p1 . Count the entropy as a function of p0.
- Entropy is measured in bits
There are two types of Entropy:
Joint Entropy:
Joint entropy is entropy of joint probability distribution, or a multi valued random variables. If Xand Y are discrete random variables and f is the value of their joint probability distribution of, then the joint entropy of X and Y is
H=- x X y Y f log f
Conditional Entropy:
H =-xXy Y f log fis the conditional entropy of Y given X.
Thermodynamic Definition Of Entropy
Using the statistical definition of entropy is very helpful to visualize how processes occur. However, calculating probabilities like \ can be very difficult. Fortunately, entropy can also be derived from thermodynamic quantities that are easier to measure. Recalling the concept of work from the first law of thermodynamics, the heat absorbed by an ideal gas in a reversible, isothermal expansion is
If we divide by T, we can obtain the same equation we derived above for \:
We must restrict this to a reversible process because entropy is a state function, however the heat absorbed is path dependent. An irreversible expansion would result in less heat being absorbed, but the entropy change would stay the same. Then, we are left with
for an irreversible process because
This apparent discrepancy in the entropy change between an irreversible and a reversible process becomes clear when considering the changes in entropy of the surrounding and system, as described in the second law of thermodynamics.
It is evident from our experience that ice melts, iron rusts, and gases mix together. However, the entropic quantity we have defined is very useful in defining whether a given reaction will occur. Remember that the rate of a reaction is independent of spontaneity. A reaction can be spontaneous but the rate so slow that we effectively will not see that reaction happen, such as diamond converting to graphite, which is a spontaneous process.
You May Like: Movement Geography Example
What Gets Stored In A Cookie
This site stores nothing other than an automatically generated session ID in the cookie no other information is captured.
In general, only the information that you provide, or the choices you make while visiting a web site, can be stored in a cookie. For example, the site cannot determine your email name unless you choose to type it. Allowing a website to create a cookie does not give that or any other site access to the rest of your computer, and only the site that created the cookie can read it.
What Is The Enthalpy Change
An enthalpy change is defined as the difference between the energy gained by the formation of new chemical bonds and the energy used to break bonds in a chemical reaction at constant pressure. In simple terms, it tells about the amount of heat evolved or absorbed during a reaction. It is denoted as H. It is expressed as follows:
H = U +PV
Read Also: Geometry Basics Unit 1 Test
Wrapping Up Enthalpy Vs Entropy
The definition of enthalpy vs. entropy should be much clearer now. If you have any other questions or comments about enthalpy vs. entropy, please let us know in the comments below! If you would like more practice with enthalpy vs. entropy problems, we have included more practice problems and their answers below.
Enthalpy Practice Problems
1. The standard enthalpy of formation of AgNO_ is -123.02 \text. What is the standard enthalpy of formation of AgNO_, given the following reaction?
_\rightarrow _+\dfrac _
2. Given the following standard enthalpies of formation, calculate the heat of combustion per mole of gaseous water formed during the combustion of ethane gas.
__+_\rightarrow _+__
- C_2H_: -84.68
- H_2O_: -241.8
Entropy Practice Problems
1. Which of these substances should have a higher entropy? Answer without calculating and assume that there is one mole of each substance at 25^\circ \text and 1 \text.
1. Hg or CO
2. CH_3OH or CH_3CH_2OH
3. KI or CaS
2. Predict the sign of the entropy change for the following reaction and use the given entropy values to calculate the change in enthalpy of the reaction at 25^\circ \text.
_+_\rightarrow __
\Delta ^ \text __=188.8 \text
\Delta ^ \text_=130.7 \text
\Delta ^ \text_=205.1 \text
Combined Practice Problems
1. Hydrogen and oxygen react to form water vapor with a \Delta S_= -88.99 \text. What are the entropy changes of the surroundings and the universe at 25^\circ \text?
_+\dfrac _\rightarrow _
Enthalpy Practice Problems Key
Ice Water And Entropy
Example of increasing entropy: Ice melting in a warm room is a common example of increasing entropy.
For example, consider ice water in a glass. The difference in temperature between a warm room and a cold glass of ice and water begins to equalize. This is because the thermal energy from the warm surroundings spreads to the cooler system of ice and water. Over time, the temperature of the glass and its contents and the temperature of the room become equal. The entropy of the room decreases as some of its energy is dispersed to the ice and water. However, the entropy of the system of ice and water has increased more than the entropy of the surrounding room has decreased.
In an isolated system such as the room and ice water taken together, the dispersal of energy from warmer to cooler always results in a net increase in entropy. Thus, when the universe of the room and ice water system has reached a temperature equilibrium, the entropy change from the initial state is at a maximum. The entropy of the thermodynamic system is a measure of how far the equalization has progressed.
Don’t Miss: Test Form 2b Answers Chapter 1
World’s Technological Capacity To Store And Communicate Entropic Information
A 2011 study in Science estimated the world’s technological capacity to store and communicate optimally compressed information normalized on the most effective compression algorithms available in the year 2007, therefore estimating the entropy of the technologically available sources. The author’s estimate that human kind’s technological capacity to store information grew from 2.6 exabytes in 1986 to 295 exabytes in 2007. The world’s technological capacity to receive information through one-way broadcast networks was 432 exabytes of information in 1986, to 1.9 zettabytes in 2007. The world’s effective capacity to exchange information through two-way telecommunication networks was 281 petabytes of information in 1986, to 65 exabytes in 2007.
The Second Law As Energy Dispersion

Energy of all types — in chemistry, most frequently the kinetic energy of molecules changes from being localized to becoming more dispersed in space if that energy is not constrained from doing so. The simplest example stereotypical is the expansion illustrated in Figure 1.
The initial motional/kinetic energy of the molecules in the first bulb is unchanged in such an isothermal process, but it becomes more widely distributed in the final larger volume. Further, this concept of energy dispersal equally applies to heating a system: a spreading of molecular energy from the volume of greater-motional energy molecules in the surroundings to include the additional volume of a system that initially had âcoolerâ molecules. It is not obvious, but true, that this distribution of energy in greater space is implicit in the Gibbs free energy equation and thus in chemical reactions.
âEntropy change is the measure of how more widely a specific quantity of molecular energy is dispersed in a process, whether isothermal gas expansion, gas or liquid mixing, reversible heating and phase change, or chemical reactions.â There are two requisites for entropy change.
Also Check: Movement Geography Definition
What Is Entropy And Enthalpy In Chemistry
4.7/5EnthalpyentropyEnthalpyentropy
Similarly, what is difference between entropy and enthalpy?
Scientists use the word entropy to describe the amount of freedom or randomness in a system. In other words, entropy is a measure of the amount of disorder or chaos in a system. Entropy is thus a measure of the random activity in a system, whereas enthalpy is a measure of the overall amount of energy in the system.
Secondly, what is a entropy in chemistry? In chemistry, entropy is represented by the capital letter S, and it is a thermodynamic function that describes the randomness and disorder of molecules based on the number of different arrangements available to them in a given system or reaction.
In this manner, what is enthalpy and entropy with example?
| Difference Between Enthalpy and Entropy | |
|---|---|
| Enthalpy | |
| Enthalpy is a kind of energy | Entropy is a property |
| It is the sum of internal energy and flow energy | It is the measurement of randomness of molecules |
| It is denoted by symbol H | It is denoted by symbol S |
What is the relation between enthalpy and entropy?
Explanation: Enthalpy is defined as the amount of energy released or absorbed during a chemical reaction. Entropy defines the degree of randomness or disorder in a system. where at constant temperature, the change on free energy is defined as: G=HTS .
Entropy In Solution Formation
For now, entropy can be thought of as molecular disorder or in terms of the energy of molecules and how spread out they are. This term increases with increasing temperature. As a molecule changes state, the general states of matter can be ordered as follows in terms of entropy: gases > liquids > solids.
In a similar manner entropy plays an important role in solution formation. Entropy commonly increases especially for ions as they transition from molecule to ions. This is because we are essentially increasing the number of particles from one compound to two or more depending upon the composition. Consider, the dissolution of sodium sulfate,
Na2SO4 > 2 Na+ + SO42-
The entropy is increasing for two reasons here:
All these factors increase the entropy of the solute. Also keep in mind that there is a loss of entropy associated with the water moleclues organizing their solvent cages around the ions themselves. This factor can sometimes lead to only a small increase in entropy although a large increase is expected. Thus, in the very common case in which a small quantity of solid or liquid dissolves in a much larger volume of solvent, the solute becomes more spread out in space, and the number of equivalent ways in which the solute can be distributed within this volume is greatly increased. This is the same as saying that the entropy of the solute increases.
Boundless.
Also Check: Evaluate Homework And Practice Workbook Answers Geometry
Relating Entropy To Energy Usefulness
Following on from the above, it is possible to regard lower entropy as an indicator or measure of the effectiveness or usefulness of a particular quantity of energy. This is because energy supplied at a higher temperature tends to be more useful than the same amount of energy available at a lower temperature. Mixing a hot parcel of a fluid with a cold one produces a parcel of intermediate temperature, in which the overall increase in entropy represents a “loss” that can never be replaced.
Thus, the fact that the entropy of the universe is steadily increasing, means that its total energy is becoming less useful: eventually, this leads to the “heat death of the Universe.”
Second Law Of Thermodynamics
According to concepts of entropy and spontaneity, the second law of thermodynamics has a number of definitions.
Stotal =Ssurroundings+Ssystem> 0
Recommended Reading: Geometry Dash Toe2
The Distribution Of Energy
To obtain some idea of what entropy is, it is helpful to imagine what happens when a small quantity of energy is supplied to a very small system. Suppose there are 20 units of energy to be supplied to a system of just 10 identical particles. The average energy is easily calculated to be two units per particle. Although this is the average energy, this state of the system can only arise if every particle has two units of energy. If all the energy were concentrated in one particle, any one of the 10 particles could take it up and this state of the system is 10 times more probable than every particle having two units each.
If the energy is shared between two molecules, half of the energy could be given to any one of the 10 particles and the other half to any one of the remaining nine particles, giving 90 ways in which this state of the system could be achieved. However, since the particles are indistinguishable, there would be only 45 ways in which this state can be achieved. Sharing the energy equally between four particles increases the number of possible ways this energy can be distributed to 210. This kind of calculation quickly becomes very tedious, even for a very small system of only 10 particles, and completely impracticable for systems where the number of particles approaches the number of atoms/molecules in even a very small fraction of one mole.
Figure 1 – Boltzmann distribution of the number of particles with energy E at low, medium and high temperatures