How To Calculate Gradient
To calculate the gradient, we will find two points. We will denote these points with the cartesian coordinates and respectively. This is also the notation used in the calculator. Note that we used the same symbols in the real-life example. We want to see how they relate to each other, that is, what is the rise over run ratio between them. It is described by the gradient formula:
gradient = rise / run
with rise = y – y and run = x – x. The rise is how much higher/lower the second point is from the first, and the run is how far they are from each other.
Determining Gradientof A Slope On Topographic Maps
Vertical Increase HorizontalEquivalent
Procedures forDetermining Gradient on Topographic Maps
Step 1: Identifythe location of the two points whose gradient is to be calculated/determined onthe map. Step 2:. Draw a straight line joining these points.Step 3: Determinethe horizontal equivalent.
| The horizontal equivalent is 4km |
Determinethe elevations of each of these points, and then calculate the VerticalIncrease
Gradient Formula: Example Of Application
Now that we know the gradient definition, it’s time to see the gradient calculator in action and go through how to use it together, step by step:
Read Also: What Does Ac Stand For In Physics
How To Calculate Slopes And Gradients
You can download a pdf of this guide by clicking on the button below.
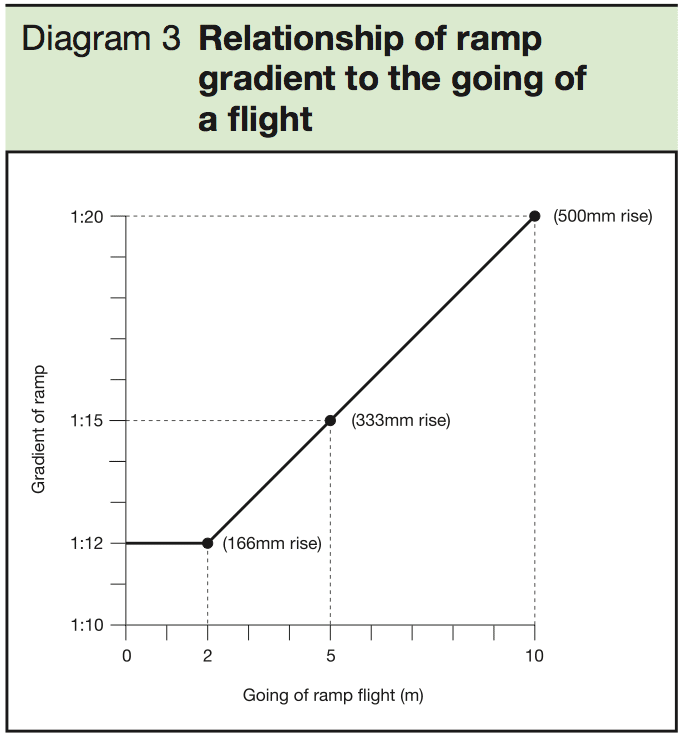
As an architect you will need to know how to calculate slopes and gradients in differing situations. The most common occurrence of this is working with ramped access to buildings, groundworks, car parks and so on. Slopes can be measured in angles, percentages and ratios. For this post I will focus on the measurement of slopes in ratios, mainly because gradient ratios are stated in the building regulations. At the end I will also take a quick look at slope percentages and how to work them out.
Approved Document Part M of the building regulations specifies limits for ramp gradients for access to a building. If access to a building is too steep it is not deemed to be a safe access and creates difficulty for people in wheelchairs who may not have the strength to propel themselves up a slope, or may have difficulty slowing down when descending a slope that is too steep. Some people find they need to stop frequently when ascending/descending ramp and therefore suitable landings are required at specified intervals to allow for this.
The table below shows the guidelines from the building regulations:
To work out the gradient of an existing slope you will need the distance of the slope and the height of the slope . The method that follows may not be the most mathematical way to work out the ratio gradient of a slope but it is really simple and has always worked for me!
How To Calculate Gradients On A Topographic Map
The first thing to remember when you want to calculate a gradient on a topographic map is that the two terms gradient and slope are interchangeable. The gradient change occurring within a specific area on the map reveals the lay of the land. In turn, this helps geologists and environmentalists determine any effect the gradient of the specified area has on areas around it. Erosion is a good example of why knowing the gradient of specific areas is important. Doing a project such as this is easier with a scientific calculator because you may need to calculate arctangents.
Place the map on a smooth surface, and choose the area where the gradient needs to be calculated. Do not choose an area that goes over a hill or down and then up a valley.
Draw a line perpendicular to the lines depicting the contours of the slope with a ruler. Begin your line on one of the contour lines and end on another one. Measure the line and translate that figure into feet, using the map legend.
Calculate the gradient by subtracting the elevation of the lower contour line on the line you drew from the elevation of the contour line at the other end of the line you drew.
Divide the answer by the distance in feet represented by the line you drew. Multiply that number by 100 to give you the percent slope of the hill. For example, if the number you arrived at was 45. This means that for every 100 feet traveled in the area marked on the map, the elevation changes 45 feet whether going up or down the hill.
Read Also: How To Pass The Sbac Math Test
What Is Average Gradient In Geography
Average Gradient: is the average/general relationship between vertical height and horizontal distance .
How do you find the average gradient of a slope?
Gradient = vertical difference in elevation / horizontal distance. So, to calculate the average gradient along the stream from the red dot at B to the red dot at A two facts need to be known: The difference in elevation between B and A. The distance along the stream from B to A.
How do you calculate the average gradient of a parabola?
Method: Average GradientWrite the equation of the curve in the form y=.Calculate y1 by substituting x1 into the equation for the curve.Calculate y2 by substituting x2 into the equation for the curve.Calculate the average gradient using: y2-y1x2-x1.
What is the average rate of change equation?
The average rate of change formula is used to find the slope of a graphed function. To find the average rate of change, divide the change in y-values by the change in x-values.
If 1 Point And The Slope Are Known
Slope, sometimes referred to as gradient in mathematics, is a number that measures the steepness and direction of a line, or a section of a line connecting two points, and is usually denoted by m. Generally, a line’s steepness is measured by the absolute value of its slope, m. The larger the value is, the steeper the line. Given m, it is possible to determine the direction of the line that m describes based on its sign and value:
- A line is increasing, and goes upwards from left to right when m > 0
- A line is decreasing, and goes downwards from left to right when m < 0
- A line has a constant slope, and is horizontal when m = 0
- A vertical line has an undefined slope, since it would result in a fraction with 0 as the denominator. Refer to the equation provided below.
Slope is essentially the change in height over the change in horizontal distance, and is often referred to as “rise over run.” It has applications in gradients in geography as well as civil engineering, such as the building of roads. In the case of a road, the “rise” is the change in altitude, while the “run” is the difference in distance between two fixed points, as long as the distance for the measurement is not large enough that the earth’s curvature should be considered as a factor. The slope is represented mathematically as:
| m = |
| y2 – y1 |
| x2 – x1 |
d = 2 + 2
m = tan
Given the points and find the slope of the line, the distance between the two points, and the angle of incline:
| m = |
Also Check: What Is G In Chemistry
How Do You Calculate Slope In Geography
To calculate percent slope, divide the difference between the elevations of two points by the distance between them, then multiply the quotient by 100. The difference in elevation between points is called the rise. The distance between the points is called the run. Thus, percent slope equals x 100.
To Determine Percent Of Slope And Angle Of Slope
< Back
Percent of slope is determined by dividing the amount of elevation change by the amount of horizontal distance covered , and then multiplying the result by 100. The “run” assumes you’re traveling on an idealized flat surface it does not account for the actual distance traveled once elevation change is factored in.
Example: lets assume your climb gains 1,000 feet in altitude and the horizontal distance as measured on the map is 2,000 feet .
1,000 divided by 2,000 equals 0.5Multiply 0.5 by 100 to derive percent of slope: 50%
Example: lets assume your climb gains 500 feet in altitude and the horizontal distance as measured on the map is 3,000 feet .
500 divided by 3,000 equals 0.166Multiply 0.166 by 100 to derive percent of slope: 16.6%
Example: lets assume your climb gains 700 feet in altitude and the horizontal distance as measured on the map is 500 feet .
700 divided by 500 equals 1.4Multiply 1.4 by 100 to derive percent of slope: 140%
Angle of slope represents the angle thats formed between the run and your climbs angular deviation from that idealized flat surface. To calculate this, you divide the rise divided by the run, and then obtain the inverse tangent of the result.
Example: lets assume your climb gains 1,000 feet in altitude and the horizontal distance as measured on the map is 2,000 feet .
1,000 divided by 2,000 equals .5Press the INV button on your calculator Press the TAN button on your calculatorYour angle of slope is 26.5 degrees
You May Like: Geometry Sin Cos Tan Chart
Common Misconceptions And Mistakes
You may ask yourself, “Hold on, I think I’ve seen this somewhere else. Doesn’t something similar happen when you count the slope, or the rise over run?” You’re absolutely right. All three of these concepts: gradient, slope, and rise over run describe the same thing, and don’t you worry, there is no difference between them.
You may also wonder how steep is steep that is, what does the 2 in the above example tell us. Is it a lot, or is it not? Is the pretty skier going to be impressed by this number? Well, it’s all a matter of perspective, and some may say one thing, while others will say the opposite. As a point of reference, you should remember that having a line parallel to the horizon is considered neutral here, as the gradient equals zero. When it rises , it becomes more and more like a line perpendicular to the horizon, where the slope goes to infinity when it rises .
What Is An Average
The term average has a number of different meanings. Most generally, it is a single number that is used to represent a collection of numbers. In the context of mathematics, “average” refers to the mean, specifically, the arithmetic mean. It is a relatively simple statistical concept that is widely used in many areas.
The equation below is one of the more commonly understood definitions of the average:
| Average = |
| Sum |
| Count |
where the sum is the result of adding all of the given numbers, and the count is the number of values being added. For example, given the 5 numbers, 2, 7, 19, 24, and 25, the average can be calculated as such:
| Average = |
Recommended Reading: What Does Hydrophilic Mean In Biology
How Do You Find The Average Slope On A Topographic Map
To find the slope of a feature, the horizontal distance as well as the vertical distance between two points on a line parallel to the feature need to be determined. The slope is obtained by dividing the rise over run. Multiply this ratio by 100 to express slope as a percentage.
How do you calculate a 1 in 40 fall?
It makes no difference what unit of measurement is used. Pipe fall can also sometimes be described as a gradient. To calculate the gradient, divide the vertical fall by the horizontal length of the pipe run. So in our 1 in 40 example, the calculation would be giving a gradient of 0.025.
How do you calculate a 1 in 15 fall?
Expressing Fall0.1 = 10%0.05 = 5%0.067 = 6.7% . but percentages can be hard, if not impossible, to visualise, so a more commonly encountered method of expression is as 1 in summat ratios 0.1 = 10% = 1 in 10.0.05 = 5% = 1 in 20.0.067 = 6.7% = 1 in 15.
How do you calculate the average slope of a watershed?
The average slope of a parcel is calculated using the following formula: S = 100/A, where: A. S = Average slope .
What Is Gradient
Before we take a look at the gradient definition, let’s get back to our mountain scene, and the absolutely crucial question of steepness.
Let’s say you’re skiing down a slope when The Big Question hits you. You stop and think about it before going any further. As we’ve mentioned above, all you need is two points to find the gradient, so why not be a little self-centered and choose yourself as the… well, center, that is, the point = on the plane.
Now we’re left with finding a second point, , up or down the slope. You look around you to find some particularly bushy tree or a pretty young skier. Or an old smelly one for that matter, I’m not judging.
Tell the tree or the skier to stand still while you use your handy ruler to count how much higher/lower they are from you and how far they are from you . Remember to count the distance between you two horizontally, not parallel to the slope. And there you have it! The ratio of y / x is your gradient, or the steepness of the mountain at that point.
For sticking around while you perform your quick experiment, go and buy that skier some hot chocolate, or give the tree a hug. They deserve as much.
Don’t Miss: Ways To Remember Geometry Formulas