Limitations Of Hookes Law
The ability of an object to resist deformation and restore to normal position is called elasticity. Hookes law is applied to a limited deformation known as the elastic limit. Suppose the object is compressed or extended beyond this limit. In that case, it will not restore to its original shape and will be permanently deformed.
Example : The Stretch Of A Long Cable
Suspension cables are used to carry gondolas at ski resorts. Consider a suspension cable that includes an unsupported span of 3 km. Calculate the amount of stretch in the steel cable. Assume that the cable has a diameter of 5.6 cm and the maximum tension it can withstand is 3.0 × 106 N.
Figure 4.
Strategy
The force is equal to the maximum tension, or F = 3.0 × 106 N. The cross-sectional area is r2 = 2.46 × 10-3 m2. The equation \boldsymbol = \frac\fracL_0} can be used to find the change in length.
Solution
All quantities are known. Thus,
Discussion
This is quite a stretch, but only about 0.6% of the unsupported length. Effects of temperature upon length might be important in these environments.
Figure 5.
The Spring Constant: Car Suspension Problem
A 1800-kg car has a suspension system that cannot be allowed to exceed 0.1 m of compression. What spring constant does the suspension need to have?
This problem might appear different to the previous examples, but ultimately the process of calculating the spring constant, k, is exactly the same. The only additional step is translating the mass of the car into a weight on each wheel. You know that the force due to the weight of the car is given by F = mg, where g = 9.81 m/s2, the acceleration due to gravity on Earth, so you can adjust the Hookes law formula as follows:
However, only one quarter of the total mass of the car is resting on any wheel, so the mass per spring is 1800 kg / 4 = 450 kg.
Now you simply have to input the known values and solve to find the strength of the springs needed, noting that the maximum compression, 0.1 m is the value for x youll need to use:
This could also be expressed as 44.145 kN/m, where kN means kilonewton or thousands of newtons.
Recommended Reading: Holt Geometry Answers
How To Calculate The Spring Constant
There are two simple approaches you can use to calculate the spring constant, using either Hookes law, alongside some data about the strength of the restoring force and the displacement of the spring from its equilibrium position, or using the elastic potential energy equation alongside figures for the work done in extending the spring and the displacement of the spring.
Using Hookes law is the simplest approach to finding the value of the spring constant, and you can even obtain the data yourself through a simple setup where you hang a known mass from a spring and record the extension of the spring. Ignoring the minus sign in Hookes law and dividing by the displacement, x, gives:
Using the elastic potential energy formula is a similarly straightforward process, but it doesnt lend itself as well to a simple experiment. However, if you know the elastic potential energy and the displacement, you can calculate it using:
In any case youll end up with a value with units of N/m.
Pressure Dependence Of Elastic Constants
In a strict application of Hooke’s law, the total energy U has no terms of higher order than cijij. In a real material, higher-order terms are present, thus causing the elastic constants to depend on pressure . Furthermore, when a crystal is under pressure the expansion of U in terms of small strains refers to a crystallographic unit cell that is smaller than that at zero pressure, which also affects cijdefined from derivatives of U.
The elastic constants are often determined from ultrasonic wave experiments. Then it is natural to speak of effective elastic constants, to be distinguished from the thermodynamic definition, as in eq. . As an example, we consider the pressure dependence of c11 determined from experiments as the ratio
S.M. Blinder, in, 2021
You May Like: Why There Are Different Branches Of Chemistry
Hookes Law And The Science Behind Springs
The humble spring is amazing in its simplicity and capability. Whether it is a compression spring design, torsion spring design or extension spring design, springs are engineered to serve a wide range of needs by providing stored energy.
In order to understand how springs work, one must consider the mechanics of the spring. Hookes Law is the principle of physics behind the elasticity, torsion, and force involved with springs.
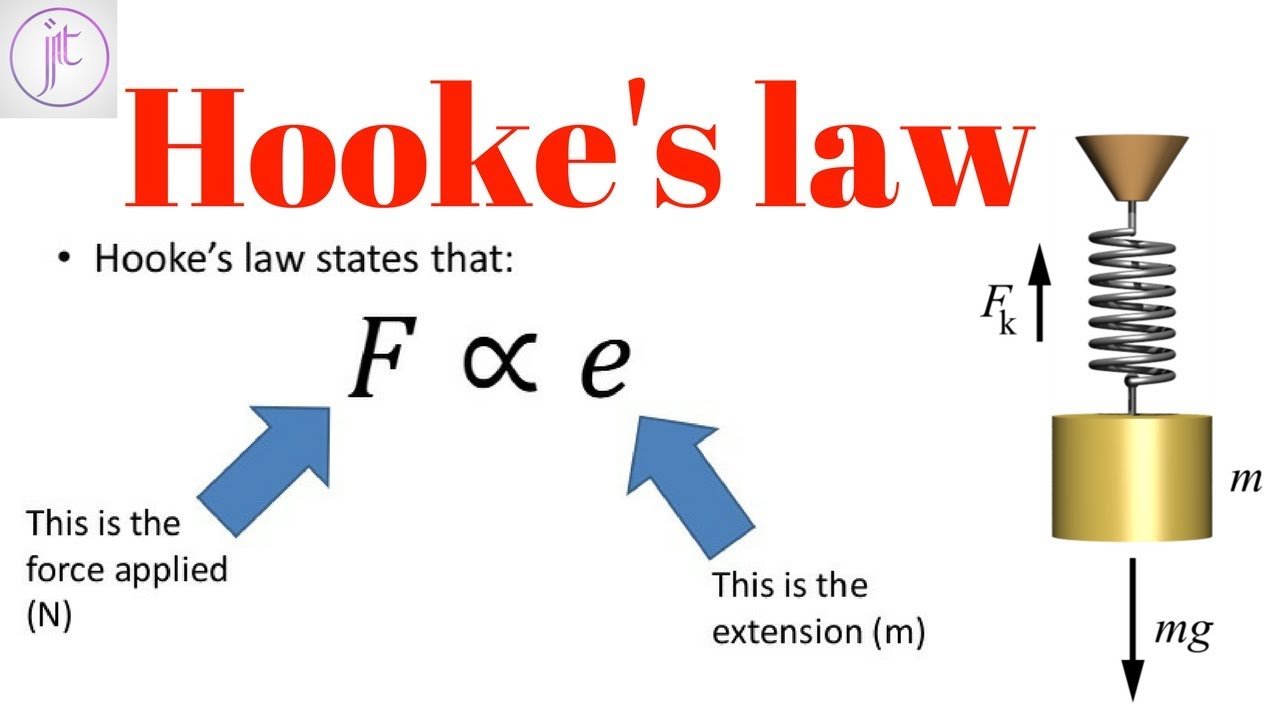
Hookes Law is named for 17th century British physicist, Robert Hooke. Hooke sought to demonstrate the relationship between the forces applied to a spring and its elasticity. Hookes Law states that the extension of a spring is proportional to the load that is applied to it. A variety of materials obey this law as long as the load does not exceed the materials elastic limit.
Hookes Law Equation
The length of a spring always changes by the same amount when it is pushed or pulled. In the case of a linear spring being pushed or pulled in one direction, the mathematical representation of Hookes Law is as follows:
F = kx
F being the amount of push or pull is on the spring
k being a constant, indicating the stiffness of the spring
x being the distance the spring was pushed or pulled
Elasticity and Restoring Force
The Limitations Of Hookes Law
Its important to stress again that Hookes law doesnt apply to every situation, and to use it effectively youll need to remember the limitations of the law. The spring constant, k, is the gradient of the straight-line portion of the graph of F vs. x in other words, force applied vs. displacement from the equilibrium position.
However, after the limit of proportionality for the material in question, the relationship is no longer a straight-line one, and Hookes law ceases to apply. Similarly, when a material reaches its elastic limit, it wont respond like a spring and will instead be permanently deformed.
Finally, Hookes law assumes an ideal spring. Part of this definition is that the response of the spring is linear, but its also assumed to be massless and frictionless.
These last two limitations are completely unrealistic, but they help you avoid complications resulting from the force of gravity acting on the spring itself and energy loss to friction. This means Hookes law will always be approximate rather than exact even within the limit of proportionality but the deviations usually dont cause a problem unless you need very precise answers.
Related Articles
Don’t Miss: Holt Mcdougal Geometry Workbook Answers
Anisotropy Of Axial Compression
Using Hooke’s law, a hydrostatic pressure, p, results in compressional strains 11, 12, 33. Since shears do not lead to any variations in volume, the uniaxial compressibilities are:
which is rotational invariant, whereas this does not apply for s11, s22 and s33.! For calculating the rotated linear compressibilities, S11 = {s11 + s12 + s13) etc., the rotated components s11, s12 and s13 are calculated by the transformation . For example we find S’11 with e‘1 = u11e1 + u12e2 + u13e3:
The components Sij form a second-rank tensor . For u11 = 1, etc. one again obtains the expressions of Equations to . One can use the ratio of the linear compressibility S’ and one third of the volume compressibility /3 as a measure of anisotropy, since this corresponds to an averaged linear compressibility, see Equ. . A percentage can also be given
In the calculational procedures one should note that u13 remains constant for rotations around e3.
A negative linear compressibility is also possible, as for tellurium. In this case, one axis expands under hydrostatic pressure but the total volume shrinks. Sometimes such behavior is also found in thermal expansion. The consequences of such an anomaly are a catastrophe for the polycrystalline system if a variation of temperature or external stress takes place.
as may be verified by substitution of the assumed form of the solution.
What Is Hookes Law
Hookes law states that for small displacement or deformations of an object, the displacement or deformation is directly proportional to the applied force or load. Hookes law can explain many mechanical properties and the strength of elastic materials. It enables us to understand the laws of elasticity in terms of force and torsion.
Historically, the law has been named after British physicist Robert Hooke. He established a relationship between force and displacement in 1660 and published it in 1678.
You May Like: Half Life Equations Chemistry
Is Hooke’s Law An Exact Law Of Physics Or An Approximation
On the other hand, Hooke’s law is an accurate approximation for most solid bodies, as long as the forces and deformations are small enough. The modern theory of elasticity generalizes Hooke’s law to say that the strain of an elastic object or material is proportional to the stress applied to it.
Beside this, what is Hooke’s Law in physics?
In terms of springs, this means understanding the laws of elasticity, torsion and force that come into play which together are known as Hooke’s Law. Hooke’s Law is a principle of physics that states that the that the force needed to extend or compress a spring by some distance is proportional to that distance.
Also, why is Hooke’s law important? Hooke’s Law, by Doodle Science, on youtube.comHookes law is important because it helps us understand how a stretchy object will behave when it is stretched or compacted. It relates to our everyday lives because without it, we would have a difficult time tweaking shocks on cars.
Similarly, how is Hooke’s Law derived?
Hooke’s Law states that the force needed to compress or extend a spring is directly proportional to the distance you stretch it. As an equation, Hooke’s Law can be represented as F = kx, where F is the force we apply, k is the spring constant, and x is the extension of the material .
What is the limitation of Hooke’s Law?
Applications Of Hookes Law
The applications of Hookes Law is as given below:
- Most commonly, in everyday life, Hookes Law is applied in springs because of their elasticity.
- They are used not only in the engineering field but also used in the field of medical science.
- It is used in breathing , skin, spring beds, diving boards and cars suspension systems.
- It is used as a fundamental principle behind the manometer, spring scale and balance wheel of the clock.
- It is also used as the foundation for seismology, acoustics and molecular mechanics.
Recommended Reading: Khan Academy Vapor Pressure
Example 3 Springs In Series
A mass is attached to two springs as shown. The spring on the right is compressed 20cm from its natural length. Calculate the force required to move the mass 10 cm to the left, at constant velocity.
Solution : In this situation, the spring on the left needs to be compressed, and because the spring on the right is compressed, it will provide some of the force needed to move the mass. We aren’t accelerating the mass, so we don’t have to exert a net force just to move it.
The force required to compress the spring on the left is
$$F_1 = – = 1.2 \ N$$
The force toward the left produced by the spring on the right is
$$F_2 = – = -0.8 \ N$$
Now the net force required to make the move is the sum of these two forces,
$$F_1 + F_2 = 1.2 \ N – 0.8 \ N = 0.4 \ N$$
Stress And Strain In Hookes Law

Stress and strain are essential properties of ductile materials. Consider any object that is subjected to an applied force resulting in deformation. Stress is a quantity that describes the magnitude of the applied force. It is defined as the force applied per area of the object. Strain is used to describing the deformation. It is defined as the ratio of change in length to the objects original length . Hookes law gives a relationship between stress and strain.
Stress = Modulus of Elasticity x Strain
Also Check: Geography Movement Definition
The Potential Energy Of A Spring
Springs store potential energy. When compressed or extended, a spring stores elastic potential energy that can be converted to kinetic energy and work.
The potential energy of a spring is
$$PE = \frac kx^2$$
If you know a little bit of calculus you can see in the section below how we derive that formula. The graph shows PE plotted vs. x for both negative and positive values of x . Study it for a bit. Notice that as the spring is further compressed or extended, the amount of potential energy it stores increases as the square of the distance.
Check out the animation below, too. The horizontal line marks the natural length of the spring/mass combination, the point at which PE = 0.
When the spring is compressed , the PE grows. It’s the same when the spring is extended.
When the spring changes direction at its most compressed point, it begins to exchange PE for kinetic energy , until it reaches its natural length, at which PE = 0 and KE is equal to the maximum PE gained in compression. It’s the same for extension. Follow the cycle a few times to make sure you get it.
Hookes Law: Stress And Strain Revisited
Newtonâs first law implies that an object oscillating back and forth is experiencing forces. Without force, the object would move in a straight line at a constant speed rather than oscillate. Consider, for example, plucking a plastic ruler to the left as shown in Figure 16.2. The deformation of the ruler creates a force in the opposite direction, known as a restoring force. Once released, the restoring force causes the ruler to move back toward its stable equilibrium position, where the net force on it is zero. However, by the time the ruler gets there, it gains momentum and continues to move to the right, producing the opposite deformation. It is then forced to the left, back through equilibrium, and the process is repeated until dissipative forces dampen the motion. These forces remove mechanical energy from the system, gradually reducing the motion until the ruler comes to rest.
The simplest oscillations occur when the restoring force is directly proportional to displacement. When stress and strain were covered in Newtonâs Third Law of Motion, the name was given to this relationship between force and displacement was Hookeâs law:
Don’t Miss: Glencoe Algebra 1 Chapter 4 Test Form 2a Answers
The Force Produced By Springs
Hooke’s law says that the force produced by a spring is proportional to the displacement of that spring:
F = -kx
where k is called the force constant or spring constant of the spring. Each spring has its own force constant.
The diagram defines all of the important dimensions and terms for a coil spring. For each mass hung on it , a spring has some natural length, at which it is neither compressed or extended . At that point, the upward force produced by the spring is exactly balancing the gravitational force on the mass and spring .
We define the coordinate x so that it is negative when the spring is compressed, zero at the natural length and positive when the spring is extended. The minus sign in F = -kx is there by convention we think of F as the restoring force. When the spring is compressed, a positive force is required to extend it, and when it is extended, a negative force is required to shorten it, or restore it to its natural length.
If the spring is strong or stiff, k will be large, and k will be small for a weak spring.
Hooke’s law is applicable not only to coil springs like the one shown here, but also to the bending of metal and some other materials, the stretching of wires like guitar strings, the stretching of rubber bands, and the stretching and compressing of chemical bonds.
The Hookes Law Formula
The spring constant is a key part of Hookes law, so to understand the constant, you first need to know what Hookes law is and what it says. The good news its a simple law, describing a linear relationship and having the form of a basic straight-line equation. The formula for Hookes law specifically relates the change in extension of the spring, x, to the restoring force, F, generated in it:
The extra term, k, is the spring constant. The value of this constant depends on the qualities of the specific spring, and this can be directly derived from the properties of the spring if needed. However, in many cases especially in introductory physics classes youll simply be given a value for the spring constant so you can go ahead and solve the problem at hand. Its also possible to directly calculate the spring constant using Hookes law, provided you know the extension and magnitude of the force.
Don’t Miss: Beth Thomas Now
Hooke’s Law For Continuous Media
The stresses and strains of the material inside a continuous elastic material are connected by a linear relationship that is mathematically similar to Hooke’s spring law, and is often referred to by that name.
However, the strain state in a solid medium around some point cannot be described by a single vector. The same parcel of material, no matter how small, can be compressed, stretched, and sheared at the same time, along different directions. Likewise, the stresses in that parcel can be at once pushing, pulling, and shearing.
In order to capture this complexity, the relevant state of the medium around a point must be represented by two-second-order tensors, the strain tensor and the stress tensor . The analogue of Hooke’s spring law for continuous media is then
- =\sum _^\sum _^c_\varepsilon _}
where i,j = 1,2,3.
All three tensors generally vary from point to point inside the medium, and may vary with time as well. The strain tensor merely specifies the displacement of the medium particles in the neighborhood of the point, while the stress tensor specifies the forces that neighboring parcels of the medium are exerting on each other. Therefore, they are independent of the composition and physical state of the material. The stiffness tensor c, on the other hand, is a property of the material, and often depends on physical state variables such as temperature, pressure, and microstructure.