What Is Fundamental Frequency Physics

Odd And Even Order Harmonics

The harmonics occurring at a frequency 3f, 5f, 7f, 9fâ¦etc are called the odd-order harmonics. The harmonics occurring at a frequency 2f, 4f, 6f, 8fâ¦etc are called the even-order harmonics.

In even order harmonics there is an equal number of positive and negative half-cycles so they cancel out and not significant in power system. While in case of odd harmonics there is a positive half cycle left in each order which does not cancel the negative half cycle, therefore it is significant in power system which add up and increase the neutral current and temperature rises.

The odd-order harmonics are mostly produced by the non-linear loads. The even-order harmonics are produced when the uneven current is drawn between the positive and negative half cycle of the fundamental frequency.

The electric arc furnaces, arc welders generate non-integer harmonics. Transformer magnetizing currents contain even order harmonic.

Example 1 Find The Length Of A Tube With A 128 Hz Fundamental

Strategy

The length L can be found from the relationship in f_n=n\frac}}\\, but we will first need to find the speed of sound vw.

Solution for Part 1

• the first overtone has n = 3
• the second overtone has n = 5
• the third overtone has n = 7
• the fourth overtone has n = 9

Enter the value for the fourth overtone into f_n=n\frac}}\\:

f_9=9\frac}}=9f_1=1.15\text\\

Discussion on Part 2

Whether this overtone occurs in a simple tube or a musical instrument depends on how it is stimulated to vibrate and the details of its shape. The trombone, for example, does not produce its fundamental frequency and only makes overtones.

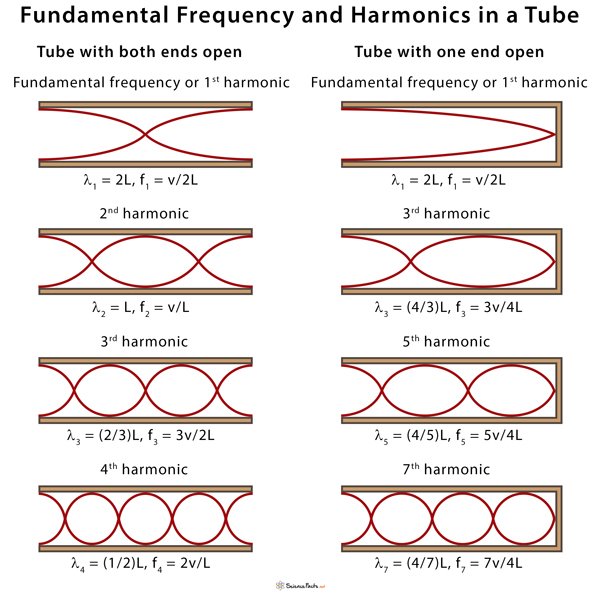
Another type of tube is one that is open at both ends. Examples are some organ pipes, flutes, and oboes. The resonances of tubes open at both ends can be analyzed in a very similar fashion to those for tubes closed at one end. The air columns in tubes open at both ends have maximum air displacements at both ends, as illustrated in Figure 11. Standing waves form as shown.

Figure 11. The resonant frequencies of a tube open at both ends are shown, including the fundamental and the first three overtones. In all cases the maximum air displacements occur at both ends of the tube, giving it different natural frequencies than a tube closed at one end.

f_n=n\frac}},n=1,2,3,\dots,\\

Fundamental Frequency And Harmonics

Suppose we hold a tuning fork near the end of a tube that is closed at the other end, as shown in Figure 14.21, Figure 14.22, and Figure 14.23. If the tuning fork has just the right frequency, the air column in the tube resonates loudly, but at most frequencies it vibrates very little. This means that the air column has only certain natural frequencies. The figures show how a resonance at the lowest of these natural frequencies is formed. A disturbance travels down the tube at the speed of sound and bounces off the closed end. If the tube is just the right length, the reflected sound arrives back at the tuning fork exactly half a cycle later, and it interferes constructively with the continuing sound produced by the tuning fork. The incoming and reflected sounds form a standing wave in the tube as shown.

L

The standing wave formed in the tube has its maximum air displacement at the open end, and no displacement at the closed end. Recall from the last chapter on waves that motion is unconstrained at the antinode, and halted at the node. The distance from a node to an antinode is one-fourth of a wavelength, and this equals the length of the tube therefore, λ

3 . There is a whole series of shorter-wavelength and higher-frequency sounds that resonate in the tube.

Also Check: Holt Mcdougal Geometry Workbook Answer Key

How Is Frequency Expressed

Frequency is usually expressed in the hertz unit, abbreviated Hz. One kilohertz is 1,000 Hz, and one megahertz is 1,000,000 Hz. In spectroscopy, another unit of frequency that is sometimes used is the wavenumber, the number of waves in a unit of distance.

frequency, in physics, the number of waves that pass a fixed point in unit time also, the number of cycles or vibrations undergone during one unit of time by a body in periodic motion. A body in periodic motion is said to have undergone one cycle or one vibration after passing through a series of events or positions and returning to its original state. See alsoangular velocity simple harmonic motion.

If the period, or time interval, required to complete one cycle or vibration is 1/2 second, the frequency is 2 per second if the period is 1/100 of an hour, the frequency is 100 per hour. In general, the frequency is the reciprocal of the period, or time interval i.e., frequency = 1/period = 1/. The frequency with which the Moon revolves around Earth is slightly more than 12 cycles per year. The frequency of the A string of a violin is 440 vibrations or cycles per second.

Fundamental Frequency And Harmonics In A String

In the case of a string, since its ends are fixed, it has zero displacements at the ends. These are known as nodes. The relationship between the wavelength and the length of the string is as follows: = L, where n is a whole number. In other words, there can be half a wave on the string , one wave , and one and a half waves . However, there can never be any other fraction of a wave because that would require not having a node at both ends.

Higher harmonics have nodes in other locations besides just at the ends. In between two nodes, there is a region where the vibrations are a maximum, and it is called antinode. The fundamental frequency has one antinode, and the 2nd harmonic has two antinodes.

A string has several frequencies at which it will naturally vibrate. The natural frequency at which the string vibrates depends upon its tension, linear density, and length of the string. Once the string density and tension are chosen, the speed is fixed, and the frequencies will depend on the wavelength, as shown in the following table. The harmonics are all multiples of the fundamental frequency.

Recommended Reading: Holt Geometry Chapter 7 Test Form A Answers

What Is Resonant Frequency

Any system that has at least a pair of complex conjugate poles has a natural frequency of oscillation. If the frequency of the system driving force coincides with the natural frequency of oscillation, the system resonates or resonant frequency and the system gives the maximum response.

Resonance is the phenomenon at which natural frequency coincides with the driving force and gives the maximum response. The resonant frequency is the frequency at which resonance happens. Resonance occurs in electrical systems when the system contains at least one inductor and one capacitor.

In this system, the phenomenon of cancellation of reactance when inductor and capacitor are in series or cancellation of susceptance when they are in parallel is termed as resonance. The circuit under resonance is purely resistive in nature and is termed as resonant circuit or tuned circuit.

Production Of Voice Tone

• In phonetics: Acoustic phonetics

  voiced soundis determined by its fundamental frequency, or rate of repetition of the cycles of air pressure. For a speaker with a bass voice, the fundamental frequency will probably be between 75 and 150 cycles per second. Cycles per second are also called hertz this is the standard term

• In speech: Vocal frequency

  vocal cord vibration is the fundamental tone of the voice, which determines its pitch. In physical terms, the frequency of vibration as the foremost vocal attribute corresponds to the number of air puffs per second, counted as cycles per second . This frequency is determined by both stable

Also Check: Algebra 1 August 2018 Regents Answers

Effects Of Positive Negative And Zero Sequence Harmonics

Due to a positive sequence harmonic the overheating of conductors, power lines and transformer takes place because of addition to the fundamental as itâs rotating in forward direction as the fundamental frequency.

Negative sequence harmonic circulates negative sequence current between the phases which causes the opposite phasor rotation and due to that the rotating magnetic field may be weakened and thus mechanical torque is reduced especially in the induction motors.

Zero sequence currents circulate between the phase and neutral which add up arithmetically in the common neutral wire and the neutral current becomes three times the phase current causing it to become less efficient and overheat.

Difference Between Fundamental Frequency And Natural Frequency

Fundamental Frequency vs Natural Frequency

Natural frequency and fundamental frequency are two wave related phenomena that are very important. These phenomena are of great significance in fields such as music, construction technologies, disaster prevention, acoustics and most of the natural system analysis. It is vital to have a clear understanding in these concepts in order to excel in such fields. In this article, we are going to discuss what fundamental frequency and natural frequency are, their definitions, applications, the phenomena connected to natural frequency and fundamental frequency, their similarities and finally the differences between natural frequency and fundamental frequency.

What is Natural Frequency?

What is Fundamental Frequency?

Don’t Miss: Linear Algebra What Is A Span

What Is A Harmonic In Physics

4.7/5harmonicharmonicsthoroughly answered

A harmonic of such a wave is a wave with a frequency that is a positive integer multiple of the frequency of the original wave, known as the fundamental frequency.

Furthermore, how do you find the harmonic of a wave? Wave overtones

Subsequently, question is, what is a harmonic in music?

Harmonics in music are notes which are produced in a special way. They are notes which are produced as part of the harmonic series. In physics, a harmonic is a wave which is added to the basic fundamental wave. This vibration makes the air vibrate and the sound waves travel to our ear so that we can hear it.

Why 3rd harmonics is dangerous?

rotates in the opposite direction of the fundamental frequency. Generally, positive sequence harmonics are undesirable because they are responsible for overheating of conductors, power lines and transformers due to the addition of the waveforms.

The Physics Of Sound In Tubes

This part of the Physics of sound is the basis of all wind instruments, from the piccolo to the organ. Basically the ideas are very simple but they can become complex for a specific musical instrument. For that reason we will confine ourselves to a general treatment of the production of a note from a uniform tube.

Read Also: Afda Mean Median Mode Range Practice

What Is The Relation Between The Fundamental Frequency And A Harmonic

I am currently busy with a physics report about determining the speed of sound in air. In order to do this, I was told to use a tube that can extend or shorten in order to find the different harmonics of the pipe for different frequencies. I am, however, struggling to understand how to execute the project correctly, what the purpose of the pipe is and how to use the data to get the speed of sound. I should also give the relation between the fundamental frequency and a harmonic and then use that relation to formulate an equation for determining the expected tube lengths that will resonate using a specific wavelength. The work is new to me and I am finding it very difficult to grasp, so if anyone can help me I would really appreciate it!

• $\begingroup$Hello Jeroen. This isnt the correct place to ask this question. Googling it will result in more help than asking it here.$\endgroup$ Superfast JellyfishFeb 5 ’20 at 15:05
• 1

Well, you kinda ask a lot of questions together here… I will do my best to help here, but I believe you should divide that into smaller chunks for your own convenience.

Starting with the question related to the title… As very well mmesser314 has pointed to in their comment you can find in Wikipedia that a harmonic is one that has a positive integer-multiple relation to the fundamental . In other words the frequency of ay harmonic will be

$$f_ = n \cdot f_ ~, n = 2, 3, 4, …$$

What Is Fundamental Frequency How Does It Make Sense

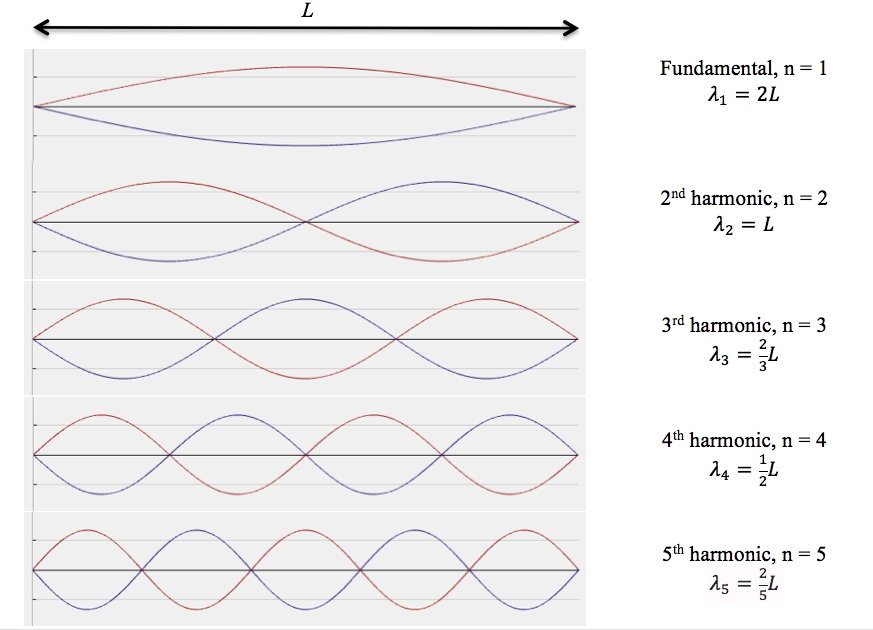
Im currently going through harmonics, and I do not at all understand the fundamental frequency. I understand that it is the simplest vibration of a string, but I don’t understand how can it have frequency at all if it is only half a wavelength. Isnt frequency how many cycles are completed per second, and isnt the fundamental frequency only half a cycle if it is half a wavelength? How can there be frequency of 162 cycles per second if one cycle doesnt even complete in the medium of the string? Is it measuring the frequency of the half wavelength as a full cycle? Is there frequency measured as a whole cycle from one half because it is a resultant wave of two waves making the half wavelength? If so, why do we have to multiply by two to get the wavelength of the cycle from the string length?

Isnt frequency how many cycles are completed per second, and isnt the fundamental frequency only half a cycle

When a string, fixed a both ends, vibrates in the fundamental mode, the perpendicular displacement $\phi_1$ of a point located at $x$ along the length of the string is given by

$$\phi_1 = A_1\phi_1 = A_1\cos\sin\left$$

Now, it is true that the spatial variation of the fundamental mode is a ‘half-cycle’ since the argument of the $\sin$ ranges from $0$ to $\pi$.

However, the fundamental frequency refers to the time dependent amplitude $A_1$. Note that $A_1$ executes $f_1$ cycles per second. Take a look at this animated gif of the fundamental mode and the first three harmonics:

Also Check: What Does Cyte Mean In Biology

Measurement Of The Velocity Of Sound

The velocity of sound in air may be found quite simply by using the resonance of a column of air in a tube. An open-ended tube is placed in a glass cylinder containing water, as shown in Figure 4, so that the water closes the bottom end of the tube. A tuning fork of known frequency is sounded over the upper end, the air in the tube vibrates and a note is heard. The length of the air column is adjusted by raising the tube out of the water until a point is found where resonance occurs and a loud note is produced. At this point the frequency of the tuning fork is equal to the resonant frequency of the tube.In its fundamental mode the wavelength A is four times the length of the air column , that is: l= 4LSince velocity = frequency x wavelength the velocity of sound may be found. For accurate determinations the following precautions should be taken: the temperature of the air should be taken, since the velocity of sound is temperature-dependent, and the end correction should be allowed for. This may be done by finding the resonance for the second harmonic with the same tuning fork.

Example problems

What Are The Effects Of Harmonics

Harmonic frequencies in the power grid cause power quality problems.

Harmonics in power systems result in increased heating in the equipment and conductors and create a pulsating torque in the motors.

Harmonics cause increasing operating temperature and the iron losses in the AC motors and transformers because hysteresis loss is proportional to the frequency and eddy current loss is proportional to the square of the frequency.

Harmonics create misfiring in the variable speed drives since harmonics are higher than fundamental frequencies and at a fundamental frequency the AC machines have a particular speed called a synchronous speed so at a higher frequency we got a speed difference i.e. slip difference.

In an induction motor crawling phenomenon occurs due to the space harmonics produced by the winding currents.

What Are Time Harmonics and Space Harmonics?

The harmonics which are generated by a source that varies non-sinusoidal in time which is always present in the input supply are known as time harmonics.

The harmonics which are a result of the non-sinusoidal distribution of the coils in the machine and slotting, due to that the air-gap mmf and flux are not sinusoidally distributed in space are known as space harmonics.

Don’t Miss: Eoc Fsa Practice Test Algebra 1 Calculator Portion

Frequency Time Period And Angular Frequency

As we know, many forms of energy like light and sound travel in waves. A wave is defined through various characteristics like frequency, amplitude and speed. In wave mechanics, any given wave enfolds parameters like frequency, time period, wavelength, amplitude etc. This article lets us understand and learn in detail about frequency, time period, and angular frequency.

Frequency definition states that it is the number of complete cycles of waves passing a point in unit time. The time period is the time taken by a complete cycle of the wave to pass a point. Angular frequency isangular displacement of any element of the wave per unit time.

Consider the graph shown below. It represents the displacement y of any element for a harmonic wave along a string moving in the positive x-direction with respect to time. Here, the element of the string moves up and down in simple harmonic motion.

The relation describing the displacement of the element with respect to time is given as:

y = a sin , here we have considered the inception of from x=0

y = -a

As we know, sinusoidal or harmonic motion is periodic in nature, i.e. the nature of the graph of an element of the wave repeats itself at a fixed duration. To mark the duration of periodicity following terms are introduced for sinusoidal waves.

Following is the table explaining other related concepts of waves: