Geometry Arc Length And Sector Area Worksheet Answer Key

Example: Find The Area Of A Sector A Circle K

Notice that this question is asking you to find the area of a sector of circle K, so you will have to use the Sector Area Formula to solve it!

Before you can use the Sector Area Formula, you will have to find the value of and the length of the radius of circle K.

You already know that the radius r is equal to 5. But what about ?

AKB and AKC are supplementary

In this example, is the measure of angle AKB, , but the question only tells you that AKC = 117 degrees.

Since AKB and AKC are supplementary, they have a sum of 180 degrees. You can find the measure of AKB as follows:

= AKB = 180 – 117 = 63 degrees.

So = 63 and r = 5

Now that you know the value of and r, you can substitute those values into the Sector Area Formula and solve as follows:

Replace with 63.

r^2 equals 5^2 = 25 in this example.

Simplify the numerator, then divide.

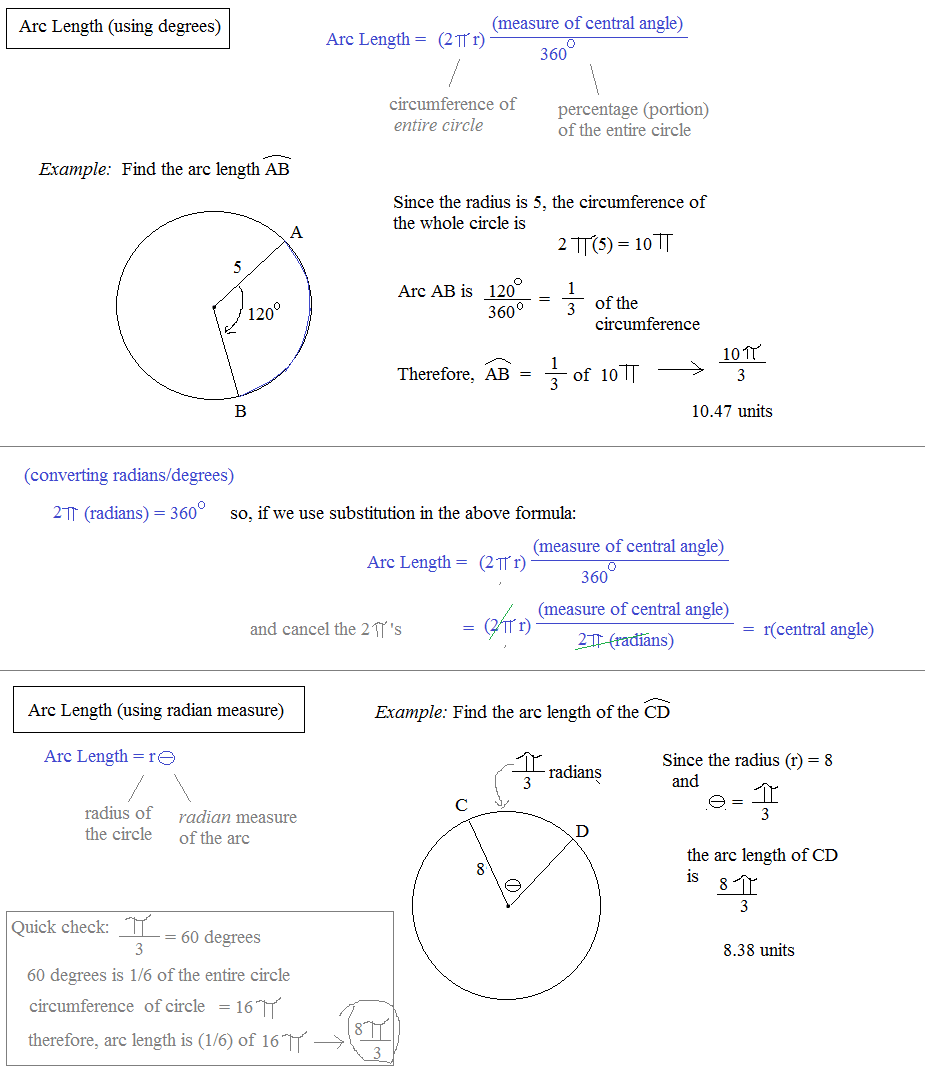
The Arc Lenth Formula:

What if you only want to find the length of a portion of the outside of a circle and not the entire circumference?

Whenever you want to find the length of an arc of a circle , you will use the arc length formula:

Where equals the measure of the central angle that intercepts the arc and r equals the length of the radius.

Worksheet On Arc Length And Area Of Sector

Question 1 :

Find the length of the arc that is bolded.

Question 2 :

In the diagram given below, if QRS is a central angle and mQRS = 81°, mSRT = 115°, and radius is 5 cm, then find the length of the arc QST.

Question 3 :

If mLMN = 19° and radius is 15 inches, then find the length of arc LN.

Question 4 :

Find the length of the arc highlighted in red color.

Question 5 :

Find the area of the sector that is outlined with the bold line.

Question 6 :

In circle C, if XCZ is a central angle and XYZ is an inscribed angle and mXYZ = 58° and radius is 10 inches. Find the area of sector XCZ.

Question 7 :

If QRS is a central angle and mQRS = 46°, mSRT = 80°, and diameter is 4 inches, then find the area of the shaded sector.

Recommended Reading: What Is Improvisation In Chemistry

Length Of The Arc Of Sector Formula

Similarly, the length of the arc of the sector with angle , is given by

Area of Sector with respect to Length of the Arc

If the length of the arc of the sector is given instead of the angle of the sector, there is a different way to calculate the area of the sector. Let the length of the arc be l. For the radius of a circle equal to r units, an arc of length r units will subtend 1 radian at the centre. Hence, it can be concluded that an arc of length l will subtend l/r, the angle at the centre. So, if l is the length of the arc, r is the radius of the circle and is the angle subtended at the centre, then

= l/r, where is in radians.

When the angle of the sector is 2, then the area of the sector is r2

When the angle is 1, the area of the sector = r2/2 = r2/2

So, when the angle is , area of the sector = × r2/2

A = ×

Some examples for better understanding are discussed here.

What Is Sector Of A Circle

The sector is basically a portion of a circle which could be defined based on these three points mentioned below:

• A circular sector is the portion of a disk enclosed by two radii and an arc.
• A sector divides the circle into two regions, namely Major and Minor Sector.
• The smaller area is known as the Minor Sector, whereas the region having a greater area is known as Major Sector.

Also Check: What Is Conscientiousness In Psychology

Geometry Arc Length And Sector Area Worksheet Answer Key

You can use the measure of the arc to fi nd its length . Symbols arc length of abs5} m 36 a 0 b 8} p2r arc length p a r r b arc length central angle} arc len 2 g th r of.

*Click “Save Image” to View FULL IMAGE

Convert each angle in radians to degrees. Arc length and area of a sector answer key sheet 1 t find the length of the arc and area of the shaded region. Applications of arc length and sectors a sector of a circle is a region of the circle bounded by a central angle and its intercepted arc.

Answer key arc length and area of a sector arc length of a sector = 1800 1800 = 10.47 cm score. A) 6.28 radians b) 1 radian c. 1 11 ft 315 60 5 ft 2 13 ft 270 61 3 ft 3 16 ft 3 .

Arc length an is a portion of the circumference of a circle. You can write a proportion to find arc length. Convert each angle in degrees to radians.

5) rs r s t q 6) major arc for 1 a b c 1 2 3 7) kql i j k l q 8) svt r s t u v q find the measure of the arc or central angle indicated. Arc length of a sector = 150 x 3.14 x 4 = 10.47 in # x ! 3) ml m l k 1 4) ml m l k q if an angle is given, name the arc it makes.

How do you find the length of a bow? Whether you want a homework, some cover work, or a lovely bit of extra practise, this is the place for you. And best of all they all come with answers.

You can use the measure of the arc to fi nd its length . An arc lengthis a portion of the circumference of a circle. solution :

Free Download

Get Geometry Arc Length And Sector Area Worksheet Answer Key

Arc length worksheet answer key. An arc lengthis a portion of the circumference of a circle. 1) 11 ft 315 ° 60.5 ft 2) 13 ft 270 ° 61.3 ft 3) 16 ft 3 2 75.4 ft 4) 13 in 6 6.8 in 5) r = 18 cm, = 60 ° 18.8 cm 6) r = 16 m, = 75 ° 20.9 m 7) r = 9 ft, = 7 4 49.5 ft 8) r = 14 ft, = 19 12 69.6 ft find the length of each arc. Arc length of a sector = 150 x 3.14 x 4 = 10.47 in # x !

Find the length of an arc that subtends a central angle of 45° in a circle of radius 10 m. 9) 8 cm 315 ° 14 cm 10) Sheet 1 area = = 20.94 crn2 4 cm 3.14) find the length of the arc and area of the shaded region.

Free Download

Don’t Miss: Why Teach Geography In Primary Schools

Arc Length Of The Sector Worksheets

Make your practice go with a swing using our free worksheets on finding the arc length of the sector. A brilliant bevy of printables, these exercises feature finding the arc length using the radius and central angle, calculating the length of the arc using the area of the sector, and finding the missing parameters. Our pdf worksheets on finding the arc length of the sector are available in customary and metric units.

These prepping resources are suitable for grade 8 and high school students.

CCSS: HSG.C

To calculate the arc length of the sector, students must divide the central angle by 360° and multiply that fraction by 2r . With practice, they’ll soon have this skill added to their repertoire!

What will be the arc length if the angle subtended by it is 25°? Since 25/360 = 5/72, children must multiply it by the circumference and round their answer up to two decimal places. They can take advantage of the answer key whenever required.

Remind 8th grade and high school learners that the area of a sector is times r² and that they must plug in the given values to find or r first and then use the obtained value to determine the arc length.

Example: Find The Length Of Arc Kl

Notice that this question is asking you to find the length of an arc, so you will have to use the Arc Length Formula to solve it!

Before you can use the Arc Length Formula, you will have to find the value of and the length of the radius of circle P.

You know that = 120 since it is given that angle KPL equals 120 degrees. And, since you know that diameter JL equals 24cm, that the radius equals 12 cm.

So = 120 and r = 12

= 120 and r = 12

Now that you know the value of and r, you can substitute those values into the Arc Length Formula and solve as follows:

Replace with 120.

1440/180 equals 8.

Also Check: What Does Ppp Mean In Geography

What Is The Formula For The Perimeter Of The Sector Of A Circle

The formula for the perimeter of the sector of a circle is where r is the radius of the circle and is the angle of the sector.

Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!

Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz

Arc Length And Sector Area

We can use our knowledge about the area of a circle to help us find the area of a sector. We know that the area of a circle is given by

but if a sector is only a part of a circle, we can just find the area of the part. For example, since a full rotation of a circle is \ radians, we know that any smaller angle would be a fractional part of \. For example,

That is, the angle \ radians is \ of a revolution. Lets generalize this:

Then a sector whose angle measure is \ is exactly \ of a circle.

Then the area of a sector is \ times the area of a circle. That is,

Example: Find the area of the sector

Solution: We just need to substitute the angle and the radius into our formula. But first we note that

Then \\left = \Large \frac}} = \Large \frac}i\)

Example: Find the area of the sector.

Solution: Again, we need to simply substitute our angle and radius into our formula. But we first need to convert \ into radians. We have \

Then the area of the sector is

Below you can some free math worksheets and practice.

Recommended Reading: What Is Purification In Chemistry

Area Arc Length And Perimeter Of Sectors Of Circles 60 Questions Across 5 Worksheets + Clipart

Subject: Mathematics

I have been teaching MATHEMATICS since 1990. I have regularly been commended on my classroom displays and the quality of my resources as I feel this enriches the student experience.As a self-taught graphic designer I now produce professional quality materials for our academy/academy chain across all departments including posters/banners and promotional materials. I am currently working on updating some older resources as well as developing new ones!

How To Use The Arc Length Formula And The Sector Area Formula:

Before you learn the arc length equation and the area of a sector equation, lets quickly review two very important circle properties: Circumference and Area

The circumference of a circle is the linear distance around the circle, or the length of the circle if it were opened up and turned into a straight line.

The area of a circle is the number of square units it takes to fill up the inside of the circle.

Note the circumference and area apply to the entire circle.

In the case of arc length and sector area, you will only be dealing with a portion of a circle.

Recommended Reading: How Does China’s Geography Influence Its Economy

Arc Length And Sector Area Guided Notes And Worksheets

The Sector Area Formula:

What if you only want to find the area of a portion of a circle and not the entire area?

Whenever you want to find area of a sector of a circle , you will use the sector area formula:

Where equals the measure of the central angle that intercepts the arc and r equals the length of the radius.

Now that you know the formulas and what they are used for, lets work through some example problems!

Recommended Reading: Differential Geometry And Machine Learning

Arc Length Worksheet Answer Key

Arc length worksheet answer key – Find the area of a sector a circle k The size of the pdf file is 41746 bytes. Arc length of a sector = 150 x 3.14 x 4 = 10.47 in # x !

X r 180 = a 180 b length of the arc ab s=? Arc length of ab 4.36 centimeters. Answer key length of arc sheet 1 find the arc length of each sector.

Find the length of the arc acb Find the arc length of the semicircle to the nearest foot. Round your answers to two decimal places.

Arc length worksheet answer key Round your answers to two decimal places. Find the length of the arc cd in the diagram shown below.

X r 180 = 180 1) length of the arc mn = 56.52 in area of a sector = 339.12 in! If an arc is given, name its central angle.