How To Find The Scale Factor Of A Dilation
To find the scale factor for a dilation, we find the center point of dilation and measure the distance from this center point to a point on the preimage and also the distance from the center point to a point on the image. The ratio of these distances gives us the scale factor, as Math Bits Notebook accurately states.
Using dilation scale factors, we can shrink or expand a figure to the size we desire, knowing that each angle is congruent, each segment is proportional, the slope of each segment is maintained, and the perimeter of the preimage and image have the same scale factor.
How to Find the Scale Factor
Next, youll learn how to perform the following operations:
What Is A Dilation In Geometry
In geometry, dilation is a specific type of transformation that changes the objects size while keeping its general shape the same.
Translations, reflections, and rotations are all rigid transformations because they maintain the objects size and shape. They change the location and/or orientation of the object.
Dilations are not rigid transformations because the size of the object will change.
Dilation With Scale Factor
Scale Factor is defined as the ratio of the size of the new image to the size of the old image. The center of dilation is a fixed point in the plane. Based on the scale factor and the center of dilation, the dilation transformation is defined.
- If the scale factor is more than 1, then the image stretches.
- If the scale factor is between 0 and 1, then the image shrinks.
- If the scale factor is 1, then the original image and the image produced are congruent.
Also Check: Whodunnit Algebra 2 Answer Key
How To Determine The Scale Factor
The scale factor can be determined by taking the ratio of the distance between a point on the image and the center of dilation to the distance between a corresponding point on the preimage and the center of dilation.
Example:
Find the scale factor if quadrilateral ABCD is dilated to produce quadrilateral EFGH for the center of dilation O below.
This means that the lengths of the sides of quadrilateral EFGH are the lengths of the corresponding sides of quadrilateral ABCD conversely ABCD is the size of EFGH.
Video Lesson & Examples
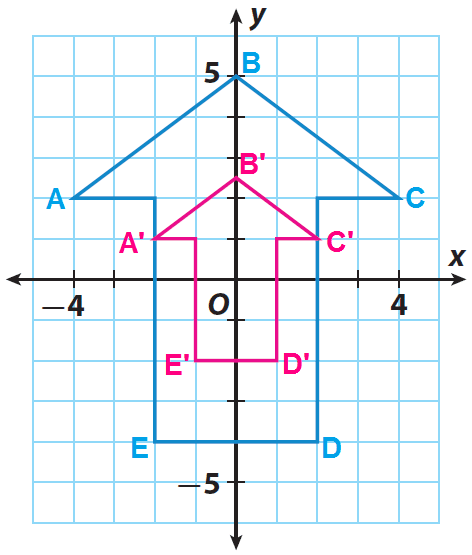
- Given the scale factor, determine if the dilation is a reduction or enlargement
- 00:09:48 Identify the dilation and determine its scale factor
- 00:13:53 Graph the dilation with the origin as the center point
- 00:20:02 Find the scale factor given select vertices from the preimage and image
- 00:28:27 Given a dilation solve for the indicated variables and find the ratio of perimeters
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Recommended Reading: What Is Oedipus Complex In Psychology
Summary Of A Dilation’s Properties
The following is a list of a few essential properties of dilations.
- The dilation of a line is a line.
- If the line does not pass through the center of dilation, the image line is parallel to the preimage.
- If the line passes through the center of dilation, the image line and the preimage line are the same.
Where Does The Image Land
When the scale factor is between 0 and 1, the image is between the preimage and the center of dilation. When the scale factor is greater than 1, the preimage is between the image and the center of dilation.
Below is a diagram showing a composite of the two dilations of triangle ABC.
Triangle DEF lies between the preimage of triangle ABC and point O, the center of dilation, since the scale factor was less than 1. Triangle ABC lies between the dilated triangle GHI and the center of dilation since the scale factor was greater than 1. Also, all three triangles are similar.
The closer the scale factor is to 1, the closer the image of the dilated triangle is to the preimage. Triangle ABC is dilated by a scale factor of to produce triangle DEF:
Read Also: Year 10 Coordinate Geometry Test
Dilation Meaning In Math
Dilation is a transformation, which is used to resize the object. Dilation is used to make the objects larger or smaller. This transformation produces an image that is the same as the original shape. But there is a difference in the size of the shape. A dilation should either stretch or shrink the original shape. This transformation is expressed by the term scale factor.
- If a dilation creates a larger image, then it is known as enlargement.
- If a dilation creates a smaller image, then it is known as reduction.
In the above figure, we can see, the triangle ACB is transformed into a bigger triangle, i.e., ABC after the dilation process. Hence, it is the case of enlargement of the size of an object or shape.
How To Do Dilations In Geometry
When dilating a figure in geometry, begin by finding the key points of the object. These will be endpoints, vertices, and centers.
Then, find the fixed point. If the point is not a key point of the object, draw a line from the key points to the fixed point.
Next, multiply the length of each line segment in the object by the factor of dilation.
Draw the new figure in the coordinate so that the fixed point is in the same spot.
Don’t Miss: What Is Space In Human Geography
Scale Factor Between 0 And 1
If the scale factor is between 0 and 1, the preimage decreases in size.
The preimage of triangle ABC is dilated with respect to point O by a scale factor of to produce the image of triangle DEF. The length of each side of the preimage is multiplied by to produce each corresponding side of the image. Also, points on triangle DEF are the distance from O relative to their corresponding points on triangle ABC.
How To Construct The Dilation Of An Object
You May Like: What Is Density In Physics
How To Perform Dilation
Now that we know about the process and types of dilation, we then discuss how we can perform dilations. For any given geometric figure in a coordinate plane, a dilation of scaling factor k can be done by scaling the coordinates of its vertices by the value of k:
A’ = A
In the above equation, the coordinates of the scaled vertex A is obtained by multiplying both horizontal and vertical coordinates of the original vertex A by the scaling factor k.
We consider an example to guide us in learning how to perform dilation. In the figure below, we have a triangle ABC whose vertices are shown:
Suppose we have the center of dilation at the origin O, and the scaling factor is k=2. We wish to find the coordinates of the scaled triangle ABC using dilation.
We first find the coordinates of the scaled vertices A, B, and C by multiplying the scaling factor by the original coordinates:
A’ = A
Hence, we have the coordinates of the scaled triangle ABC:
Plotting the points in the coordinate plane, we can see that the scaled triangle is twice the size of the original triangle:
An alternative method we can use is through measuring the distances between the vertices and the center of dilation. If we take the distance between the vertices of the triangle and the origin, we have the lengths of the line segments formed by the center of dilation and each vertex as:
OA=1
OB= 2
OC=1
OA=kOA
Substituting the given distances, we have:
OA = 21 = 2
OB = 22 = 22
OC = 21 = 2
How Do We Know That Two Shapes Are Similar
For two shapes to be similar, we have the following conditions:
For example, two triangles ABC and XYZ are said to be similar if the following conditions hold:
- The lengths of their sides are proportional to each other
$\frac = \frac = \frac$
- The measures of their corresponding angles are equal
AX
CZ
Don’t Miss: How To Study Chemistry On Your Own
Investigating Dilations In The Real World
On the image you can see a photograph taken in Tennoji Park in Osaka, Japan.
- Move the sliders to move the orange figure on the left.
- Suppose you were to draw this image, standing in a different position than this image’s photographer. How could you draw the image so that the two figures’ heights always appear to be the same?
info
Center Of Dilation Is Not The Origin
Let be the coordinates of the center of dilation. Given that a is a scale factor that is greater than zero, the point is dilated to a point , as shown below.
To determine the coordinates of the dilated point, add the horizontal and vertical distances to the x- and y-coordinates of the center of dilation:
= , d + a)
Example:
Dilate triangle ABC given vertices A , B , and C , scale factor of 2, and a center of dilation of O .
Using the formula from above, we can find the coordinates for the new vertices D, E, and F and graph them as follows:
| D = |
You May Like: What Is Secondary Succession In Biology
Scale Factor Greater Than 1
If the scale factor is greater than 1, the preimage increases in size.
Triangle ABC is dilated with respect to point O by a scale factor of to produce triangle GHI. The length of each side of the preimage is multiplied by to produce each corresponding side of the image. Also, points on triangle GHI are the distance from O relative to their corresponding points on triangle ABC.
How Do We Use The Distance Formula
We first need two points whose coordinates are known. Then, we substitute these x and y coordinates to the formula. We can use designate either point as the first point or the second point, as long as the substitution remains consistent in the formula.
After evaluating the expression inside the radical, we can then obtain the distance between those said points.
Recommended Reading: College Algebra Chapter 1 Study Guide
How Do We Find The Coordinates Of A Point
If the coordinates of a point are not given, and its plot on the coordinate plane is shown instead, we can look at the horizontal and vertical distance the point has from the origin:
Suppose we have the point A and we want to know its coordinates . To do this, we first measure how many steps the point is from the x-axis:
From the origin , we measure three steps to the positive direction of the x-axis. Hence, we say that the x-coordinate of point A is 3:
Next, we then measure how many steps the point is from the y-axis:
From the point , we measure two steps to the positive direction of the y-axis. Hence, we say that the y-coordinate of point A is 2.
Therefore, we conclude that the coordinates of point A is given by:
How To Find The Scale Factor Of A Dilated Figure
The scale factor can either increase or decrease the size of an object. The basic formula to find the scale factor of a dilated figure is: Scale factor = Dimension of the new shape ÷ Dimension of the original shape. For example, if a square is dilated and the side of the smaller square is 4 units and the side of the dilated square is 12 units, then, in this case, the scale factor will be: 12 ÷ 4 = 3.
You May Like: What Is Phase In Chemistry
Properties Of A Dilation
The following applet shows the images of points on a straight line. There are two modes in the applet, Setup
â complete the first to reach the next.
- In setup mode, set the scale factor, move the line, and slide the center of dilation as you please.
- Once done with the setup, move the point on the line to a different position. Then, mark the image point on the board. Mark multiple points.
- What do you notice about the image points?
info
What Is A Dilation
A dilation is a transformation that enlarges or reduces a figure in size. This means that the preimage and image are similar and are either reduced or enlarged using a scale factor.
As seen in the graphics below. A reduction is a dilation that creates a smaller image, and an enlargement is a dilation that creates a larger image.
Dilation Reduction
Dilation Enlargement
Also Check: Does Nicole Kidman Have Biological Children
What Is The Rule For Dilations
The transformation of geometrical shapes depends on the dilation scale factor. The scale factor follows three rules to transform any shape. These rules are:
- When k is unchanged, the size of the image will unchanged.
- When k is greater than 1, the image size will stretch outside.
- When k is less than 1, the image will shrink from inside.
What Is Dilation
Dilation is a transformation that resizes a geometrical shape while maintaining its orientation. We can think of dilation as enlarging or shrinking an object, like inflating a balloon, zooming in and out on a digital photo, or comparing two printouts of different sizes.
In this case, we can also say that dilation produces a similar shape as the original, since the proportion of the dimensions, as well as their angle measures, are preserved:
Also Check: Linear Algebra First Year University