Chapter 2linear Combinations Span And Basis Vectors
Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in a larger dose, would be insanity.
\qquad Angus K. Rodgers
In the last chapter, along with the ideas of vector addition and scalar multiplication, I described vector coordinates, where theres this back-and-forth between pairs of numbers and two-dimensional vectors.
Now I imagine that vector coordinates were already familiar to many of you, but theres another interesting way to think about these coordinates, which is central to linear algebra. When you have a pair of numbers meant to describe a vector, like , I want you to think of each coordinate as a scalar, meaning think about how each one stretches or squishes vectors.
xy-coordinate system, there are two special vectors. The one pointing to the right with length 1 1, commonly called i hat i ^ \hat i i^ or the unit vector in the x-direction. The other one is pointing straight up with length 1 1, commonly called j hat j ^ \hat j j^ or the unit vector in the y-direction. Now, think of the x-coordinate as a scalar that scales i i^, stretching it by a factor of 3 3, and the y-coordinate as a scalar that scales j j^, flipping it and stretching it by a factor of 2
Proof That Every Vector Space Has A Basis
Let V be any vector space over some field F. Let X be the set of all linearly independent subsets of V.
The set X is nonempty since the empty set is an independent subset of V, and it is partially ordered by inclusion, which is denoted, as usual, by â.
Let Y be a subset of X that is totally ordered by â, and let LY be the union of all the elements of Y .
Since is totally ordered, every finite subset of LY is a subset of an element of Y, which is a linearly independent subset of V, and hence LY is linearly independent. Thus LY is an element of X. Therefore, LY is an upper bound for Y in : it is an element of X, that contains every element of Y.
As X is nonempty, and every totally ordered subset of has an upper bound in X, Zorn’s lemma asserts that X has a maximal element. In other words, there exists some element Lmax of X satisfying the condition that whenever Lmax â L for some element L of X, then L = Lmax.
It remains to prove that Lmax is a basis of V. Since Lmax belongs to X, we already know that Lmax is a linearly independent subset of V.
If there were some vector w of V that is not in the span of Lmax, then w would not be an element of Lmax either. Let Lw = Lmax ⪠. This set is an element of X, that is, it is a linearly independent subset of V . As Lmax â Lw, and Lmax â Lw , this contradicts the maximality of Lmax. Thus this shows that Lmax spans V.
Basis Of A Vector Space
Let \ be a vector space.A minimal set of vectors in \ that spans \ is called abasis for \.
Equivalently, a basis for \ is a set of vectors that
is linearly independent
As a result, to check if a set of vectors form a basis for a vector space,one needs to check that it is linearly independent and that it spansthe vector space. If at least one of these conditions fail to hold,then it is not a basis.
You May Like: What Is Edge In Geometry
What Is The Intuitive Meaning Of The Basis Of A Vector Space And The Span
The formal definition of basis is:
A basis of a vector space $V$ is defined as a subset $v_1, v_2, . . . , v_n$ of vectors in that are linearly independent and span vector space $V$.
The definition of spanning is:
A set of vectors spans a space if their linear combinations fill the space.
But what is the intuitive meaning of this, and the idea of a vector span? All I know how to do is the process of solving by putting a matrix into reduced row-echelon form.
Take, for example $V = \mathbb R ^2$, the $x$-$y$ plane. Write the vectors as coordinates, like $$.
Such a coordinate could be written as a sum of its $x$ component and $y$ component: $$ = + $$and it could be decomposed even further and written in terms of a “unit” x vector and a “unit” y vector:$$ = 3\cdot + 4\cdot.$$The pair $\$ of vectors span $\mathbb R^2$ because ANY vector can be decomposed this way:$$ = a + b$$or equivalently, the expressions of the form $a + b$ fill the space $\mathbb R^2$.
It turns out the $$ and $$ are not the only vectors for which this is true. For example if we take $$ and $$ we can still write any vector:
$$ = 3\cdot + 1\cdot$$and more generally$$ = a \cdot + \cdot.$$
This fact is intimately linked to the matrix $$\left$$ whose row space and column space are both two dimensional.
I would keep going, but your question is general enough that I could write down an entire linear algebra course. Hopefully this gets you started.
Lecture : Independence Basis And Dimension

arrow_backlibrary_books
What does it mean for vectors to be independent? How does the idea of independence help us describe subspaces like the nullspace? A basis is a set of vectors, as few as possible, whose combinations produce all vectors in the space. The number of basis vectors for a space equals the dimension of that space.
These video lectures of Professor Gilbert Strang teaching 18.06 were recorded in Fall 1999 and do not correspond precisely to the current edition of the textbook. However, this book is still the best reference for more information on the topics covered in each lecture.
Strang, Gilbert. Introduction to Linear Algebra. 5th ed. Wellesley-Cambridge Press, 2016. ISBN: 9780980232776.
Instructor/speaker: Prof. Gilbert Strang
Don’t Miss: How To Do Friction Problems In Physics
Basis Of Span With Functions
I’m not sure how to solve the following problem:
Determine a basis and the dimension of $\langle e^, t^2, t \rangle$
When finding the basis of a span of vectors, I create a matrix and reduce the matrix to row-echolon form. If there is a row without a pivot, I know that the corresponding vector is not part of the basis. Since this is a span of functions instead of vectors, I’m not sure how to solve this.
From what I have found on the exchange here, I know that, in order for this span to be a basis, it should satisfy the following:$$a\cdot e^+b\cdot t^2+c\cdot t = 0 \quad\text\quad a = b = c = 0$$
But step $2$ means that $b$ and $c$ can basically be any number right?However, according to the answer sheet the given span should be a basis. What am I missing?
And is there a way I can solve questions like these with a matrix as well?
You can solve it with matrices, sort of.
To check linear independence of a set $\$ of twice differentiable functions on $\mathbb$, you can calculate the Wronskian, the determinant defined as:$$W = \begin f_1 & f_2 & f_3 \\f_1′ & f_2′ & f_3’\\f_1” & f_2” & f_3”\end$$
Notice that if your functions satisfy $\alpha f_1 + \beta f_2 + \gamma f_3 = 0$ on $\mathbb$, then linearity of the derivative also implies $$\alpha f_1′ + \beta f_2′ + \gamma f_3′ = 0$$$$\alpha f_1” + \beta f_2” + \gamma f_3” = 0$$
In your case, we have:
Dimension Of A Vector Space
Let \ be a vector space not of infinite dimension.An important result in linear algebra is the following:
Every basis for \ has the same number of vectors.
dimension
It can be shown that every set of linearly independent vectorsin \ has size at most \\).For example, a set of four vectors in \cannot be a linearly independent set.
You May Like: How To Solve Geometry Problems Step By Step
Understanding The Difference Between Span And Basis
I’ve been reading a bit around MSE and I’ve stumbled upon some similar questions as mine. However, most of them do not have a concrete explanation to what I’m looking for.
I understand that the Span of a Vector Space $V$ is the linear combination of all the vectors in $V$.
I also understand that the Basis of a Vector Space V is a set of vectors $, v_, …, v_}$ which is linearly independent and whose span is all of $V$.
Now, from my understanding the basis is a combination of vectors which are linearly independent, for example, $$ and $$.
But why?
The other question I have is, what do they mean by “whose span is all of $V$” ?
On a final note, I would really appreciate a good definition of Span and Basis along with a concrete example of each which will really help to reinforce my understanding.
Thanks.
- 2$\begingroup$Here is a lecture from Gilbert Strang about Span and Basis. His explanation is very good, so posting the video here instead of instead of answering it again. All the sessions around Linear Algebra can be found here.$\endgroup$
Span is usually used for a set of vectors. The span of a set of vectors is the set of all linear combinations of these vectors.
So the span of $\1\\0\end, \begin0\\1\end\}$ would be the set of all linear combinations of them, which is $\mathbb^2$. The span of $\2\\0\end, \begin1\\0\end, \begin0\\1\end\}$ is also $\mathbb^2$, although we don’t need $\begin2\\0\end$ to be so.
Subsection271basis Of A Subspace
As we discussed in Section 2.6, a subspace is the same as a span, except we do not have a set of spanning vectors in mind. There are infinitely many choices of spanning sets for a nonzero subspace to avoid reduncancy, usually it is most convenient to choose a spanning set with the minimal number of vectors in it. This is the idea behind the notion of a basis.
Definition
is a set of vectors {
Recall that a set of vectors is linearly independent if and only if, when you remove any vector from the set, the span shrinks . In other words, if { is a basis of a subspace V then no proper subset of { V : it is a minimal spanning set. Any subspace admits a basis by this theorem in Section 2.6.
A nonzero subspace has infinitely many different bases, but they all contain the same number of vectors.
We leave it as an exercise to prove that any two bases have the same number of vectors one might want to wait until after learning the invertible matrix theorem in Section 3.5.
Definition
The number of vectors in any basis of V is called the dimension of V
The previous example implies that any basis for R
Recommended Reading: Honors Algebra 2 Linear Function Word Problems Answers
To Know Everything About A Vectorspace Just Meet Mr Basis
Suppose $V$ is a vectorspace of uncountable number of elements over the field $F$ and suppose $V$ is of finite dimensional space. Then any element $\bf$ of $V$ can be represented as linear combination of all elements of $V$.
$=\sum_\in V}\alpha_u \textbf}$, where $\alpha_u\in F$.
This above representation is not unique! and interestingly, the element $\bf$ is represented by uncountable number of elements of $V$.
For example, consider $V=\mathbb^2$ over the field $F=\mathbb$ and $B=\_1,\bf_2\}$, where $\bf_1=,\bf_2=$.Any element $\displaystyle == x \textbf_1+y\textbf_2+\sum_\in V-\}\alpha_u \textbf}$, where $\alpha_u=0 \in F=\mathbb$, for all $\bf$.
–To remember all details of the uncountable set $\mathbb^2$, it is simple to remember a basis $B$!!
@Answer to Qn 1 and Qn 2: Linear independency of the basis will take care of it.
My answer is in the context of $\mathbb^n$, and I will work directly with the usual definitions of basis, span, and linear independence. I believe doing it this way is helpful because this is the perspective of many students taking linear algebra : working in Euclidean space, and wanting to understand how the intuition relates directly to the abstract definitions.
Choosing Different Basis Vectors
For example, take some vector pointing up and to the right, along with a vector pointing down and to the right.
In the above figure, \overrightarrow}=\begin1\\ 2\end v \overrightarrow}=\begin3\\ -1\end w
What values of the scalars satisfy the following equation? \alpha\vec}+\beta\vec}=5\hat i -\frac12\hat j v
We have a new pair of basis vectors v \overrightarrow} w. Take a moment to think about all the different vectors you can get by choosing two scalars, using each to scale one of the vectors, then adding them. Which two-dimensional vectors can you reach by altering your choice of scalars?
The answer is that you can describe every possible two-dimensional vector this way, and I think its a good puzzle to contemplate why. A new pair of basis vectors like this still gives you a way to go back and forth between pairs of numbers and two-dimensional vectors, but the association is definitely different from the version you get using the standard basis of i \hat j j^.
Ill go into much more detail on this point in a later chapter, describing the relationship between different coordinate systems, but for now I just want you to appreciate that any way to describe vectors numerically depends on your choice of basis vectors.
Read Also: How To Solve For Time In Physics
Subsection272computing A Basis For A Subspace
Now we show how to find bases for the column space of a matrix and the null space of a matrix. In order to find a basis for a given subspace, it is usually best to rewrite the subspace as a column space or a null space first: see this important note in Section 2.6.
A basis for the column space
First we show how to compute a basis for the column space of a matrix.
Theorem
The pivot columns of a matrix A
This is a restatement of a theorem in Section 2.5.
The above theorem is referring to the pivot columns in the original matrix, not its reduced row echelon form. Indeed, a matrix and its reduced row echelon form generally have different column spaces. For example, in the matrix A
the pivot columns are the first two columns, so a basis for Col
The first two columns of the reduced row echelon form certainly span a different subspace, as
contains vectors whose last coordinate is nonzero.
Corollary
is the number of pivots of A .
A basis of a span
Computing a basis for a span is the same as computing a basis for a column space. Indeed, the span of finitely many vectors v is the column space of a matrix, namely, the matrix A
A basis for the null space
In order to compute a basis for the null space of a matrix, one has to find the parametric vector form of the solutions of the homogeneous equation Ax 0.
Theorem
The vectors attached to the free variables in the parametric vector form of the solution set of Ax ) .
A basis for a general subspace
Difference Between Span And Basis
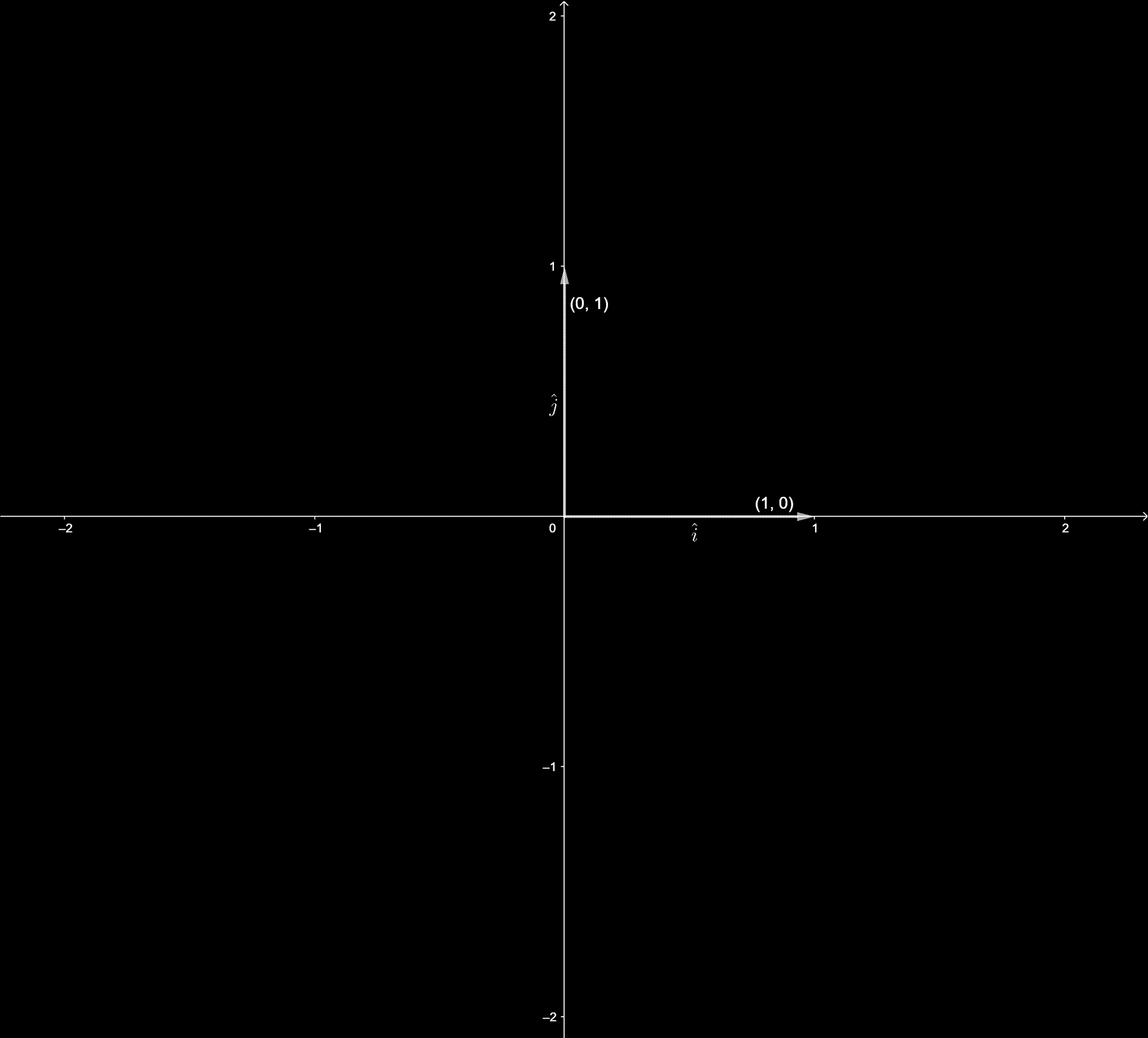
What is the difference between the span of the image of a matrix and the basis for the span of the image of a matrix? Are these the same thing?
A spanning set for a space is a set of vectors from which you can make every vector in the space by using addition and scalar multiplication .
For example in $\mathbb^2$ the three vectors $,$ and $$ form a spanning set. I can make the vector $$ by doing $x+y$.
A basis for a space is a spanning set with the extra property that the vectors are linearly independent. This essentially means that you can’t make one of the vectors in the spanning set out of the others. In other words a basis is a kind of most efficient spanning set, there are no vectors in our spanning set that weren’t needed.
For example in $\mathbb^2$ our spanning set above is not a basis since $$ is redundant in the span, we could already make it with $,$. However the set $\$ is a basis since we cannot discard any more vectors and still span the plane.
Recommended Reading: Geometry Angle Pairs Worksheet Answers
How To Understand Basis
When teaching linear algebra, the concept of a basis is often overlooked. My tutoring students could understand linear independence and span, but they saw the basis how you might see a UFO: confusing and foreign. And thats not good, because the basis acts as a starting point for much of linear algebra.
We always need a starting point, a foundation to build everything else from. Words cannot