Measures Of Central Tendency Example
Let us understand the concept of the measures of central tendency using an example. The monthly salary of an employee for the 5 months is given in the table below,
| Month | |
| May | $100 |
Suppose, we want to express the salary of the employee using a single value and not 5 different values for 5 months. This value that can be used to represent the data for salaries for 5 months here can be referred to as the measure of central tendency. The three possible ways to find the central measure of the tendency for the above data are,
Mean: The mean salary of the given salary can be used as on of the measures of central tendency, i.e., x = /5 = $102.
Mode: If we use the most frequently occurring value to represent the above data, i.e., $105, the measure of central tendency would be mode.
Median: If we use the central value, i.e., $105 for the ordered set of salaries, given as, $95, $100, $105, $015, $105, then the measure of central tendency here would be median.
We can use the following table for reference to check the best measure of central tendency suitable for a particular type of variable:
| Type of Variable | |
| Interval/Ratio | Median |
Let us study the following measures of central tendency, their formulas, usage, and types in detail below.
What Is A Symmetric Distribution
Symmetric distribution is also called Normal distribution or Zero-skewed distribution.
In a Symmetric distribution, the left side of the distribution mirrors the right side, i.e. the distribution of data shows zero skewness. Have a look at the figure given below:
As you can see, in a symmetric distribution, the mean, median, and mode coincide with each other. That is, Mean = Median = Mode
Mean As A Measure Of Central Tendency
The mean often called the average is most likely one of the measures of central tendency that you are most familiar with. It is also known as average. Mean is simply the sum of all the components in a group or collection, divided by the number of components.
We generally denote the mean of a given data-set by x, pronounced x bar. The formula to calculate the mean for ungrouped data to represent it as the measure is given as,
For a set of observations: Mean = Sum of the terms/Number of terms
For a set of grouped data: Mean, x = fx/fwhere,
- x = the mean value of the set of given data.
- f = frequency of each class
- x = mid-interval value of each class
Example: The weights of 8 boys in kilograms: 45, 39, 53, 45, 43, 48, 50, 45. Find the mean weight for the given set of data.
Therefore, the mean weight of the group:
Mean = Sum of the weights/Number of boys= /8= 368/8
Thus, the mean weight of the group is 46 kilograms.
Read Also: What Is L In Physics
Descriptive Statistics: Measures Of Central Tendency
Obtaining descriptive statistics often involves using a few numbers to summarise data. There are two aspects involved in using descriptive statistics:
- determining where the centre of the distribution is located and
- determining how much the scores in the distribution vary from one another .
Mean, mode and median are measures of central tendency and provide a single representative or typical value in a distribution. This section covers the measures of central tendency employed in descriptive statistics, how to compute them, and the main differences between them.
Lets Learn About Mean
For a given set of observations, the arithmetic mean may be defined as the sum of all the observations divided by the number of observations. This can be explained easily by solving an example. Let us assume that there are five observations: 10, 20, 30, 40, and 50.
According to the formula, the sum of total observations is 150 and the number of observations is 5. Then we put these observations in the formula and get = 150 / 5 = 30. Thus, the mean of the set of observations is 30. Similarly, in the case of grouped data, the formula for mean is, x = fX/N.
Where,
X = observations of the set of given data.
f = frequency of the individual data
N = sum of frequencies
Read Also: Math Caching Algebra 1 Answers
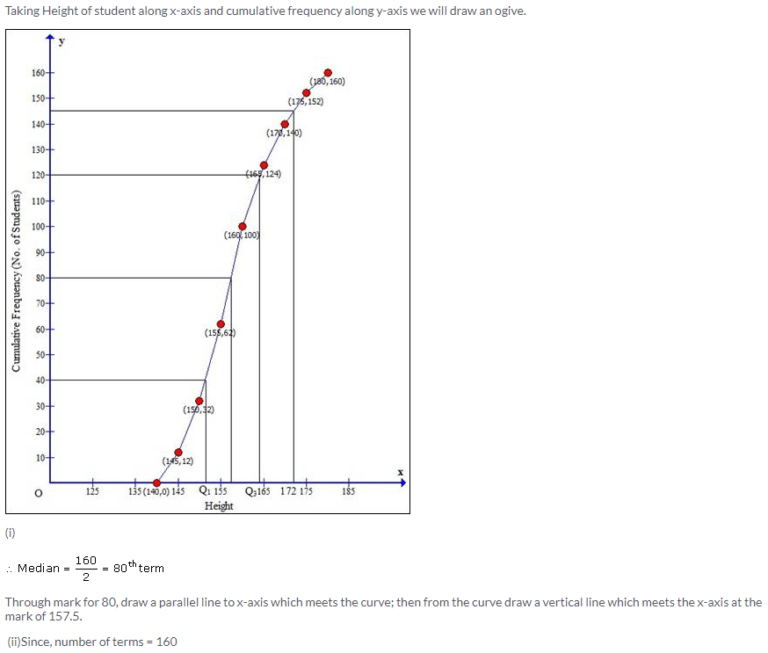
Using Median To Plan Capacity
In the data center, means and medians are often tracked over time to spot trends, which inform capacity planning or power cost predictions.The statistical median is the middle number in a sequence of numbers. To find the median, organize each number in order by size the number in the middle is the median. For the five servers in the rack, arrange the power consumption figures from lowest to highest: 90 W, 98 W, 100 W, 102 W and 105 W. The median power consumption of the rack is 100 W. If there is an even set of numbers, average the two middle numbers. For example, if the rack had a sixth server that used 110 W, the new number set would be 90 W, 98 W, 100 W, 102 W, 105 W and 110 W. Find the median by averaging the two middle numbers: /2 = 101 W.
What Is Mean Value
The mean value is the average value that falls between the maximum and minimum values in the data set, but it is not a number in the data set. A formula for Mean is as follows,
There is another method of calculating mean that is not widely used. This method is known as the Assumed Mean Method. In this case, a random value from the data set is chosen and assumed to be the mean. The deviation of the data points from this value is then computed. As a result, the mean is given by:
Mean = Assumed Mean +
Read More:
Read Also: When To Use Distribution In Math
The Greeks Estimation Of Sailors
Referring again to an account from the Greeks, who this time were attempting to count the number of sailors in their fleet. This was done by taking the known largest and smallest ship sailor numbers before finding the average and multiplying it by the number of ships.
The Greeks assumed that the size of ship crews would be fairly evenly spread out between the smallest and largest. Furthermore, it did not matter that the average was not a whole number. In this case, we can see an implicit use of the arithmetic mean. Rather than any observable value to represent the distribution, the Greeks used a purely derived number as the average.
Formulae For Calculating Median
In case of Ungrouped data
Number of data is odd
If we are given n numbers, where n is odd, then the number at the middle will be the median.
That is, Median will be the $\frac^$ observation
Q. Find the median of .
Explanation:
Arranging the elements of the given set in ascending order, we get
Median will be the $\frac^$ observation, i.e. $\frac^$ = $3^$ observation
So, 2 is the median of the given set.
Number of data is even
If we are given n numbers, where n is even, then there will be two numbers at the middle.
Then, Median will be the mean of $\frac^$ and $^$ observations
Q. Find the median of .
Explanation:
Arranging the elements of the given set in ascending order, we get
Median will be the mean of $\frac^$ and $^$ observations, i.e. $\frac^$ and $^$ observations, i.e $3^$ and $4^$ observations
So, the median of the given set = $\frac$ = 4.
In case of Grouped data
If the data is given in form of classes, then:
Median = L + $$ × h
L – lower limit of the median classh – Size of the median class f – frequency of the median classC.F. – Cumulative Frequency of class preceding the median classn – total frequency
Read Also: What Is Selective Pressure In Biology
Solutions To Variational Problems
Several measures of central tendency can be characterized as solving a variational problem, in the sense of the calculus of variations, namely minimizing variation from the center. That is, given a measure of statistical dispersion, one asks for a measure of central tendency that minimizes variation: such that variation from the center is minimal among all choices of center. In a quip, “dispersion precedes location”. These measures are initially defined in one dimension, but can be generalized to multiple dimensions. This center may or may not be unique. In the sense of Lp spaces, the correspondence is:
| Lp |
|---|
- / p =\left\|\mathbf -\mathbf \right\|_:=}\sum _^\left|x_-c\right|^^}
For p = 0 and p = â these functions are defined by taking limits, respectively as p â 0 and p â â. For p = 0 the limiting values are 00 = 0 and a0 = 0 or a â 0, so the difference becomes simply equality, so the 0-norm counts the number of unequal points. For p = â the largest number dominates, and thus the â-norm is the maximum difference.
Empirical Relation Between Measures Of Central Tendency
The three measures of central tendency i.e. mean, median, and mode are closely connected by the following relations .
2Mean + Mode = 3Median
For instance, if we are asked to calculate the mean, median, and mode of continuous grouped data, then we can calculate mean and median using the formulae as discussed in the previous sections and then find mode using the empirical relation.
Example: The median and mode for a given data set are 56 and 54 respectively. Find the approximate value of the mean for this data set.
2Mean + Mode = 3Median
| 0 |
We can observe the histogram for the above-given symmetrical distribution as shown below,
The above histogram displays a symmetrical distribution of data. Finding the mean, median, and mode for this data-set, we observe that the three measures of central tendency mean, median, and mode are all located in the center of the distribution graph. Thus, we can infer that in a perfectly symmetrical distribution, the mean and the median are the same. The above-given example had one mode, i.e, it is a unimodal set, and therefore the mode is the same as the mean and median. In a symmetrical distribution that has two modes, i.e. the given set is bimodal, the two modes would be different from the mean and median.
Also Check: How Long Is Ap Physics 1 Exam
Preparing To Facilitate This Number Talk
This number talk can be facilitated using a chalk/whiteboard or using the visual number talk prompts provided below.
If facilitating this number talk with a chalk/whiteboard, encourage students to talk to their neighbours and compare before they describe where you should plot your data point up on the board. This not only helps students solidify their own understanding of magnitude of number and spatial relationships, but also allows them to build their adaptive reasoning skills as they explain their thinking out loud.
The data points to be plotted on the number line are:
59.5
When To Use The Mean Median And Mode
Weve seen that the mean, median, and mode all measure the central location, or the typical value, of a dataset in very different ways:
Mean: Finds the average value in a dataset.
Median: Finds the middle value in a dataset.
Mode: Finds the most frequently occurring value in a dataset.
Here are the scenarios where certain measures of central tendency are better to use than others:
You May Like: What Is The Equation For Acceleration In Physics
When To Use The Mean
It is best to use the mean when the distribution of the data is fairly symmetrical and there are no outliers.
For example, suppose we have the following distribution that shows the salaries of individuals in a certain town:
Since this distribution is fairly symmetrical and there are no outliers , the mean will do a good job of describing this dataset.
The mean turns out to be $63,000, which is roughly located in the center of the distribution:
The Athenians Wall Conquest
In Greek history, records of the Athenians have shown them using a form of estimation to climb over their enemies fortress walls. To get into the forts of their enemies, Athenians would construct ladders with sufficient height to reach the top of their walls. However, to find the right height, they had their men count the number of bricks in a column of a wall.
Naturally, given the conditions, they returned with many different answers. While naturally some was wrong, it was accepted that the majority had to be right. In this case, we can see an implicit use of mode. The Athenians assumed that the most frequent value had to be correct. This was true even if none of the values represented more than half of the men.
Also Check: How To Calculate Frequency Physics
What Is Central Tendency
Central tendency is a descriptive summary of a dataset through a single value that reflects the center of the data distribution. Along with the variability of a dataset, central tendency is a branch of descriptive statistics.
The central tendency is one of the most quintessential concepts in statistics. Although it does not provide information regarding the individual values in the dataset, it delivers a comprehensive summary of the whole dataset.
Definition Of Measures Of Central Tendency
The Measures of Central tendency are numerical descriptive measures that indicate or locate the center of distribution or set of data. For instance, In a class of 50 students, the average height would be the average height of the class as a whole. Thus, It is also defined as a single value used to describe the center of data.
Recommended Reading: What Are Physical Features In Geography
Skewed Distributions And The Mean And Median
We often test whether our data is normally distributed because this is a common assumption underlying many statistical tests. An example of a normally distributed set of data is presented below:
When you have a normally distributed sample you can legitimately use both the mean or the median as your measure of central tendency. In fact, in any symmetrical distribution the mean, median and mode are equal. However, in this situation, the mean is widely preferred as the best measure of central tendency because it is the measure that includes all the values in the data set for its calculation, and any change in any of the scores will affect the value of the mean. This is not the case with the median or mode.
However, when our data is skewed, for example, as with the right-skewed data set below:
We find that the mean is being dragged in the direct of the skew. In these situations, the median is generally considered to be the best representative of the central location of the data. The more skewed the distribution, the greater the difference between the median and mean, and the greater emphasis should be placed on using the median as opposed to the mean. A classic example of the above right-skewed distribution is income , where higher-earners provide a false representation of the typical income if expressed as a mean and not a median.
When Should You Use The Mean Median Or Mode
The 3 main measures of central tendency are best used in combination with each other because they have complementary strengths and limitations. But sometimes only 1 or 2 of them are applicable to your dataset, depending on the level of measurement of the variable.
- The mode can be used for any level of measurement, but its most meaningful for nominal and ordinal levels.
- The median can only be used on data that can be ordered that is, from ordinal, interval and ratio levels of measurement.
- The mean can only be used on interval and ratio levels of measurement because it requires equal spacing between adjacent values or scores in the scale.
| Levels of measurement |
|---|
Read Also: Who Is Ronan Farrows Biological Father
Finding The Mode For Continuous Data
In the continuous data below, no values repeat, which means there is no mode. With continuous data, it is unlikely that two or more values will be exactly equal because there are an infinite number of values between any two values.
When you are working with the raw continuous data, dont be surprised if there is no mode. However, you can find the mode for continuous data by locating the maximum value on a probability distribution plot. If you can identify a probability distribution that fits your data, find the peak value and use it as the mode.
The probability distribution plot displays a lognormal distribution that has a mode of 16700. This distribution corresponds to the U.S. household income example in the median section.
When to use the mode: Categorical data, Ordinal data, Count data, Probability Distributions
Measures Of Central Tendency: Definition & Examples

A measure of central tendency is a single value that represents the center point of a dataset. This value can also be referred to as the central location of a dataset.
In statistics, there are three common measures of central tendency:
Each of these measures finds the central location of a dataset using different methods. Depending on the type of data youre analyzing, one of these three measures may be better to use than the other two.
In this post, well take a look at how to calculate each of the three measures of central tendency along with how to determine which measure is best to use based on your data.
Recommended Reading: What Is The Geography Of La Paz Mexico
Relation Between Arithmetic Mean And Median
When data in a set is evenly distributed, i.e. the difference between any two consecutive elements of the set is equal , then Median = Arithmetic Mean
For example, consider the numbers 3, 5, 7, 9, 11Difference between any two elements in the above set is 2. So, their median and mean must be equal. Lets check.Mean = /5 = 35/7 = 7Median = the middle value, which is 7.