Distributive Property Definition & Examples
Among all properties in mathematics, the distributive property is used quite often. This is because any method of multiplying numbers by another number uses distributive property. This property was introduced in the early 18th century when mathematicians started analyzing numbers abstracts and properties.
The word distributive is taken from the word distribute, which means you are dividing something into parts. This property distributes or breaks down expressions into the addition or subtraction of two numbers.
What Is A Frequency Distribution In Math
In statistics, the frequency distribution is a graph or data set organized to represent the frequency of occurrence of each possible outcome of an event that is observed a specific number of times. Frequency distribution is a tabular or graphical representation of the data that shows the frequency of all the observations.
A Variety Of Properties
Apart from distributive property, there are other commonly used properties such as the associative property and Commutative property.
Let’s look at the associative property:
The associative property refers to grouping elements together. This rule states that how numbers are grouped within a math problem will not change the product.
Example in addition:
a + = + c or 2 + = + 4
Example in multiplication:
5×4×2 = x 2 = 20 x 2 = 40
This property works with multiplication, addition, subtraction, and division.
You May Like: How Did The Geography Affect The Development Of Greece
Preliminaries: Transpose Of A Linear Operator
Operations on distributions and spaces of distributions are often defined by means of the transpose of a linear operator. This is because the transpose allows for a unified presentation of the many definitions in the theory of distributions and also because its properties are well known in functional analysis. For instance, the well-known Hermitian adjoint of a linear operator between Hilbert spaces is just the operator’s transpose . In general the transpose of a continuous linear map A
In the context of distributions, the characterization of the transpose can be refined slightly. Let A ) }\to }} be a continuous linear map. Then by definition, the transpose of A is the unique linear operator A :}’\to }’} that satisfies:
However, since the image of D it is sufficient that the above equality hold for all distributions of the form T . }.} Explicitly, this means that the above condition holds if and only if the condition below holds:
}\to }} be the partial derivative operator }}.} In order to extend
Therefore Therefore, the partial derivative of T with respect to the coordinate x is defined by the formula
With this definition, every distribution is infinitely differentiable, and the derivative in the direction x is a linear operator on D
is an arbitrary multi-index, then the partial derivative }’} is defined by
If T is a distribution in R
Differential operators acting on smooth functions
Problem of multiplying distributions
Distributive Property With Fractions
Solving algebraic expressions with fractions looks more complicated than it is. Follow the steps outlined below to see how its done.
Hopefully, this step-by-step process helps your students understand how and why the distributive property can come in handy when simplifying fractions and complex numbers.
Note: In steps two and three, we find the LCM and use it to multiply the fractions in order to simplify and get rid of them. Need a quick refresher? See our blog post on how to multiply fractions.
Read Also: Mode In Math Terms
Extensions And Restrictions To An Open Subset
Let ) }} can be extended by zero from its domain V to a function on U by setting it equal to 0 This extension is a smooth compactly supported function called the trivial extension of f and it will be denoted by E } defines the trivial extensionoperator E :}\to },} which is a continuous injective linear map, which is used to canonically identify D as a vector subspace of D . Its transpose #Transpose_of_a_linear_operator” rel=”nofollow”> explained here)
notnotnotextendible to Uextendible
, the restriction to V is neither injective nor surjective. Lack of surjectivity follows since distributions can blow up towards the boundary of V. For instance, if U
)_} be a collection of open subsets of R \in }’} and suppose that for all i \cap U_} is equal to the restriction of T \cap U_} } ). Then there exists a unique T }’} such that for all the restriction of T to U
Let V be an open subset of U. T }’} is said to vanish in V if for all f }} such that \subseteq V} we have 0. T vanishes in V if and only if the restriction of T to V is equal to 0, or equivalently, if and only if T lies in the kernel of the restriction map
)_} be a collection of open subsets of R }’.} T if and only if for each i the restriction of T to U } is equal to 0.
Corollary The union of all open subsets of U in which a distribution T vanishes is an open subset of U in which T vanishes.
Types Of Frequency Distribution
There are four types of frequency distribution under statistics which are explained below:
- Ungrouped frequency distribution: It shows the frequency of an item in each separate data value rather than groups of data values.
- Grouped frequency distribution: In this type, the data is arranged and separated into groups called class intervals. The frequency of data belonging to each class interval is noted in a frequency distribution table. The grouped frequency table shows the distribution of frequencies in class intervals.
- Relative frequencydistribution: It tells the proportion of the total number of observations associated with each category.
- Cumulative frequencydistribution: It is the sum of the first frequency and all frequencies below it in a frequency distribution. You have to add a value with the next value then add the sum with the next value again and so on till the last. The last cumulative frequency will be the total sum of all frequencies.
Recommended Reading: What Happened To Beth Child Of Rage
Types Of Distributive Property
There are three properties of numbers most widely used. They are commutative, associative and distributive property. The distributive property is also known as the distributive law of multiplication. The distributive property is the most frequently used property in mathematics. Distribute means the name itself implies that to divide something.
Distributive property means dividing the given operations on the numbers so that the equation becomes easier to solve. So let us study distributive property definition, distributive property formula, distributive property example and distributive property with variables
Combining Like Terms Using The Distributive Property
Example 1: Distribute then simplify the expression below.
Is it possible to combine the x-terms right away? Not so fast! The term 2x is inside the parenthesis, while 3x is outside. There is no way we can combine them because they are found in different locations.
What we need to do is to first eliminate the parenthesis symbol before we can combine the like terms that would arise either by adding or subtracting. This is where the usefulness of this property comes into play.
At this point, the parenthesis is gone and all x-terms are free to be combined. I would rearrange them by placing similar terms side by side before performing the required operation.
Example 2: Distribute then simplify the expression below.
Since we have two parentheses here, we must apply the property twice. Doing that should get rid of the grouping symbols and allow us to combine like terms.
After eliminating the two parentheses, it is now possible to combine like terms. Make sure to rearrange the terms such that like terms are placed side by side before doing the required operation of addition or subtraction.
Example 3: Distribute then simplify the expression below.
I hope that you can see the pattern now. By having three parentheses, we are required to apply it three times as well.
Since all the terms are outside the parenthesis now, go ahead combining the like terms.
Example 4: Distribute then simplify the expression below.
Solution:
Don’t Miss: Evaluate Homework And Practice Workbook Answers Geometry
Types Of Frequency Distribution Table
There are two types of frequency distribution tables: Grouped and ungrouped frequency distribution tables.
Grouped Frequency Distribution Table: To arrange a large number of observations or data, we use grouped frequency distribution table. In this, we form class intervals to tally the frequency for the data that belongs to that particular class interval.
For example, Marks obtained by 20 students in the test are as follows. 5, 10, 20, 15, 5, 20, 20, 15, 15, 15, 10, 10, 10, 20, 15, 5, 18, 18, 18, 18. To arrange the data in grouped table we have to make class intervals. Thus, we will make class intervals of marks like 0 â 5, 6 â 10, and so on. Given below table shows two columns one is of class intervals and the second is of frequency . In this, we have not used tally marks as we counted the marks directly.
| No. of Students |
|---|
What Is Frequency Distribution
Frequency distribution is used to organize the collected data in table form. The data could be marks scored by students, temperatures of different towns, points scored in a volleyball match, etc. After data collection, we have to show data in a meaningful manner for better understanding. Organize the data in such a way that all its features are summarized in a table. This is known as frequency distribution.
Let’s consider an example to understand this better. The following are the scores of 10 students in the G.K. quiz released by Mr. Chris 15, 17, 20, 15, 20, 17, 17, 14, 14, 20. Let’s represent this data in frequency distribution and find out the number of students who got the same marks.
| Quiz Marks | |
|---|---|
| 14 | 2 |
We can see that all the collected data is organized under the column quiz marks and the number of students. This makes it easier to understand the given information and we can see that the number of students who obtained the same marks. Thus, frequency distribution in statistics helps us to organize the data in an easy way to understand its features at a glance.
Recommended Reading: What Influence Did Geography Play In The Development Of Greek Society
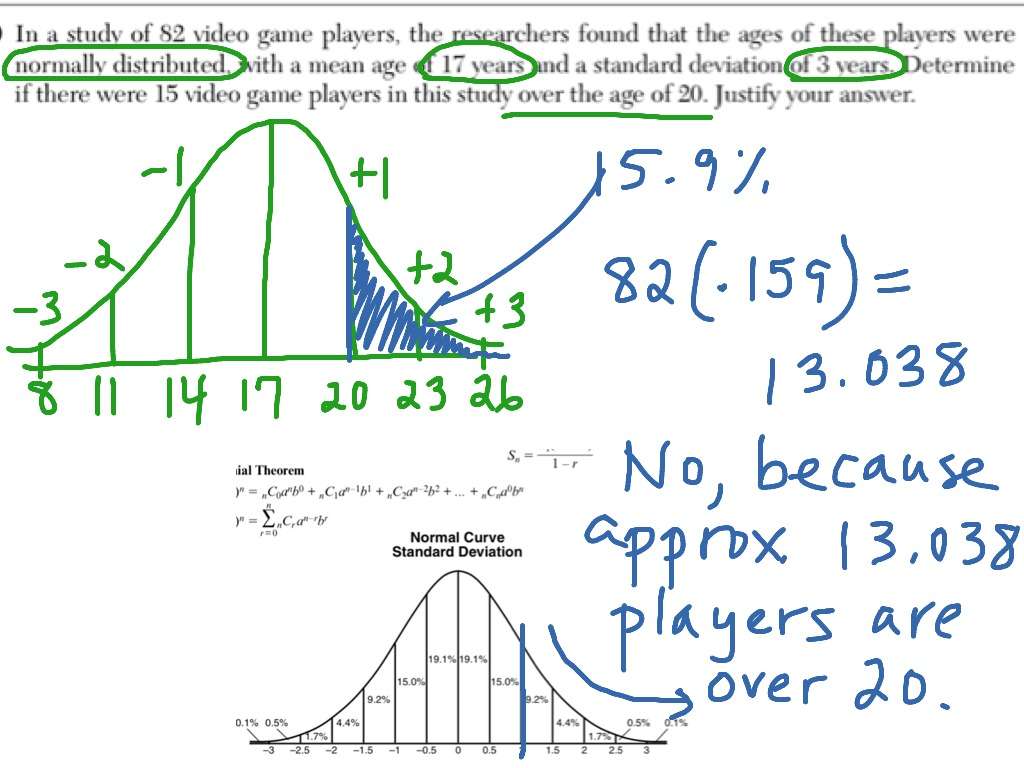
Example: 95% Of Students At School Are Between 11m And 17m Tall
Assuming this data is normally distributed can you calculate the mean and standard deviation?
The mean is halfway between 1.1m and 1.7m:
Mean = / 2 = 1.4m
95% is 2 standard deviations either side of the mean so:
| 1 standard deviation |
| = 0.15m |
And this is the result:
It is good to know the standard deviation, because we can say that any value is:
- likely to be within 1 standard deviation
- very likely to be within 2 standard deviations
- almost certainly within 3 standard deviations
Introduction To Normal Distributions
After completing the readings and exercises assigned for this topic, you should be able to:
Important Note: For help accessing the eText resources referred to below, see Navigating Your eText on the course home page.
Required Reading
Elementary Statistics, Chapter 5, Section 5.1 Introduction to Normal Distributions and the Standard Normal Distribution
Try It Yourself Examples
Work through each Try It Yourself example in this section of the eText. Check your work against the solutions provided.
Exercises in Your eText
Do the following exercises in your eText:
Chapter 5, Section 5.1 Exercises 17, 19, 21, 23, 27, 31. Write out the step-by-step solutions or explanations. Check your work against the solutions provided.
Optional Multimedia Resources
Additional optional multimedia resources related to Chapter 5 Section 5.1 are available on the textbook publishers MyLab website.
Recommended Reading: My.hrw Answers
Normaldist Examples And Recipes
NormalDist readily solves classic probability problems.
For example, given historical data for SAT exams showingthat scores are normally distributed with a mean of 1060 and a standarddeviation of 195, determine the percentage of students with test scoresbetween 1100 and 1200, after rounding to the nearest whole number:
> > > sat=NormalDist> > > fraction=sat.cdf-sat.cdf> > > round18.4
Find the quartiles and for the SAT scores:
> > > list))> > > list))
To estimate the distribution for a model than isnât easy to solveanalytically, NormalDist can generate input samples for a MonteCarlo simulation:
> > > defmodel:... return/...> > > n=100_000> > > X=NormalDist.samples> > > Y=NormalDist.samples> > > Z=NormalDist.samples> > > quantiles)
Normal distributions can be used to approximate Binomialdistributionswhen the sample size is large and when the probability of a successfultrial is near 50%.
For example, an open source conference has 750 attendees and two rooms with a500 person capacity. There is a talk about Python and another about Ruby.In previous conferences, 65% of the attendees preferred to listen to Pythontalks. Assuming the population preferences havenât changed, what is theprobability that the Python room will stay within its capacity limits?
Normal distributions commonly arise in machine learning problems.
Weâre given a training dataset with measurements for eight people. Themeasurements are assumed to be normally distributed, so we summarize the datawith NormalDist:
Probabilities With A Uniform Density Curve
It is important to remember that the height of a curve does not directly indicate the probability of an outcome. Rather, as with any density curve, probabilities are determined by the areas under the curve.
Since a uniform distribution is shaped like a rectangle, the probabilities are very easy to determine. Rather than using calculus to find the area under a curve, simply use some basic geometry. Remember that the area of a rectangle is its base multiplied by its height.
Return to the same example from earlier. In this example, X is a random number generated between the values 1 and 4. The probability that X is between 1 and 3 is 2/3 because this constitutes the area under the curve between 1 and 3.
Read Also: Beth And John Thomas Child Of Rage Now
Distributive Property Of Multiplication Over Addition
Regardless of whether you use the distributive property or follow the order of operations, youll arrive at the same answer. In the first example below, we simply evaluate the expression according to the order of operations, simplifying what was in parentheses first.
Using the distributive law, we:
Lets use a real-life scenario as an example of the distributive property.
Imagine one student and her two friends each have seven strawberries and four clementines. How many pieces of fruit do all three students have in total?
In their lunch bags or, the parentheses they each have 7 strawberries and 4 clementines. To know the total number of pieces of fruit, they need to multiply the whole thing by 3.
When you break it down, youre multiplying 7 strawberries and 4 clementines by 3 students. So, you end up with 21 strawberries and 12 clementines, for a total of 33 pieces of fruit.
How The Order Of Operations Relates
Our understanding of the distributive property comes from the order of operations, commonly known as PEMDAS. When we rewrite expressions to spread out the multiplier, we are actually doing the first step of PEMDAS, which is handling parenthesis.
Let’s take 3 as an example. We could either compute the value first, giving us:
3=3=21.
Or, we could use the distributive property to simplify the expression into 3 + 3:
3+3=6+15=21.
Both methods give us the same answer.
Note: While the commutative property tells us that a is equivalent to a, we usually have the multiplier in front.
You May Like: Get The Message Algebra With Pizzazz
How To Use Distributive Property
In basic operations, the Distributive Property applies to multiplication of the multiplicand to all terms inside parentheses. This is true whether you add or subtract terms:
The Distributive Property allows you to distribute the multiplicands or factors outside the parentheses , to each term inside the parentheses:
– 66
You can use the characteristics of the Distributive Property to break apart something that is too hard to do as mental math, too:
Expand the multiplier and distribute the multiplicand to each place value:
Associate addends for easier mental addition:
16,623
Verification Of Distributive Property
Let us try to justify how distributive property works for different operations. We will apply the distributive law individually on the two basic operations, i.e., addition and subtraction.
Distributive Property of Addition: The distributive property of multiplication over addition is expressed as A × = AB + AC. Let us verify this property with the help of an example.
Example: Solve the expression 2 using the distributive law of multiplication over addition.
Solution: 2 = + 2 + 8 = 10Now, if we try to solve the expression using the law of BODMAS, we will solve it as follows. First, we will add the numbers given in brackets, and then we will multiply this sum with the number given outside the brackets. This means, 2 2 × 5 = 10. Therefore, both the methods result in the same answer.
Distributive Property of Subtraction: The distributive law of multiplication over subtraction is expressed as A × = AB – AC. Let us verify this with the help of an example.
Example: Solve the expression 2 using the distributive law of multiplication over subtraction.Solution: 2 = – 8 – 2 = 6
Now, if we try to solve the expression using the order of operations, we will solve it as follows. First, we will subtract the numbers given in brackets, and then we will multiply this difference with the number given outside the brackets. This means 2 2 × 3 = 6. Since both the methods result in the same answer, this distributive law of subtraction is verified.
Read Also: Span Linear Algebra Example