What Is Slope In Math

How To Find The Slope Of A Line: 3 Easy Steps

You can find the slope of any line by following these three easy steps:

Step One: Determine if the slope if positive or negative

Step Two:Using two points on the line, calculate the rise and the run and express it as a fraction .

Step Three: Simplify the fraction if possible.

Lets take a look at a few examples!

EXAMPLE: Find the slope of the line below.

Step One: Determine if the slope if positive or negative

Notice that the line is increasing from left to right, so we know that this line has a positive slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction .

For this example, lets start by choosing the left farthest point and the right farthest point .

To find rise over run, draw a vertical line that rises from and a horizontal line that runs to , then count how many units you had to travel upward and how many to the right and express it as a fraction as follows:

Rise over run is like building a staircase!

Step Three: Simplify the fraction if possible.

Right now, you can say that the slope of the line is 12/18. But 6/9 is also equivalent to 12/18, so lets see what that would look like on the graph by starting from the first point and this time rising up 6 and running to the right 9 units repeatedly as follows:

Notice how you end up in the same spot!

At this point, it is clear that the line has a slope of 12/18 and a slope of 6/9.

In this example, the slopes of 12/18 and 6/9 can be simplified to 2/3 as follows:

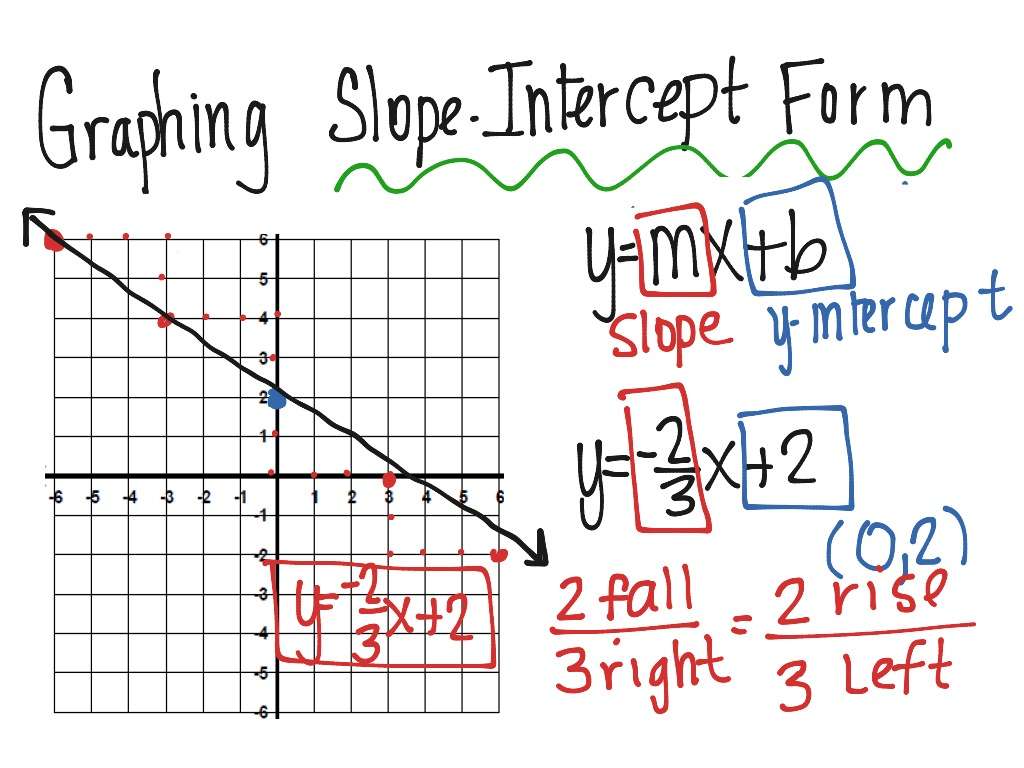
Identify Slope From A Graph

The mathematical definition of slope is very similar to our everyday one. In math, slope is used to describe the steepness and direction of lines. By just looking at the graph of a line, you can learn some things about its slope, especially relative to other lines graphed on the same coordinate plane. Consider the graphs of the three lines shown below:

First, lets look at lines A and B. If you imagined these lines to be hills, you would say that line B is steeper than line A. Line B has a greater slope than line A.

Next, notice that lines A and B slant up as you move from left to right. We say these two lines have a positive slope. Line C slants down from left to right. Line C has a negative slope. Using two of the points on the line, you can find the slope of the line by finding the rise and the run. The vertical change between two points is called the rise, and the horizontal change is called the run. The slope equals the rise divided by the run: \displaystyle \text=\frac}}.

You can determine the slope of a line from its graph by looking at the rise and run. One characteristic of a line is that its slope is constant all the way along it. So, you can choose any 2 points along the graph of the line to figure out the slope. Lets look at an example.

How To Find Slope With Two Points

The easiest way to find slope is to find two coordinate pairs for points on the line. Call these two points and . Note that it does not matter which point is labelled as which.

The formula for slope is: m=.

Remember that slope is rise over run, so you do not accidentally swap the x and y values in the formula.

If a line runs through the points and , label the first point and the second . Then, its slope is:

m==32.

This means that for every two units the line moves to the right, it will move upwards three units.

We can also look at a coordinate plane with two points and find the slope graphically using two points. Consider, for example, the coordinate plane below.

We should first find two points that lie on the line. It makes sense to use the simplest points possible, so the origin and the point make the most sense.

To get from the first point to the second requires us to move up two , over one . Saying this out loud while counting the units gives away the slope. In this case, it is indeed 21, or two over one.

We can double check this by putting the values into the formula above. If is , and is , we have:

m==-2-1=2.

Note that counting graphically to determine slope only works when the data set includes rational numbers that are easy to identify with the graphs scale.

Negative Slope

The two examples above both feature positive slopes. Finding a negative slope, however, is very similar.

m==-5010=-5.

m==50-10=-5.

Zero Slope and Undefined Slope

m==0-1=0.

Recommended Reading: Holt Geometry Workbook Answer Key

What Is A Slope Field

A slope field represents the solutions to a first order differential equation of a scalar function. A series of tic marks indicate slope. The terms slope field and vector field are sometimes used to mean the same thing, but there is an important difference: All the tic marks in a slope field have the same length The marks in vector fields vary in length according to the magnitude of the vector.

Essentially, the slope field contains a series of short, bidirectional lines, each one unit long, and each showing the tangent line of the functions curve at their center points.

Slope fields are also sometimes called direction fields, especially if the vectors retain directional arrows.

The image below shows the slope field of dy/dx = x2 x 2. Three functions are represented by different colors:

• Blue: y = – 2x + 4,
• Red: y = – 2x,
• Turquoise: y = – -2x 4.

Finding The Slope From Two Points On The Line

Youve seen that you can find the slope of a line on a graph by measuring the rise and the run. You can also find the slope of a straight line without its graph if you know the coordinates of any two points on that line. Every point has a set of coordinates: an x-value and a y-value, written as an ordered pair . The x value tells you where a point is horizontally. The y value tells you where the point is vertically.

Consider two points on a linePoint 1 and Point 2. Point 1 has coordinates \left and Point 2 has coordinates \left.

The rise is the vertical distance between the two points, which is the difference between their y-coordinates. That makes the rise \left. The run between these two points is the difference in the x-coordinates, or \left.

So, \displaystyle \text=\frac}} or \displaystyle m=\frac_}-_}}_}-_}}

In the example below, youll see that the line has two points each indicated as an ordered pair. The point is indicated as Point 1, and as Point 2. So you are going to move from Point 1 to Point 2. A triangle is drawn in above the line to help illustrate the rise and run.

You can see from the graph that the rise going from Point 1 to Point 2 is 4, because you are moving 4 units in a positive direction . The run is 2, because you are then moving in a negative direction 2 units. Using the slope formula,

\displaystyle \text=\frac}}=\frac=-2.

The slope, m=\frac-y_}-x_}=\frac=\frac=-2. The slope of the line, m, is 2.

Recommended Reading: Simplifying Radicals Imaginary Numbers Worksheet Kuta Software

Slope Of Horizontal Line

We know that, a horizontal line is a straight line that is parallel to the x-axis or is drawn from left to right or right to left in a coordinate plane. Therefore, the net change in the y-coordinates of the horizontal line is zero. The slope of a horizontal line can be given as,

Slope of a horizontal line, m = y/x = zero

Other Ways To Find Slope

Using given coordinates and then plugging them into the slope equation is the most direct way of finding slope. It is not, however, the only way to do it. Sometimes information given about other lines is a better method.

Parallel Lines

Parallel lines have the same slope, and there are infinitely many lines parallel to a given line. Each line will just cross the x- and y-axes at different points.

For example, the two lines shown below are parallel.

The red line crosses both axes at the origin. The blue line, however, crosses the y-axis at the point . It then crosses the x-axis at the point . Since their slopes are the same, though, they are parallel.

If we know the slope of one line and know that another line is parallel, we can determine the slope of the second line easily.

In the image above, for example, the slope of the red line is easier to find since it passes through the origin. If is , and is , the slope is:

m==-1-4=14.

Since the blue line is parallel, we can bypass the formula. Its slope is also 14.

Perpendicular Lines

Perpendicular lines meet at a 90 degree angle. Like parallel lines, there are infinitely many lines perpendicular to a given line. They will just meet the given line at different points.

The slopes of two perpendicular lines are related. Each is the opposite sign reciprocal of the other.

Recall that the reciprocal is the inverse of a fraction. To find it, simply flip the fraction upside down.

m==-2-3=23.

You May Like: What Does Nc Stand For In Physics

How To Find The Slope Of A Tangent Line Using The Definition Of A Limit

There are several ways to find the slope of a tangent line. The usual way is to take the derivativeIts equal to the slope of the tangent line at any point. However, if youre asked to use the definition of a limit, chances are you havent yet covered how to take a derivative yet in your class. The formal definition of the limit can be used to find the slope of the tangent line:If the point P is on the curve f, then the tangent line at the point P has a slope given by the formula:Mtan = lim h0 f f/h.

Example question: Find the slope of the tangent line to the curve f = 2×2 + 3x 4 passing through the point P.

Step 1: Replace the x in your original function by x + h in the first part of the definition of the limit:mtan = lim h0 + 3 + 4]

Step 2: Subtract your original function and divide by h :mtan = lim h0 / h

Step 3: Solve using algebra. The entire purpose of the following steps is to remove the h from the denominator to prevent division by zero:

This gives you the function for the slope of the tangent line.

Thats it!

What Is The Slope Of A Line

The slope of a line is a number used to describe how steep a line is. This number can be positive, negative, or zero. It can also be rational or irrational.

The slope of a line does not uniquely define it. This means that if you know the slope of a line, you cannot precisely say which points the line runs through.

Parallel lines are any lines that have the same slope. Perpendicular lines are lines that become parallel when one is rotated 90 degrees. If two perpendicular lines cross, they will form four 90 degree angles.

A line with a slope of 0 is a horizontal line. Any line that moves upwards as it goes further to the right is positive. Conversely, any line that moves downwards as it goes further to the left is negative.

A vertical line such as the y-axis is said to have a slope that is undefined. This has to do with how slope is determined mathematically, which we will discuss in more detail below.

You May Like: Geometry Dash Toe2

Mathematics For The Liberal Arts Corequisite

• Find the Slope from a Graph
• Identify rise and run from a graph
• Distinguish between graphs of lines with negative and positive slopes

Slope Of Vertical And Horizontal Lines

The slope of a vertical line is undefined

This is because any vertical line has a $$\Delta x$$ or “run” of zero. Whenever zero is the denominator of the fraction in this case of the fraction representing the slope of a line, the fraction is undefined. The picture below shows a vertical line .

The slope of a horizontal line is zero

This is because any horizontal line has a $$\Delta y$$ or “rise” of zero. Therefore, regardless of what the run is , the fraction representing slope has a zero in its numerator. Therefore, the slope must evaluate to zero. Below is a picture of a horizontal line — you can see that it does not have any ‘rise’ to it.

Do any two points on a line have the same slope?

Answer: Yes, and this is a fundamental point to remember about calculating slope.

Every line has a consistent slope. In other words, the slope of a line never changes. This fundamental idea means that you can choose any 2 points on a line.

Think about the idea of a straight line. If the slope of a line changed, then it would be a zigzag line and not a straight line, as you can see in the picture above.

As you can see below, the slope is the same no matter which 2 points you chose.

You May Like: Geography Movement Definition

What Is Slope And Why Is It Important

Slope can be defined as the angle, inclination, steepness, or gradient of a straight line. Slope often is used to describe the steepness of the grounds surface. Slope can be measured as the rise over the run . Many geographic information systems can analyze digital elevation data and derive both slope and aspect data sets. Slope is an important landscape metric. Some examples of its applications include: to help describe landforms,

Distinguish Between Graphs Of Lines With Negative And Positive Slopes

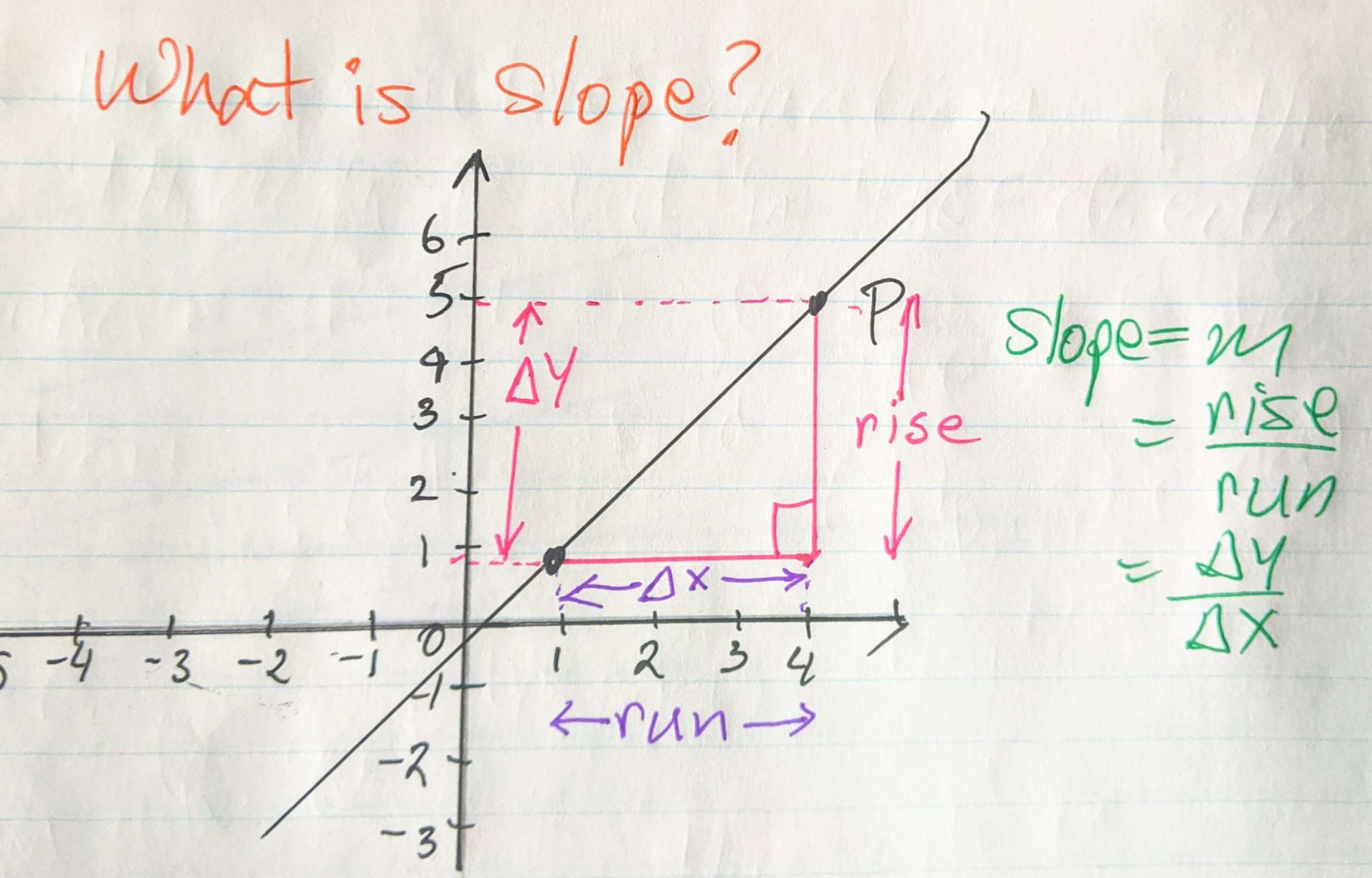
Direction is important when it comes to determining slope. Its important to pay attention to whether you are moving up, down, left, or right that is, if you are moving in a positive or negative direction. If you go up to get to your second point, the rise is positive. If you go down to get to your second point, the rise is negative. If you go right to get to your second point, the run is positive. If you go left to get to your second point, the run is negative.

In the following two examples, you will see a slope that is positive and one that is negative.

Read Also: What Does Ppt Mean In Chemistry

Example #: Find The Slope Of The Line

Step One: Determine if the slope if positive or negative

Notice that the line is increasing from left to right, so we know that this line has a positive slope!

Step Two: Using two points on the line, calculate the rise and the run and express it as a fraction .

In this example, use the two given points as follows:

The rise is 6 and the run is 3.

Step Three: Simplify the fraction if possible.

You should know that 6/3 is equal to 2 . Since we want to think about slope as the fraction rise over run, we can express 2 as 2/1:

Notice that 6/3 reduces to 2/1 or just 2.

You can see that 2/1 is equivalent to 6/3 since the pink staircase on the graph above still gets you to the same point.

So now you can express your answer as follows:

Final Answer: The line has a slope of positive 2.

Why Does The Formula Work

The slope of a straight line is constant. This means that regardless what point we are at on the line, it increases at the same rate for every distance in x along the line, it moves a corresponding, constant, distance in y. We can visualize this using the following image.

The green line segment represents the change in x, and the red line segment represents the change in y. For any horizontal distance, x2 – x1, the line will gain a vertical distance of y2 – y1. This is what “m” in slope intercept form represents.

You May Like: Beth Thomas Rad

Verify Slope From A Dataset

Massive amounts of data is being collected every day by a wide range of institutions and groups. This data is used for many purposes including business decisions about location and marketing, government decisions about allocation of resources and infrastructure, and personal decisions about where to live or where to buy food.

In the following example, you will see how a dataset can be used to define the slope of a linear equation.