Basics Of Geometry Points Line Segment Ray And Line
So lets imagine a blank vacuum of space. Lets make a dot on this blank space, and name the point a. So now we have an object on this blank canvas which we can denote as point a. We can have another point on it called point b Since they are points, they do not connect each other.
Point
Geometrically, we can define a point as a location. It has no size i.e. no width, no length, and no depth. A point is shown by a dot. It has zero dimensions.
Line Segment
Now lets take two other points and call them p and q, so if we connect p and q by starting from p and touch the point q, it is called a line segment. In this line segment, point p and q are called endpoints. Also, we can label or denote this line segment as PQ.
Rays
In the same space where we have the points a and b, as well as the line segment PQ, lets make two points x and y, and connect them. But this time, it originates from x, touches y, and then keeps on going endlessly. Such a structure is called a ray. Since the origin of the ray is x, it will be called a vertex. A ray can be defined as a part of a line that has one endpoint and it extends in one direction endlessly.
Practice 11th CBSE Exam Questions
Lines
Finally, in this space, we have points e and f and we have an object that connected both the points e and f but keeps on going in both directions endlessly, this is known as a line. This line can be denoted as line EF.
What Are Lines And Angles In Geometry
A line is defined as a row of closely spaced dots that extends infinitely in two directions. It has only one dimension, that is its length. An angle is a shape that is formed by the intersection of two line segments, lines, or rays. In other words, when two rays, lines, or line segments intersect each other in the same plane, they form an angle.
What Is A Line
A line has length but no width. A line is a type of geometric figure that can move in both directions. A line is made up of an endless number of points. It is infinite and has no ends on both sides. A line is one dimentional.
In geometry, the notion of line or straight line was introduced by ancient mathematicians to represent straight objects having negligible width and depth. It is often described in terms of two points.
A line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation in the concept of analytic geometry whereas, a line may be an independent object, distinct from the set of points which lie on it in the concept of incidence geometry.
Also read:
Also Check: What Is Hydrostatic Pressure Biology
Frequently Asked Questions About Lines
Lets look at some of the commonly asked questions about lines:
| Question: What is a Line?Answer: In Geometry, a Line is a straight one-dimensional figure having no thickness and extending infinitely in both directions. |
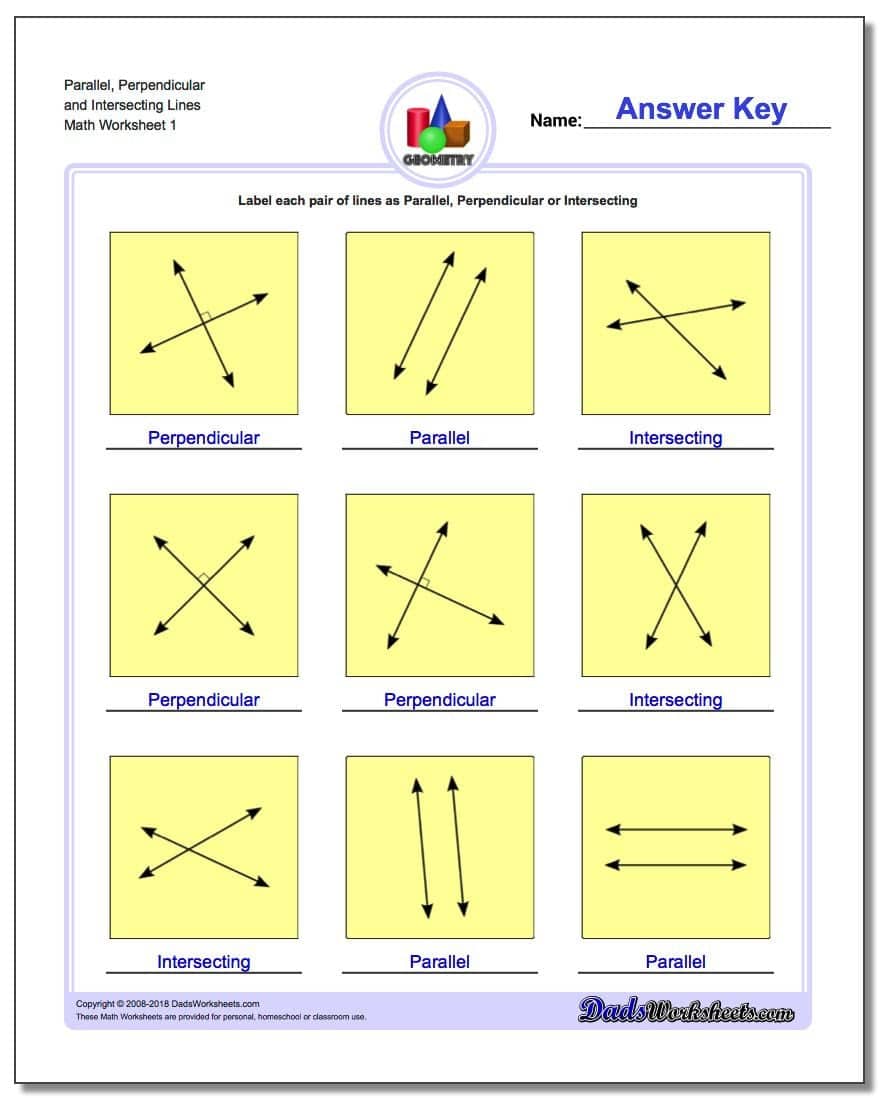
| Question: What are Parallel Lines?Answer: When two distinct lines do not intersect at any point in infinity, they are called parallel lines. |
| Question: What is a line segment? Answer: An object connecting two dots on a plane is called a line segment. |
| Question: What are Perpendicular Lines?Answer: When two lines intersect each other at 90 degrees on the axis, they are called perpendicular lines. |
| Question: Who is the father of Geometry?Answer: Euclid is considered the Father of Geometry. |
Line: Definition Diagrams Types And Examples
In geometry, it is common to say a line segment and lines are the same. A Line segment has a definite beginning and a definite end, but a line is extended towards infinity at both ends. Examples of line segments include the length of a table, the distance of a straight road, etc. A segment is part of a line, but a line is not part of a segment. Lets learn about lines, their types and some real-life examples.
Horizontal, vertical lines, parallel and perpendicular lines are examples of different types of lines. A line is a one-dimensional figure, which has length but no width. A line is made up of a series of points that are infinitely stretched in opposite directions. Two points in a two-dimensional plane determine it. Collinear points are two points that are located on the same line. Continue reading this article to know more about Line.
| Latest Update:? The CBSE Term 1 results are expected to be released in January 2022.? The Term 2 examination will commence in March/April. The board will soon release the admit card and exam date sheet in February 2022. |
You May Like: What Are The Themes Of Geography
Different Types Of Lines In Geometry Basic Definition And Examples
A line is a one-dimensional geometric figure having length but no width. It is made up of points that are extended in opposite directions infinitely. The different types of lines are horizontal, vertical, parallel, perpendicular, curved, and slanting lines. The definitions of each type of line with an image are given below. Go through the entire article to learn in detail about the Types of Lines in Geometry and examples for each one of them.
Properties Of Parallel Lines
If two lines are intersected by a transversal,pair of acute anglesare equal in measure, pairs of obtuse angles are also equal inmeasure,and any acute angle is supplementary to any obtuse angle.
If line m is || to line n, then:
Alternate interior angles will be equal in measure.
Corresponding angles will be equal in measure.
The sum of degree measures of two interior angles on the same side of the transversal is 180.
Also, the sum of the degree measures by any acute angle and any obtuse angle will be 180.
Read Also: The Algebra Of Happiness Amazon
The Derivatives Of Straight Line
-
A straight line at right angles to another line is called as the perpendicular.
-
A straight line that is limiting the value of the curve is called as asymptote.
-
A straight line that just touches a curve at a particular point but does not intersect it at that point is called as the tangent.
-
A straight line that intersects the curve at two or the more points is called as the secant.
-
A straight line from the center to the perimeter of the circle is called as the radius.
-
A straight line connecting two points on a curve is a chord.
-
A straight line relating any two vertices of a polygon that are not adjacent is a diagonal.
Axiomatic Basis Of Non
Euclidean geometry can be axiomatically described in several ways. Unfortunately, Euclid’s original system of five postulates is not one of these, as his proofs relied on several unstated assumptions that should also have been taken as axioms. Hilbert’s system consisting of 20 axioms most closely follows the approach of Euclid and provides the justification for all of Euclid’s proofs. Other systems, using different sets of undefined terms obtain the same geometry by different paths. All approaches, however, have an axiom that is logically equivalent to Euclid’s fifth postulate, the parallel postulate. Hilbert uses the Playfair axiom form, while Birkhoff, for instance, uses the axiom that says that, “There exists a pair of similar but not congruent triangles.” In any of these systems, removal of the one axiom equivalent to the parallel postulate, in whatever form it takes, and leaving all the other axioms intact, produces absolute geometry. As the first 28 propositions of Euclid do not require the use of the parallel postulate or anything equivalent to it, they are all true statements in absolute geometry.
To obtain a non-Euclidean geometry, the parallel postulate must be replaced by its negation. Negating the Playfair’s axiom form, since it is a compound statement , can be done in two ways:
You May Like: Is Love An Emotion Psychology
Lines: What Is A Line
Definition of Line: Casey, 1893 defined a line as a straight one-dimensional figure having no thickness and extending infinitely in both directions. A line is sometimes called a straight line or, more archaically, a right line. To understand lines properly, lets look at some of the rules that a line follows:
- It is a straight set of points that extends in opposite directions.
- It has no ends in both directions.
- It has no thickness.
What Are The Properties Of Lines And Angles
Since there are different kinds of lines and angles, each of them has different properties. However, there are some common properties of lines and angles that can be listed.
Properties of Lines
- Lines can be defined as a set of an endless number of points close to each other.
- They extend infinitely in both directions.
- They are one-dimensional and do not have any depth or thickness.
Properties of Angles
- An angle is a geometrical figure that is formed when two lines intersect each other in the same plane.
- The lines that form an angle are termed as its arms and the point at which they form the angle is called its vertex.
Don’t Miss: Geometry Chapter 10 Test Form 2b
Properties Of Lines And Angles
As we have seen that there are different kinds of lines and angles, each of them has different specific properties. However, there are some basic common properties of lines and angles that can be discussed.
Properties of Lines
- Lines can be defined as a set of an infinite number of points close to each other.
- They extend infinitely in both directions.
- They are one-dimensional and do not have any depth or thickness.
Properties of Angles
- An angle is a geometrical figure that is formed when two lines intersect each other in the same plane.
- The lines that form an angle are termed as its arms , and the point at which they form the angle is called its vertex.
Basic Geometry: Types Of Linesposted On : 12

The lines are the geometrical one dimensional object with no curve. One dimensional in the sense they have only one dimension, length and no breadth or depth. They are long and straight geometric figures which extend in both the directions. Greek Mathematician Euclid defined line as “breadthless length”.
You May Like: Simplifying Rational Expressions Practice Algebra 2
Tips On Lines And Angles
Here is a list of a few tips that should be remembered while studying lines and angles:
- All geometry shapes have angles and lines in them.
- A line is a one-dimensional figure, with no breadth, and that extends in both directions infinitely.
- These are the lines with one end as the start point and the other end going to infinity. These are used to form angles.
- Angles are formed when two rays intersect at a point.
Related Topics
Check out these interesting articles to learn more about the properties of lines and angles, and their related topics.
Lines: Types Of Lines
When we study geometry, we will come across different types of lines. Lets look at the 4 basic types of lines:
Horizontal Lines
When a line moves on a horizontal direction from left to right or vice versa it is called a horizontal line. In the below image, line XY is a horizontal line.
Vertical Lines
When a line moves on a vertical direction from top to bottom or bottom towards the top, it is called a vertical line. In the below image, the line PQ is a vertical line.
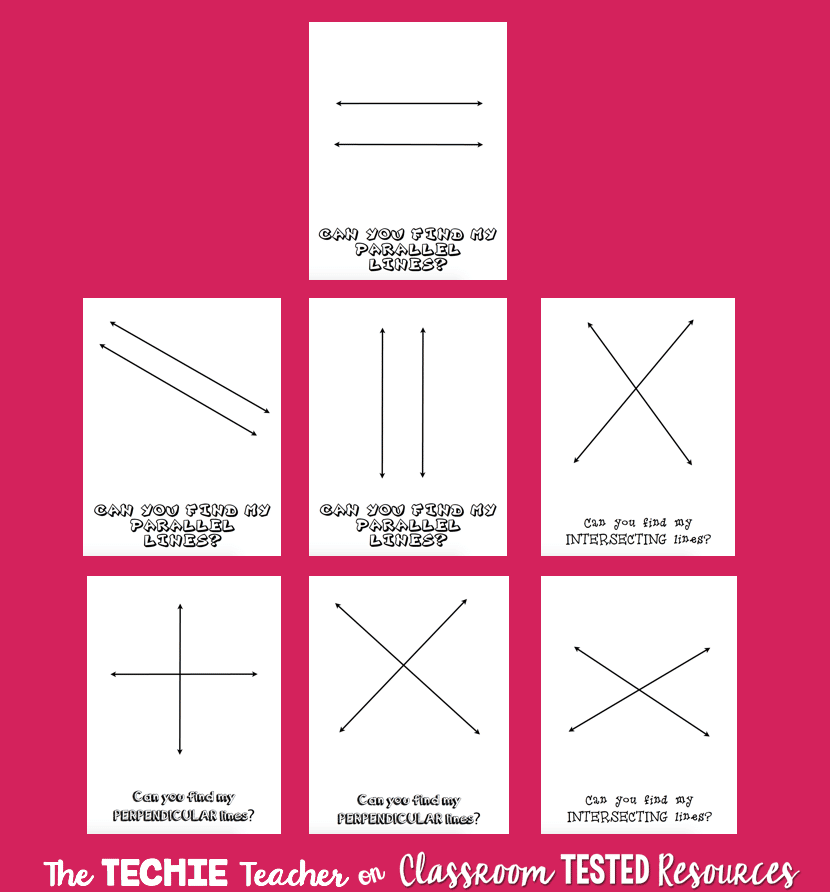
Parallel Lines
When two distinct lines are equidistant to each other and do not intersect at any point till infinity, they are called parallel lines. In the above image, lines EF and GH are parallel lines.
Perpendicular Lines
When two lines meet each other at an angle of 90 degrees, they are called perpendicular lines. In the above image, lines AB and CD are parallel lines.
Read Also: What Math Classes Do You Need For Computer Science
What Are The Different Types Of Lines And Angles
There are different types of lines and angles in geometry. The six types of angles are right angle, acute angle, obtuse angle, straight angle, reflex angle, and complete angle. The different types of lines are horizontal lines, vertical lines, parallel lines, perpendicular lines, and transversal lines.
Lines Segments And Rays
Although we all know intuitively what a line is, it is actually difficult to give a good mathematical definition. Roughly, we can say that a line is an infinitely thin, infinitely long collection of points extending in two opposite directions. When we draw lines in geometry, we use an arrow at each end to show that it extends infinitely.
A line can be named either using two points on the line or simply by a letter, usually lowercase .
A line segment has two endpoints. It contains these endpoints and all the points of the line between them. You can measure the length of a segment, but not of a line.
A segment is named by its two endpoints, for example, A ¯ .
A ray is a part of a line that has one endpoint and goes on infinitely in only one direction. You cannot measure the length of a ray.
A ray is named using its endpoint first, and then any other point on the ray (for example, B
Also Check: What Does Theta Mean In Math
Definition Of Line Segment
In mathematics, line segment and line are essential concepts for constructing geometrical shapes. In geometry, a line segment is the part of the line with a fixed distance. We can say that the line segment has a finite length, whereas the line does not have any fixed size.
As per Euclids concept, a line is a breadthless length. A line is an essential geometric figure, which connects all points on it. A line has no endpoints, and it extends infinitely in both directions. A line segment is a part of the line. A line segment connects any of the two points on the line. The part or portion of the line between points \ and \ is called the line segment in the figure below. Thus, \ is the line segment.
The line segment is connected way of the two points, which you can measure. Line segments are utilised to form the sides of the polygon.
Definition Of Lines And Angles
As we have discussed, both lines and angles form the base for any shape in geometry. We cannot draw a two-dimensional to three-dimensional shape without using lines and angles. Thus, it is very necessary to learn the definitions of both terms.
Here, the basic definitions and properties of lines and also for angles are given. It will give the students a basic knowledge of these geometrical terms.
Recommended Reading: What Does Mole Mean In Chemistry
Standard Form Of Equation Of A Line
The standard form of a line is in the form Ax + By = C, where A, B, and C are integers, it gives all of the same information as the slope-intercept form, y = mx + c.
-
The equation of a straight line parallel to the x-axis
The line y = k is parallel to the x-axis lies above or below the x-axis according to k which is positive or negative.
The equation of the straight line parallel to the x-axis is independent of x.
-
The equation of a straight line parallel to the y-axis
The line x = k is parallel to the y-axis lies right or left of the y-axis according to whether k is positive or negative. The equation of the straight line that is parallel to the y-axis is independent of y.
-
The slope-intercept form
The equation of a straight line is y = mx + c. It has a slope m and makes an intercept c on the y-axis.
-
The Point-Slope Equation of a Line
The equation of a straight line passing through a fixed point and having a given slope m is called a point-slope form.
= m, is the general equation of the straight line passing through the fixed point and having slope m.
-
The equation of Line from Two Points
The equation of a straight line going through two fixed points is also called a two-point form.
= m is the general equation of a straight line passing through the fixed points , and having slope m.
where, \
Solved Examples On Lines
Throughout the article, we learn about various terms like a line segment, ray, point and angle relation, various types of line with images, the general equation, slope followed by the equation of a line in different forms. Let us rehearse some solved examples for more practice of the topic.
Question 1: How to calculate the distance between the lines 3x + 4y = 9 and 6x + 8y = 18.
Solution: The lines are parallel if their slopes are equal, i.e \ or.
The distance between two parallel lines is given by the equation:
Calculation:
Given: 3x + 4y = 9 and 6x + 8y = 18.
These equations can be expressed as :
Here, m = 3 / 4 and \
Hence, d = 0.
Question 2: What is the equation of the straight line passing through and ?
Solution: In two points form:
The equation of a line passing through two points is given by:
\=\frac\left\)
Calculation:
Given: and
Here, \
As we know that, the equation of a line passing through the points \\text\) is given by:
\=\frac\left\)
\=\frac\left=-1\left\Rightarrow x+y=3\)
Question 3: Which of the below statements are true.
Solution:
The first statement is true as per the definition.
The second is false, as any polygon is made of lines and not rays.
The third is false, as per the definition of line.
Don’t Miss: What Is Conscientiousness In Psychology