How To Find Tension
The following are the steps to get the tension of a rope easily.
- Make a note of the given details in the question.
- If the object is hanging to one rope, then multiply the mass of the object with the acceleration due to gravity to get the tension of rope.
- When the object is pulling on a frictionless surface, then multiply the cos of angle and tension force.
- Divide the product by cos of other angle to find the tension.
Cylinder Equations To Solve Pulley Tension Problems
Only one equation and that is along Y-axis.W2 T = maNow combining equation 2 and 3, we getmg Ma = maor, a = / Here in equation 4, we get the expression of the acceleration of the cylinder and the cart.Now again from equation 2 and 4 we get a complete expression of the tension T in the rope. T = Ma = M . /or, T = / .
So the acceleration of the cart is = /And the tension in the rope is /
In What Cases Would The Force Of Tension Between Two Bodies Connected By The Same Rope Differ
The rope acts as a transferring agent of the force, so there should never be a scenario in which two objects connected by one rope experience tension forces of different magnitudes.
Stay tuned to BYJUS and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Read Also: What Does Relativity Mean In Physics
Qhow To Find Tension In A Pulley System
In a pulley system the total force equals the tension in the rope and the gravity force pulling at the load.
A pulley is a rotating wheel having curved rim which is connected to a rope, string or a cable. It simply reduces the energy and the power required to lift heavy objects. The tension force in such case is calculated using the formula T = M x A .
Force Of Tension In Pulley Systems
A common category of physics problem involving tension involves a pulley system. A pulley is a circular device that spins to let out a rope or string.
Usually high school physics problems treat pulleys as massless and frictionless, though in the real world this is never true. The mass of the rope typically gets ignored as well.
Don’t Miss: What Is Ucs In Psychology
How To Find The Force Of Tension
To find the force of tension on an object, draw a free-body diagram to see where this force must apply . Then find the net force to quantify it.
Note that tension is only a pulling force. Pushing on one end of a slack rope doesn’t cause any tension. Therefore, the force of tension in a free-body diagram should always be drawn in the direction that the string is pulling on the object.
In the tire-swing scenario as mentioned previously, if the tire is still that is, not accelerating upwards or downwards there must be a net force of zero. Since the only two forces acting on the tire are gravity and tension acting in opposite directions, those two forces must be equal.
Mathematically: Fg= Ft where Fg is the force of gravity, and Ft is the force of tension, both in newtons.
Recall that the force of gravity, Fg, is equal to an object’s mass times the acceleration due to gravity g. So Fg= mg = Ft.
For a 10-kg tire, the force of tension would thus be Ft = 10 kg × 9.8 m/s2 = 98 N.
In the same scenario, where the rope connects with the tree branch there is also zero net force. At this end of the rope, however, the force of tension in the free-body diagram is directed downwards. However, the magnitude of the force of tension is the same: 98 N.
From this, the upwards contact force that the branch is applying on the rope must be the same as the force of tension downwards, which was the same as the force of gravity acting downwards on the tire: 98 N.
Dimensional Formula Of Tension
Tension is a type of force that acts along the length of the medium such as rope or string. A force is necessary to put these objects under tension. Tension is also named something exciting, i.e. action-reaction pair.
The Tension Dimensional Formula =
Tension is nothing, but its a force that has got another improved name. Tension acts at both the end of the string . The tension force is available on each point of the string.
Read Also: What Does W Stand For In Physics
Write The Equation Of Forces In A Pulley
The forces acting on the pulley due to the object of mass M1 is
F=T-M_1g
-M_1a=T-M_1g
T= M_1g -M_1a –
The force due to gravity is applied in the negative y-direction hence we have taken it as negative and the tension is exerted in the upward direction in the positive y-direction. The acceleration of the mass is also in the downward direction.
The forces acting on the pulley due to the object of mass M2 is
F=T-M_2g
M_2a=T-M_2g
T=M_2g+M_2a –
The acceleration of both the masses on the pulley will be at the same rate but only the direction of motion differs.
Physics Definition Of Tension
Tension is a contact force transmitted through a rope, string, wire or something similar when forces on opposite ends are pulling on it.
For example, a tire swing hanging from a tree causes tension in the rope holding it to the branch. The pull on the bottom of the rope comes from gravity, while the upwards pull is from the branch resisting the rope’s tug.
The force of tension is along the length of the rope, and it acts equally on objects at both ends the tire and the branch. On the tire, the force of tension is directed upwards while on the branch, the force of tension is directed downwards .
Don’t Miss: Algebra Eoc Practice Test 3 Answers
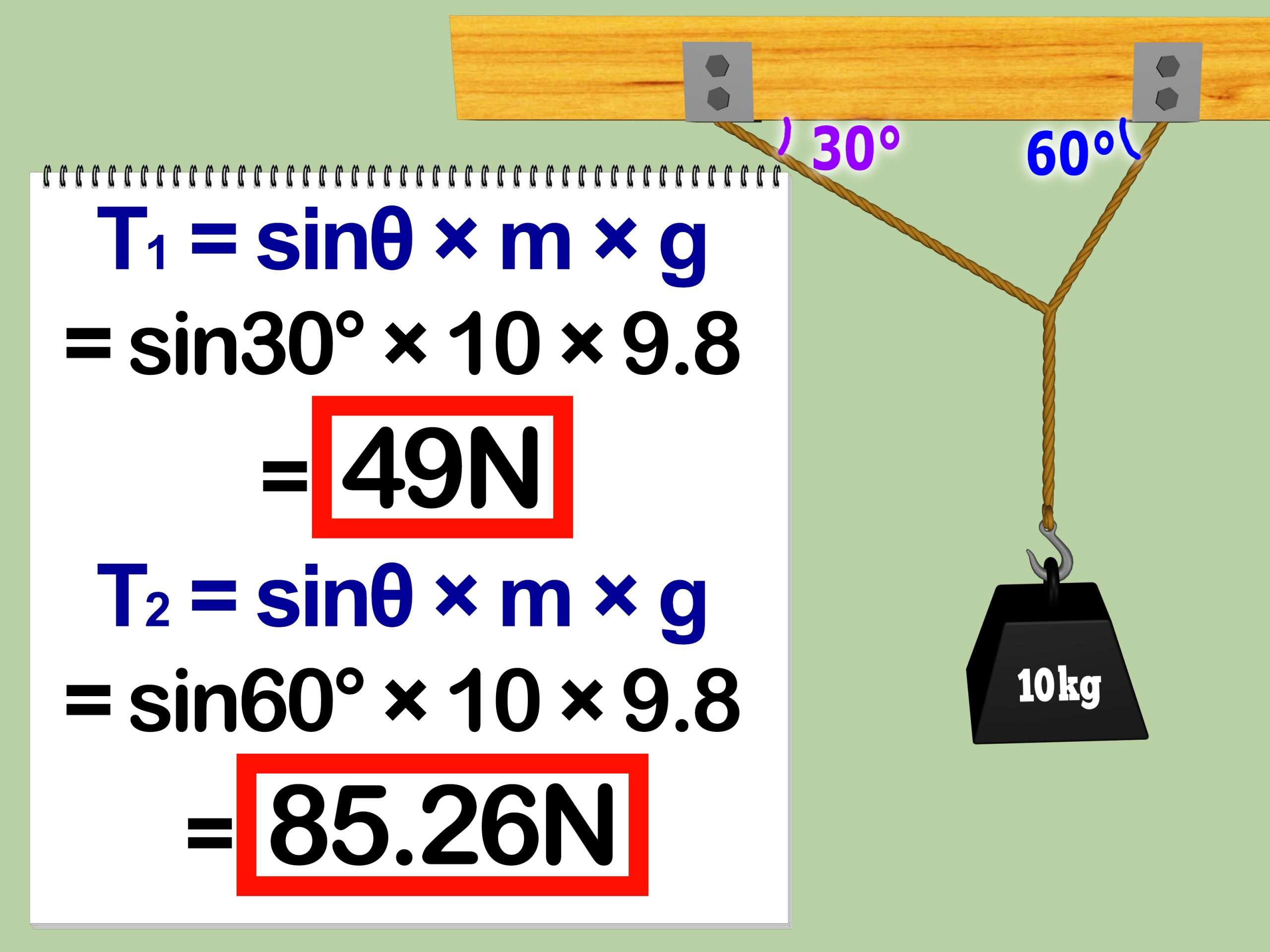
The Formula For Tension In A Rope Attached To A Weight At An Angle
Tensionforce is developed in a rope when a weight is attached to it. The tension developed in the rope should be equal to the gravitational pull on the weight. But this is true only for a case when the rope is vertically suspended. The formula for tension also depends on the angle of suspension. Here in this article, we look at the examples, formulas, and numerical problems for tension when the rope is suspended at an angle to the ceiling.
The weight of mass m is suspended by two ropes with tension T1 and T2. The tension in both the ropes will be different, so we have to derive two separate sets of the formula for tensions in both strings. Since the weight is static, the net forces acting on the weight in the x and y direction should be zero.
We will start by drawing a free-body diagram and resolve the forces in x and y directions.
Resolving the forces in y-direction: The forces acting in the y-direction are a downward gravitational pull and component of tension forces T1 and T2 in an upward direction. Equating the force we get:
T1 sin + T2 sin = m*g –
Resolving the forces in x-direction: The forces acting in the x-direction are the components of tension forces T1 and T2 in opposite directions. Equating the forces we get:
T1cos = T2cos
Solving equations and , we get the formula for tension.
T1 = /cos]
T2 = /cos]
Facts About Tension Force
You May Like: Geometry Area Apothem Worksheet Answers
Optional: Real Forces And Inertial Frames
There is another distinction among forces in addition to the types already mentioned. Some forces are real, whereas others are not. Real forces are those that have some physical origin, such as the gravitational pull. Contrastingly, fictitious forces are those that arise simply because an observer is in an accelerating frame of reference, such as one that rotates or undergoes linear acceleration . For example, if a satellite is heading due north above Earths northern hemisphere, then to an observer on Earth it will appear to experience a force to the west that has no physical origin. Of course, what is happening here is that Earth is rotating toward the east and moves east under the satellite. In Earths frame this looks like a westward force on the satellite, or it can be interpreted as a violation of Newtons first law . An inertial frame of reference is one in which all forces are real and, equivalently, one in which Newtons laws have the simple forms given in this chapter.
Earths rotation is slow enough that Earth is nearly an inertial frame. You ordinarily must perform precise experiments to observe fictitious forces and the slight departures from Newtons laws, such as the effect just described. On the large scale, such as for the rotation of weather systems and ocean currents, the effects can be easily observed.
How Do I Calculate The Tension Of A Rope At An Angle
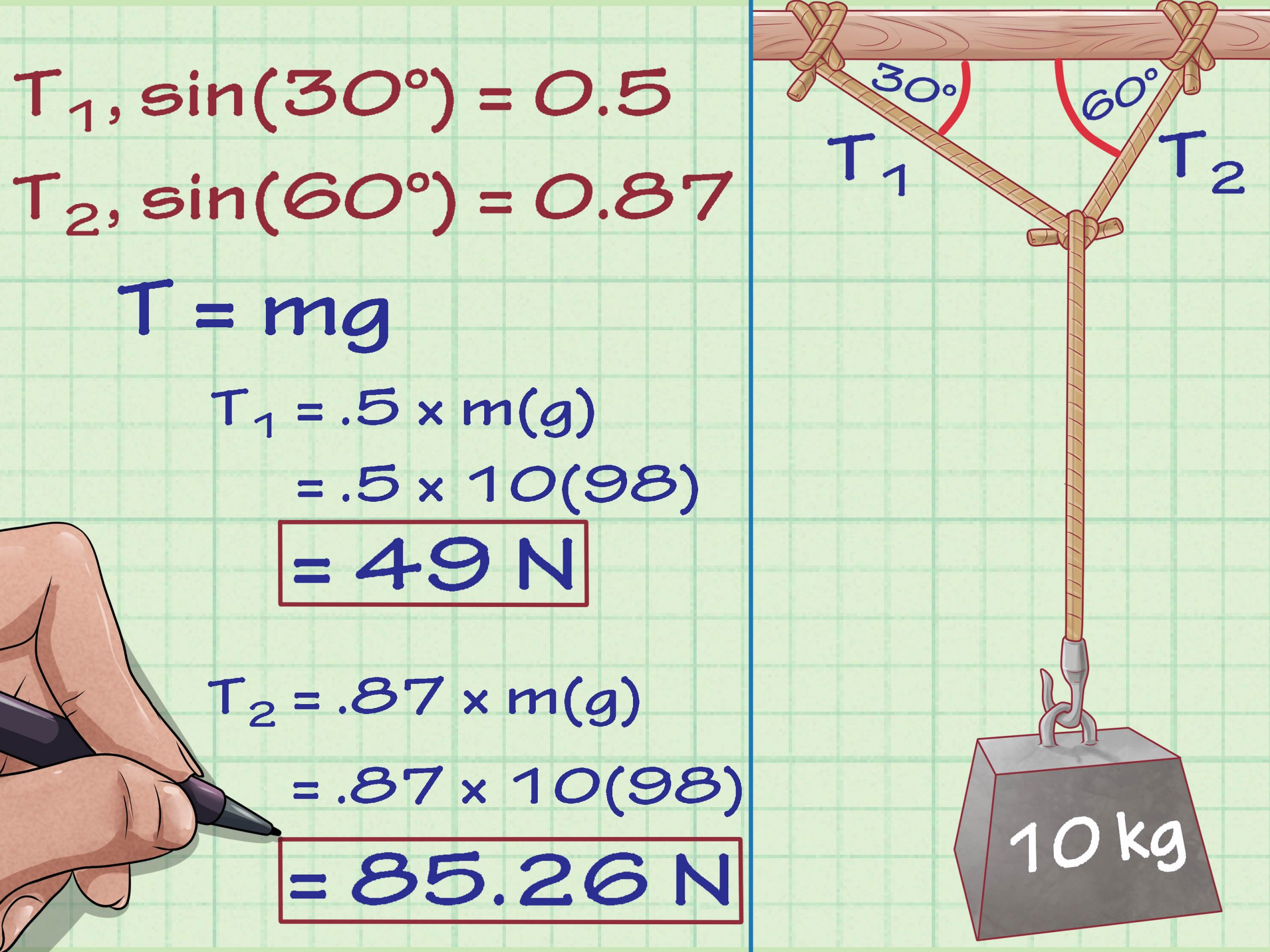
To calculate the tension of a rope at an angle:
You May Like: Algebra 1 Test 3 Answers
Force Of Tension In Two Dimensions
Consider a hanging pot rack. There are two ropes holding up a 30-kg rack, each at an angle of 15 degrees from the corners of the rack.
To find the tension in either rope, the net force in both the x- and y-directions must be balanced.
Start with the free-body diagram for the pot rack.
Of the three forces on the rack, the force of gravity is known, and it must be balanced equally in the vertical direction by both of the vertical components of the forces of tension.
and because FT1,y= FT2,y :
In other words, each rope exerts a force of 147 N upwards on the hanging pot rack.
To get from here to the total force of tension in each rope, use trigonometry.
The trigonometric relationship of sine relates the y-component, the angle and the unknown diagonal force of tension along the rope on either side. Solving for the tension on the left:
This magnitude would be the same on the right hand side as well, though the direction of that force of tension is different.
What about the horizontal forces each rope exerts?
The trigonometric relationship of tangent relates the unknown x-component to the known y-component and the angle. Solving for the x-component:
Because the horizontal forces are also balanced, this must be the same magnitude of force exerted by the rope on the right, in the opposite direction.
Related Articles
S On How To Find Tension Force With Acceleration:
Consider an object O of mass m kg suspended from a point. Assume that the object is accelerating up or down with an acceleration of a \inline m/s^.
Our initial step is to construct a free body diagram. This diagram illustrates the different types of forces along with the direction in which these forces acts.
Since the body is suspended, the force of gravity is the primary force acting on it. The expression for the gravitational force acting on any object of mass M kg is given by
F = Mg
where g is the acceleration due to gravity whose value is 9.8 \inline m/s^. This expression is a result of the Netwons second law of motion which says that net force is given by the product of a bodys mass and its acceleration.
So here, the weight acting on the body W is given by
W = Mg
and is directed downwards.
Let T be the tension force acting along the string. Now we use Newtons third law of motion to find the Tension force in the system. The third law states that
To every action, there is an equal and opposite reaction.
The summation of all upward forces must be equal to the summation of all downward forces if the system was in equilibrium.
Now, Newtons second law of motion is applied since the body is accelerating. Hence, the Tension force T is given by
T = W \pm ma
There are a few cases:
The basic assumptions made here are: the rope or string is massless and the motion is frictionless.
Don’t Miss: What Is The Biological Species Concept
Determining Tension On A Single Strand
Solved Examples On Tension Formula
Q.1. A \ mass is dangling at the end of a thread. If the acceleration of the mass is acting as: \ in the upward direction. \ in the downward direction.Calculate the tension in the thread.Ans: We are given:Mass of the hanging body, \\\ When the body is accelerating upwards, the tension force is\ When the body is travelling downwards, the tension force is:\\\)\
Q.2. A monkey climbs up a cable tied to a tree with an acceleration \. If the mass of the monkey is \. Find the tension in the cable. Take \.Ans: We are given,Mass of monkey: \Acceleration of monkey: \The tension in the cable will be equal to the apparent weight of the monkey, thus:\\
Also Check: What Is Activation Energy Biology
How Do We Calculate The Force Of Tension
The tension on an object is equal to the product of the mass of the object and gravitational force added to the product of the mass and acceleration. Mathematically, it is represented as follows: T = mg + ma Let us look at the solved example to better understand.
1. There is a 10 kg mass hanging from a rope. What is the tension in the rope if the acceleration of the mass is zero?
Solution:We know that the force of tension is calculated using the formula T = mg + ma.Substituting the values in the equation, we get T= + T = 108 NNow, assume that there is an acceleration +5 m/s2 upwards. Substituting, we get T= + T=148 N Assume a downwards acceleration of a = -5m/s2Substituting, we get T= + T= 48 N
Therefore, the work done by tension is zero.