Angle Bisector Theorem Formula
Triangle angle bisector theorem states that “In a triangle, the angle bisector of any angle will divide the opposite side in the ratio of the sides containing the angle”. From this, we can write the triangle angle bisector theorem formula as,
Related Topics
Listed below are a few interesting topics related to the triangle angle bisector theorem, take a look.
Internal Angle Bisector Theorem
An angle bisector of a triangle divides the opposite side into two segments proportional to the other two sides of the triangle. In the triangle \ the angle bisector intersects side \ at point \
As per the angle bisector theorem, the ratio of the line segment \ to \ is equal to the ratio of the length of the side \ to \
Draw a line \ from point \ parallel to \
The line \ intersects the extended line \ of a triangle at \
From the figure,\ and \ is transversal, and we know that alternate interior angles formed by a transversal are equal.
\ \\)
Similarly, \ and \ is transversal. We have\ \\)
Given, \ is the angle bisector of \\\)
From \, \) and \,\) we have \
Hence, \ is an isosceles triangle.
So, in \ we have \ According to the basic proportionality theorem, if a line is drawn parallel to one side of the triangle, then it divides the other two sides in the same ratio.
Now, in BCE we have,\.\
As, \ then the ratio becomes
Any Point On The Bisector Of An Angle Proof
The following is the proof for any point on the bisector of an angle is equidistant from the arms of the angle.
- Let us take a triangle ABC.
- Draw angle bisector BZ that bisects ABC.
- Draw two lines OL AB, OM BC.
So, we have to prove that OM = OL.
Now we can observe two triangles BOL, BOMBZ bisects ABC. So, LBO = OBMIt is given that, BLO = BMO = 90°The common vertex for both triangles is OB. So, OB = OBBOL BOM by the AAS criterionSo, OM = OL
Read Also: Sf5+ Lewis Structure
Definition And Statement Of Angle Bisector Theorem
The Angle Bisector Theorem helps in finding unknown lengths of sides of triangles because an angle bisector divides the side opposite that angle into two segments that are proportional to the triangles other two sides.
In other words, it states that if a point is on the angle bisector of an angle in a triangle, then the point is equidistant from the sides of the angle.
Angle Bisector Of A Triangle

In a triangle, the angle bisector of an angle is a straight line that divides the angle into two equal or congruent angles. There can be three angle bisectors in every triangle, one for each vertex. The point where these three angle bisectors meet in a triangle is known as its incenter. The distance between the incenter to all the vertices of a triangle is the same. Look at the image below showing the angle bisector of a triangle. Here, AG, CE, and BD are the angle bisectors of BAC, ACB, and ABC respectively. F is the point of intersection of all three bisectors which is known as incenter and it is at an equal distance from each of the vertex.
Recommended Reading: Algebra 1 Week 1 Fsa Countdown Answers
Angle Bisector Of Triangle Definition
An angle bisector is a ray that divides a given angle into two angles with equal measures. We usually divide an angle in a triangle by a line or ray, which is considered an angle bisector. Bisecting an angle means drawing a ray in the interior of the angle, with its initial point at the vertex of the angle such that it divides the angle into two equal parts.
Example: Consider an angle \. An angle bisector divides it into two equal angles of \.
Construction Of Angle Bisector
Follow the steps given below for constructing an angle bisector with an example
1. Step \ Draw any angle, say \.
2. Step \ Taking \ as the centre and any appropriate radius, draw an arc to intersect the rays \ and \ at, say, \ and \ respectively.
3. Step \ Now, taking \ and \ as centres and with a radius more than half of \ draw an arc to intersect each other at \
4. Step \ Draw ray \ This ray \ is the required angle bisector of angle \
Recommended Reading: Paris Jackson Biological Parents
Converse Of Angle Bisector Theorem
The converse of angle bisector theorem states that if the sides of a triangle satisfy the following condition “If a line drawn from a vertex of a triangle divides the opposite side into two parts such that they are proportional to the other two sides of the triangle”, it implies that the point on the opposite side of that angle lies on its angle bisector. Here, it is known to us that sides are in proportion, and from this, we came to a conclusion that the line/ray/segment is the angle bisector of the respective angle. This is known as the converse of angle bisector theorem in geometry.
Look at the image below to understand it visually.
Internal And External Bisector Of An Angle Of Triangle
The bisector of a triangle that divides the opposite side internally in the ratio of corresponding sides containing angles is known as the internal bisector of an angle of a triangle.
The bisector of a triangle that divides the opposite side externally in the ratio of corresponding sides containing angles is known as the external bisector of an angle of a triangle.
Don’t Miss: Is Physics Or Chemistry Harder
Solved Examples Angle Bisector Theorem
Q.1. In \ if \ bisects \ Find the value of \?
Ans: Given that, \ is the bisector of \According to the angle bisector theorem: \\\ = \)\\\
Q.2. Mrudula has drawn a right-angled triangle as shown below, and she asks Cherry to determine the value of \ Find.
Ans: Given: \ is a right triangle, right-angled at \ we can say that \ bisects the angle \ As \ According to the angle bisector theorem: ABBC=ADDCSubstitute \ and \\\\\
Q.3. In a pyramid, line segment \ is the perpendicular bisector of triangle \ on line segment \ If \ feet and \ feet, find the length of the side \
Ans: Given: \ is the perpendicular bisector on the line segment \By Perpendicular bisector theorem, any point on line segment \ is at an equal distance from points \ and \Therefore, \From the figure, \ feet.So, \ feet.
Q.4. In \ if \ bisects \ Find the value of \?
Ans: Given that, \ is the bisector of \According to the angle bisector theorem: \\\\\\
Q.5. Here, \ Find \ and the length of each segment.
Ans: Given:By using the Perpendicular bisector theorem \\\\So, the values of \ is 8the sides \ and \
Proof Of Angle Bisector Theorem
We can easily prove the angle bisector theorem, by using trigonometry here. In triangles ABD and ACD using the law of sines, we can write
\ .
\ .
The angles ADC and BDA make a linear pair and hence called adjacent supplementary angles.
Since the sine of supplementary angles are equal, therefore,
Sin BDA = Sin ADC ..
Also,
DAC = BAD
Thus,
Sin BDA = Sin ADC
Hence, from equations 3 and 4, we can say, the RHS of equations 1 and 2 are equal, therefore, LHS will also be equal.
Hence, the angle bisector theorem is proved.
Condition:
If the angles DAC and BAD are not equal, the equation 1 and equation 2 can be written as:
\ sin BAD = sin BDA
\ sin DAC = sin ADC
Angles ADC and BDA are supplementary, hence the RHS of the equations are still equal. Hence, we get
\ sin BAD = \ sin DAC
This rearranges to generalized view of the theorem.
Read Also: Homework 2 Segment Addition Postulate Answer Key
Interior Angle Bisector Theorem
In the triangle ABC, the angle bisector intersects side BC at point D. See the figure below.
As per the Angle bisector theorem, the ratio of the line segmentBD to DC equals the ratio of the length of the side AB to AC.
Conversely, when a point D on the side BC divides BC in a ratio similar to the sides AC and AB, then the angle bisectorof A is AD. Hence, according to the theorem, if D lies on the side BC, then,
If D is external to the side BC, directed angles and directed line segments are required to be applied in the calculation.
Angle bisector theorem is applied when side lengths and angle bisectors are known.
Theorems On Internal And External Angle Bisectors Of A Triangle
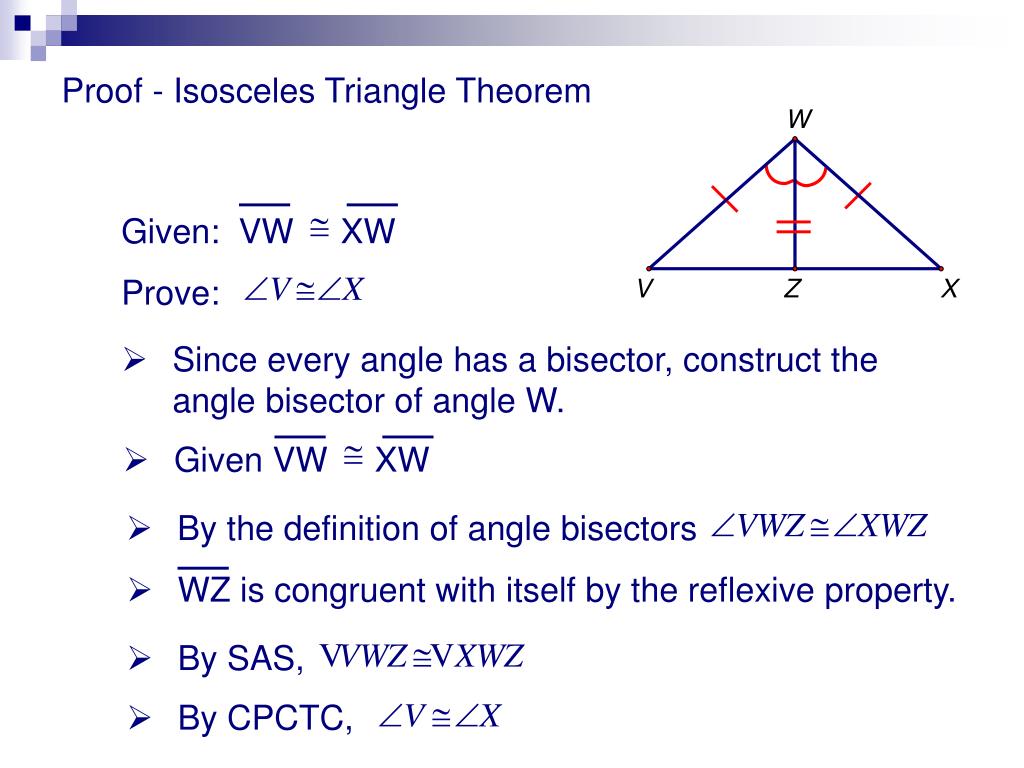
In the below two theorems, we will learn that the internal bisector angle of a triangle divides the opposite side in the ratio of the sides containing the angle and vice-versa.
Theorem 1: The internal angle bisector of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
Given: In \ is the internal bisector of \ and meets \ in \.
To prove: \
Construction: Draw \ to meet \ produced to \.
Proof: \ and \ cuts them.
Therefore, \\) and \\) But, \ is the bisector of \)From \\) and \\), we get\
Thus, in \ we have\\\)
Hence, proved.
Theorem 2: In a triangle \, if \ is a point on \ such that \, then \ is the bisector of \.
Given: In \, in which \ is a point on \ such that, \
Construction: Produce \ to \ such that \. Join \.
Proof: In \, we have\ \\)
Now, \\
Thus, in \, we have
Therefore, by the converse of the Basic proportionality theorem, we have\\\)
and, \\)
But, \ from \\)\
Hence, \ is the bisector of \.
In the following theorem, we shall prove that the bisector of the exterior of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle.
Theorem 3: The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle.
Given: In \ is the bisector of exterior angle \ and intersects \ produced in \
To prove: \
Construction: Draw \ meeting \ in \.
Proof: Since \ and \ intersects them.
Hence, proved.
You May Like: Child Of Rage Documentary Beth Thomas
External Angle Bisector Theorem
The external angle bisector of a triangle divides the opposite side externally in the ratio of the sides containing the angle. This condition usually occurs in non-equilateral triangles.
In the triangle \ is the internal bisector of \ which meets \ at \
According to the angle bisector theorem, the ratio of the line segment \ to \ equals the ratio of the length of the side \ to \
Draw a line \ from point \ parallel to \
Here, our given triangle is \ and \ is the external angle bisector of \
\ is drawn parallel to \ such that it intersects the line \ of a triangle at \
From the figure,\ and \ is transversal, and we know that alternate interior angles formed by a transversal are equal.
\ \\)
Similarly, \ and \ is transversal. We have\\) \\)
Given, \ is the angle bisector of \\\)
From \, \) and \,\) we have \
Hence, \ is an isosceles triangle.
So, in \ we have \
According to the basic proportionality theorem, if a line is drawn parallel to one side of the triangle, then it divides the other two sides in the same ratio.Now, in \ we have, \.
So, \
\ Since, \)
Hence, proved.
Construction Of The Angle Bisector
The angle bisector of an angle is one of the most common and elementary point loci in geometry. The angle bisector of an angle is the locus of points equidistant from the sides of the angle. Of course the notion of angle needs to be defined accurately.
Euclid gives the construction in .
1 December 2015, Created with GeoGebra
Let angle be BAC. Euclid picks point D on AB and construct E on AC so that AE = AD. He then forms an equilateral,scalene,isosceles,equilateral triangle DEF and shows that AF is the angle bisector of BAC. As far as logical purity is concerned this is all that is needed to construct a line: the construction is frugally based on the previously established construction and gives exactly what it was set to produce.
The construction presented by the applet is virtually the same, except the common radius of the circles drawn at D and E is no longer required to be DE. The proof is actually the same as before, but the result is more general and better relates to the locus property of the line. I’d say this is a different kind of frugality: getting more for the same effort.
So let AE = AD,AD,DE,BC,BD and circles are drawn centered at D and E and equal radii. The common radius should be chosen so as to make the circles intersect,coincide,exist,intersect. A sure way to achieve this is to choose a radius greater than,greater than,equal to,smaller than AD. Let F be one of the two points of intersection of the circles.
Don’t Miss: What Does Open Sentence Mean In Math
What Is Perpendicular Bisector
A perpendicular bisector is a line segment or a ray or a line which intersects a given line segment at a 90o, and also it passes through the midpoint of the line segment. Two lines are said to be perpendicular to each other when they intersect in such a way that they form 90 degrees with each other. A bisector divides a line into two equal halves. Thus, when we talk about the perpendicular bisector of a line segment AB, it implies:
- It divides AB into two equal halves or bisects it.
- It makes right angles with AB.
- Every point in the perpendicular bisector is equidistant from point A and B.
Introduction To Angle Bisector Theorem
The Angle Bisector Theorem helps to find unknown lengths of sides of triangles because an angle bisector divides the side opposite to that angle into two segments proportional to the triangles other two sides.
You are shining a flashlight and would like to know where the strongest light from the flashlight is. Suppose we view the light as an angle, and the angle bisector of that angle intersects the imaginary other side of our triangle. In that case, the Triangle Angle Bisector Theorem says that the angle bisector divides the opposite side of the triangle in a proportion equal to the proportion of the other two sides.
That means that the strongest light coming from the flashlight will be where the angle bisector intersects the object you are shining the light at. So, the light will be strongest at the angle bisector and slowly lose power as it goes further towards the sides of the triangle.
You May Like: Geometry Dash Hack Tool
How To Construct A Perpendicular Bisector
You will require a ruler and compasses. The steps for the construction of a perpendicular bisector of a line segment are:
- Step 1: Draw a line segment PQ.
- Step 2: Adjust the compass with length a little more than half of the length of PQ.
- Step 3: Place the compass pointer at point P and draw arcs above and below the line.
- Step 4: Keeping the same length in the compass, place the compass pointer at point Q. Similarly, draw two arcs above and below the line keeping the compass pointer at Q.
- Step 5: Mark the points where the opposite arcs cross as X and Y.
- Step 6: Using a ruler, draw a line passing across X and Y.
The perpendicular bisector bisects PQ at a point J, that is, the length PJ is equal to JQ. And the angle between the two lines is 90 degrees.
How To: Bisecting A Given Angle With A Compass And Straightedge
We can bisect any given angle with a compass and straightedge using the following construction:
Lets now see an example of using this construction to correctly identify what a given geometric construction illustrates.
Recommended Reading: I Ready Answers Level E
Lesson Explainer: Geometric Constructions: Angle Bisectors Mathematics
In this explainer, we will learn how to construct angle bisectors using rulers and compasses without protractors.
We first note that bisecting is a common term in geometry, and it means to split into two equal parts . We can extend this idea to trisecting and beyond. Therefore, bisecting an angle means to split the angle into two congruent angles.
We can define this formally as follows.
Properties Of An Angle Bisector
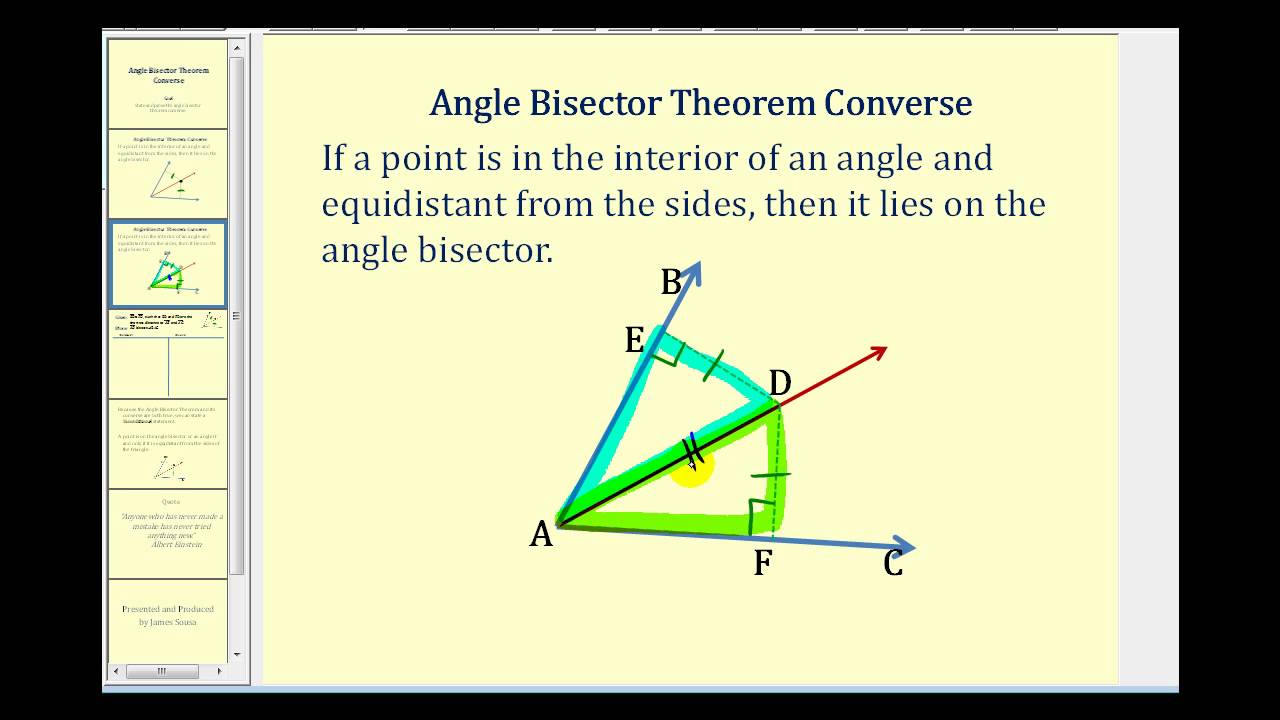
Till now you must be clear about the meaning of angle bisector in geometry. Now, let us learn some of the angle bisector properties listed below:
- An angle bisector divides an angle into two equal parts.
- Any point on the bisector of an angle is equidistant from the sides or arms of the angle.
- In a triangle, it divides the opposite side into the ratio of the measure of the other two sides.
Recommended Reading: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
Construction Of Bisector Of A Given Angle
To draw a ray \ bisecting a given angle \, follow the below steps.
Verification: Measure \ and \. We will find that \.