Algebra Operations With Radical Expressions

Multiply Radicals With Multiple Terms

When multiplying multiple term radical expressions it is important to follow the Distributive Property of Multiplication, as when you are multiplying regular, non-radical expressions.

Radicals follow the same mathematical rules that other real numbers do. So, although the expression \sqrt may look different than a, you can treat them the same way.

Lets have a look at how to apply the Distributive Property. First lets do a problem with the variable a, and then solve the same problem replacing a with \sqrt.

Simplifying Square Root Expressions Khan Academy Help Center

Posted: May 07, 2017 ·Khan Academy, in the steps, just adds the z’s, turning out as z^5. Why is it not z^6? If you are multiplying everything in the radical, then why would you not do the same to everything under the radical? Does this make sense? I also have one more question: would a^8=a^4? In other words, would the square root of a^8 simplify to just a^4?

Algebra 2 Operations With Radical Expressions Worksheet Answers

Algebra 2 Operations With Radical Expressions Worksheet Answers It is actually tedious whenever your kids request you in helping these algebra house functions, and also you are not able to do this residence operates, or you do not find out about them in which you have not completed algebra inside your higher school days and nights. This sort of circumstance is very hectic and through the help of some excellent Algebra helping aids as well as your youngsters are well-ready for coming test. At this point, the net will help to take care of your issue you can find a wide range of Algebra 2 Operations With Radical Expressions Worksheet Answers and some other resources on the net, which helps the hard understanding process. Nevertheless, these algebra equipment are a fun way to enhance your math talent and some practice will give more advantages in upcoming math examination. These worksheets consist of thousands of difficulties and equations where you can check yourself. And you may find an respond to crucial for those these complications in this web site.

Also Check: Geometry Dash 1 20

I Can Divide Radical Expressions And Rationalize A Denominator

Algebra 2 operations with radical expressions worksheet. Simplifying Radical Expressions Calculator. Function Operations And Compositions Coloring Activity Teaching Algebra Algebra Lesson Plans Algebra Lessons. Please view the preview to ensure this product is appropriate for your classroom.

1 5 3 3 3 2 2 8 8 3 4 6 6 4 3 5 2 5 5 3 27 3 27 3 27 6 3 12 3 3 3 20 7 2 45 3 20 2 6 8 3 6 3 2 6. ALL POSSIBLE SOLUTIONS IN THE ORIGINAL EQUATION TO BE CERTAIN THEY. Program could freeze.

This last main operation can be described with words such as. 2 2 3x 2x 5 2 You must FOIL on the right 3x 2×52 2×52 3 2 5 2 2 52 2 54 2 x x x x Combine both radicals in the middle. Multiplying Radical Expressions Worksheets These Radical Worksheets will produce problems for multiplying radical expressions.

Order of operations evaluating expressions number sets adding rational numbers. This clip includes some subtitles to help you along. Remember to check for extraneous solutions.

The preview shows the entire maze. Multiply by a form of 1 to get it out. 3 Take the quiz.

A worksheet is helpful for additional practice after you have learned the concepts. Free Algebra 2 worksheets created with Infinite Algebra 2. Function Operations could have Illegal Expression as an answer or as a choice.

Algebra 2 worksheets general functions worksheets. OPERATIONS WITH RADICALS2It is not appropriate to leave a radical in the denominator of a fraction. Get the best learning program for your family.

The Learning Outcomes For This Lesson Include:

• Multiply and divide radical expressions
• Use the product raised to a power rule to multiply radical expressions
• Use the quotient raised to a power rule to divide radical expressions
• Determine when two radicals have the same index and radicand
• Recognize when a radical expression can be simplified either before or after addition or subtraction
• Use the distributive property to multiply multiple term radicals
• Use the power of a product rule to simplify products of multiple term
• Define and recognize a rational number
• Rationalize denominators with one or multiple terms

Read Also: Monitoring Progress And Modeling With Mathematics Geometry Answers

Rational Expressions And Equations

Posted: In this video, Salman Khan of Khan Academy shows you how to simplify radicals or square roots. … so you can be successful when you take on high-school Math & Algebra. The Princeton Review. Algebra I: More Rational Expressions This video includes sample problems and step-by-step explanations of simplifying rational expressions for the …

Courses142View detail Preview site

Rationalizing The Denominator With Higher Roots

When we rationalized a square root, we multiplied the numerator and denominator by a square root that would give us a perfect square under the radical in the denominator. When we took the square root, the denominator no longer had a radical.

We will follow a similar process to rationalize higher roots. To rationalize a denominator with a higher index radical, we multiply the numerator and denominator by a radical that would give us a radicand that is a perfect power of the index. When we simplify the new radical, the denominator will no longer have a radical.

For example,

Don’t Miss: What Are 4 Goals Of Psychology

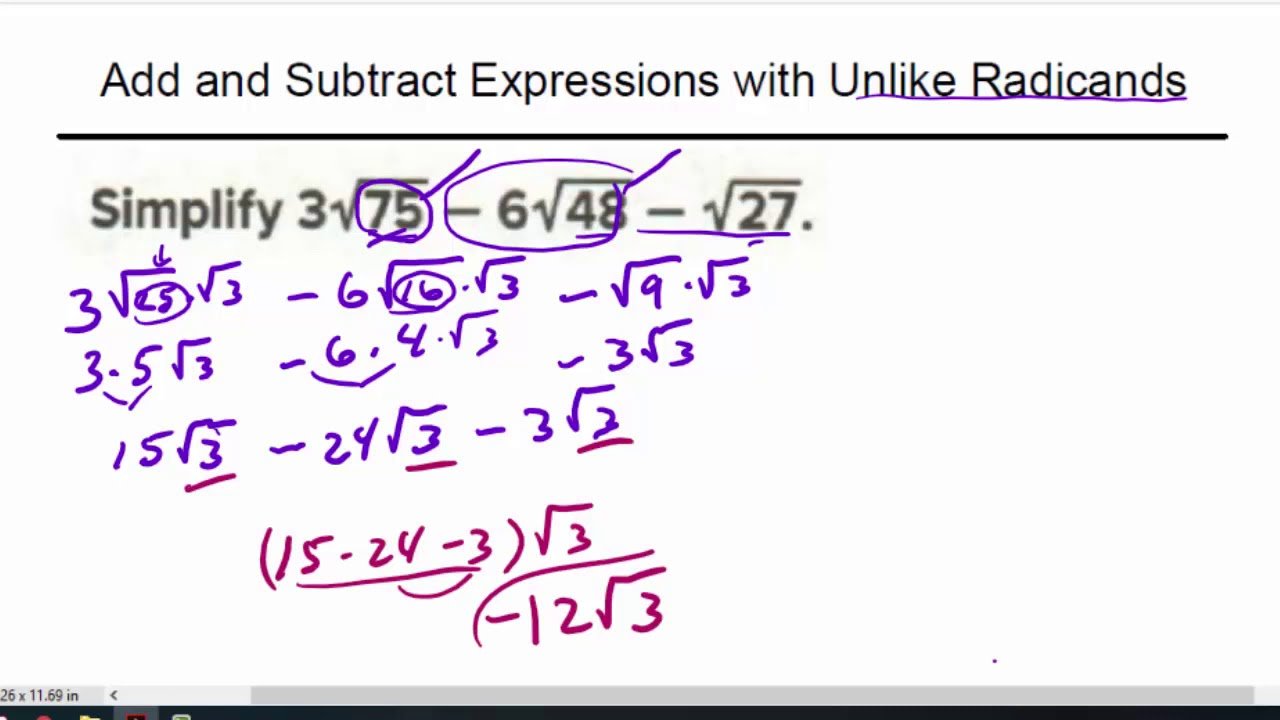
Add And Subtract Radical Expressions

Adding and subtracting radicals is much like combining like terms with variables. We can add and subtract expressions with variables like this:

5x+3y – 4x+7y=x+10y

There are two keys to combining radicals by addition or subtraction: look at the index, and look at the radicand. If these are the same, then addition and subtraction are possible. If not, then you cannot combine the two radicals.

Keys

Remember the index is the degree of the root and the radicand is the term or expression under the radical. In the diagram below, the index is n, and the radicand is 100. The radicand is placed under the root symbol and the index is placed outside the root symbol to the left:

Index and radicand

Practice identifying radicals that are compatible for addition and subtraction by looking at the index and radicand of the roots in the following example.

Simplifying Expressions With Higher Roots

Posted: n is called the index of the radical. We do not write the index for a square root. Just like we use the word cubed for b3 b 3, we use the term cube root for 3a a 3. We refer to the figure above to help us find higher roots. 43 = 64 364 = 4 34 = 81 481 = 3 5 = 32 532 = 2 4 3 = 64 64 3 = 4 3 4 = 81 81 4 = 3 …

Courses362View detail Preview site

Also Check: Beth Thomas Brother Now

Radical Expressions And Equations Unit Test Answers

Posted: Expressions Adding, Subtracting, Multiplying, Dividing, \u0026 Rationalize Simplifying Rational Expressions Simplify a radical expression with variables Solving Radical Equations Restrictions on Radical Expressions Pre-Calculus 11 Simplifying Complex Rational Expressions Radical expressions with higher roots | Algebra I | Khan …

Courses391View detail Preview site

Rationalizing Denominators With One Term

Lets start with the fraction \displaystyle \frac}. Its denominator is \sqrt, an irrational number. This makes it difficult to figure out what the value of \displaystyle \frac} is.

You can rename this fraction without changing its value, if you multiply it by 1. In this case, set 1 equal to \displaystyle \frac}}. Watch what happens.

\displaystyle \frac}\cdot 1=\frac}\cdot \frac}}=\frac}}=\frac}}=\frac}

The denominator of the new fraction is no longer a radical .

So why choose to multiply \displaystyle \frac} by \displaystyle \frac}}? You knew that the square root of a number times itself will be a whole number. In algebraic terms, this idea is represented by \sqrt\cdot \sqrt=x. Look back to the denominators in the multiplication of \displaystyle \frac}\cdot 1. Do you see where \sqrt\cdot \sqrt=\sqrt=2?

In the following videos we show examples of rationalizing the denominator of a radical expression that contains integer radicands.

Here are some more examples. Notice how the value of the fraction is not changed at allit is simply being multiplied by another name for 1.

Read Also: How To Calculate The Percent Error In Chemistry

Simplificao De Razes Com Ndices De

Posted: RKA – Até agora, ao lidar com radicais, usamos apenas a raiz quadrada. Vimos que, se eu escrever um sinal radical assim e colocar um 9 sob ele, isso significa a raiz quadrada positiva de 9, que é +3. Ou podemos ver como a raiz quadrada positiva de 9. Agora, o que está implícito quando escrevemos assim é que extraí a raiz quadrada.

Courses358View detail Preview site

Algebra 12 2 Operations With Radical Expressions Review

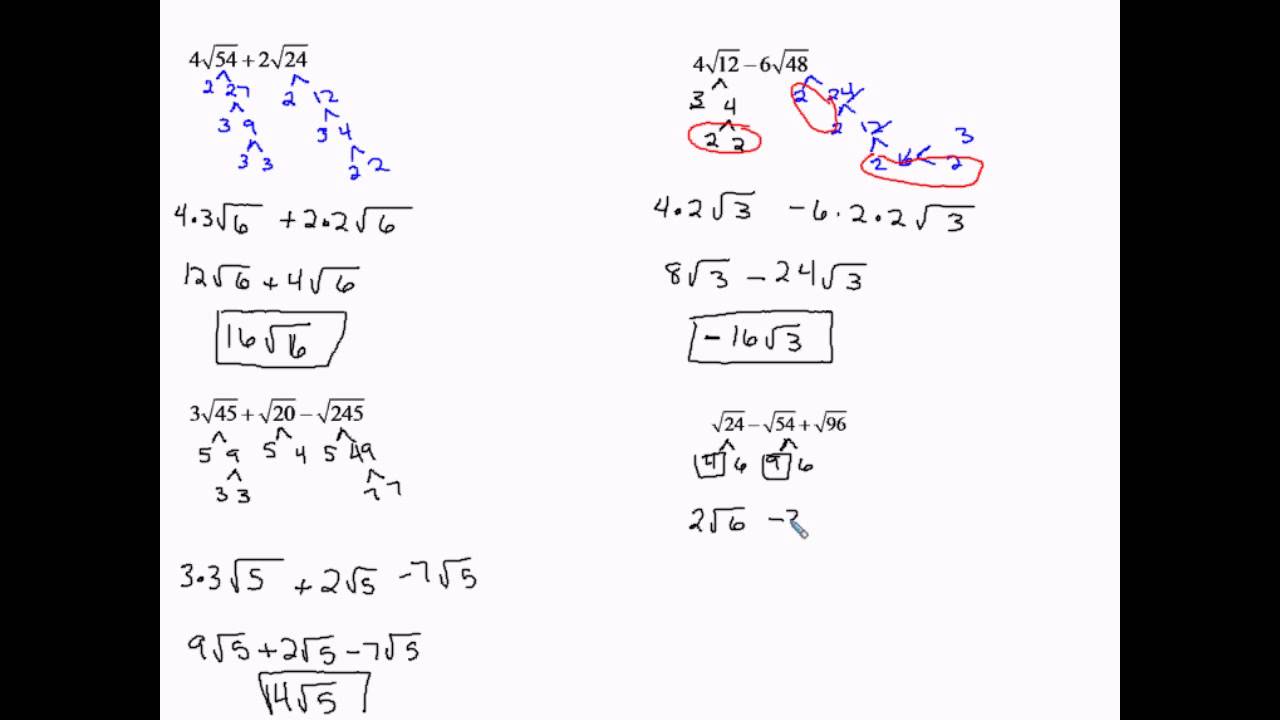
• Slides: 15

Algebra 12. 2 Operations with Radical Expressions

Review: Simplifying Expressions Prime factorization can be useful 1. Factor terms under the radical. Find the largest perfect square factor. Take square roots outside. 2. Rewrite in simplified form.

Warm-Up: You try.

Adding and Subtracting Radicals You can add and subtract terms that have the same radicand. These are LIKE TERMS.

Add and Subtract: You try. Simplify each radical term first

Add and Subtract: Simplify each term first.

Multiplying Radicals 1. Multiply terms outside the radical together. 2. Multiply terms inside the radical together. 3. Simplify.

Multiplying Radicals You can multiply using distributive property and FOIL. Its a DTS!

Multiply: You try. Its a PST!

Dividing to Simplify Radicals No radicals in the denominator allowed Denominators must be rationalized. Multiply by 1 in the form of 3 1

Using the Conjugate to Simplify Conjugate Expression The other part of a DTS Conjugate Product The radical goes away every time

Dividing to Simplify Radicals Multiply by 5 1 11 1 in the form of conjugate

Simplify: You try.

Summary: To ADD and SUBTRACT To MULTIPLY COMBINE LIKE TERMS Outside NUMBERS x NUMBERS Inside NUMBERS x NUMBERS DISTRIBUTE and FOIL To DIVIDE Rationalize denominator using 1 Use conjugate ALWAYS SIMPLIFY AT THE END IF YOU CAN

Homework pg. 719 #5 -11 odd #19 -49 odd

You May Like: Algebra And Trigonometry 4th Edition Stewart Pdf Free

Basic Rule On How To Multiply Radical Expressions

A radicand is a term inside the square root. We multiply radicals by multiplying their radicands together while keeping their product under the same radical symbol. What happens then if the radical expressions have numbers that are located outside?

We just need to tweak the formula above. But the key idea is that the product of numbers located outside the radical symbols remains outside as well.

Lets go over some examples to see how these two basic rules are applied.

Multiplying And Dividing Radicals

Whenever we have two or more radical terms which are multiplied with same index, then we can put only one radical and multiply the terms inside the radical.

Whenever we have two or more radical terms which are dividing with same index, then we can put only one radical and divide the terms inside the radical.

Problem 1 :

Simplify the following radical expression

730 + 275 + 550

Solution :

= 7 30 + 2 75 + 5 50

First we have to split the given numbers inside the radical as much as possible.

= + +

Here we have to keep 30 as it is.

= 30 + 5 3 + 5 2

Problem 2 :

Simplify the following 5 x 18

Solution :

According to the laws of radical,

= ==> ==> 3 5

Problem 3 :

You May Like: Common Core Worksheets 2nd Grade

Multiply Binomial Expressions That Contain Radicals

You can use the same technique for multiplying binomials to multiply binomial expressions with radicals.

As a refresher, here is the process for multiplying two binomials. If you like using the expression FOIL to help you figure out the order in which the terms should be multiplied, you can use it here, too.

Operations On Radical Expressions

• Multiply and divide radical expressions
• Use properties of exponents to multiply and divide radical expressions

Multiply and Divide

You can do more than just simplify radical expressions. You can multiply and divide them, too. Multiplying radicals is very simple if the index on all the radicals match. The prodcut rule of radicals can be generalized as follows

Also Check: Lewis Structure Of Ccl4

Rational Exponents And Radicals

Posted: The Rational exponents and radicals exercise appears under the Algebra I Math Mission. This exercise practices evaluating numerical expressions with rational exponents, and convert between equivalent forms of exponential and radical expressions. There are two types of problem in this exercise: Find the value of the variable: This problem has a numerical

Courses132View detail Preview site

Khan Academy Simplify Radical Expressions

Posted: Simplifying radical expressions – Khan Posted: Oct 02, 2016 · Simplifying radical expressions: two variables Our mission is to provide a free, world-class education to anyone, anywhere. Khan Academy is a 501 nonprofit organization. Author: Sal Khan,Monterey Institute for Technology and Education Courses

Courses406View detail Preview site

You May Like: Who’s Khloe Kardashian’s Real Dad

A Product Raised To A Power Rule

For any numbers a and b and any integer x: ^}=^}\cdot ^}

For any numbers a and b and any positive integer x: ^}}=^}}\cdot ^}}

For any numbers a and b and any positive integer x: \sqrt=\sqrt\cdot \sqrt

The Product Raised to a Power Rule is important because you can use it to multiply radical expressions. Note that the roots are the sameyou can combine square roots with square roots, or cube roots with cube roots, for example. But you cant multiply a square root and a cube root using this rule.

In the following example, we multiply two square roots

Higher Roots Elementary Algebra

Posted: We will now extend the definition to higher roots. n th Root of a Number. If , then is an nth root of a number . The principal n th root of is written . n is called the index of the radical. We do not write the index for a square root. Just like we use the word cubed for ,

Courses322View detail Preview site

Read Also: Holt Mcdougal Geometry Practice Workbook Answers

Operations With Radical Expressions

How Do You Add Radicals with Like Radicands?

Adding radicals isn’t too difficult. As long as they have like radicands, you can just treat them as if they were variables and combine like ones together! This tutorial takes you through the steps of adding radicals with like radicands. Take a look!

How Do You Subtract Radicals with Like Radicands?

Subtracting radicals can be easier than you may think! As long as they have like radicands, you can just treat them as if they were variables and combine like ones together! This tutorial takes you through the steps of subracting radicals with like radicands. Check it out!

How Do You Subtract Radicals with Unlike Radicands?

Subtracting radicals isn’t too hard. Just treat them as if they were variables and combine like ones together! Don’t see like radicals? You may need to simplify the radicals so you can identify similar ones. This tutorial takes you through the steps of subtracting radicals that must first be simplified. Take a look!

Introduction: Algebraic Operations With Radical Expressions

When you learned how to solve linear equations, you probably learned about like terms first. We can only combine terms that are alike, otherwise the terms will lose their meaning. When you learn how to perform algebraic operations on radical expressions in this section you will use the concept of like terms in a new way.

You will also use the distributive property, rules for exponents, and methods for multiplying binomials to perform algebraic operations on radical expressions.

Don’t Miss: Similar Math Definition

Rationalizing Denominators With Two Terms

Denominators do not always contain just one term, as shown in the previous examples. Sometimes, you will see expressions like \displaystyle \frac+3} where the denominator is composed of two terms, \sqrt and +3.

Unfortunately, you cannot rationalize these denominators the same way you rationalize single-term denominators. If you multiply \sqrt+3 by \sqrt, you get 2+3\sqrt. The original \sqrt is gone, but now the quantity 3\sqrt has appearedthis is no better!

In order to rationalize this denominator, you want to square the radical term and somehow prevent the integer term from being multiplied by a radical. Is this possible?

It is possibleand you have already seen how to do it!

Recall that when binomials of the form are multiplied, the product is . So, for example, =^}-3x+3x-9=^}-9 notice that the terms 3x and +3x combine to 0. Now for the connection to rationalizing denominators: what if you replaced x with \sqrt?

Look at the side by side examples below. Just as -3x+3x combines to 0 on the left, -3\sqrt+3\sqrt combines to 0 on the right.

There you have it! Multiplying \sqrt+3 by \sqrt-3 removed one radical without adding another.

Rationalize the denominator and simplify.

\displaystyle \frac}+2}

\displaystyle \begin\frac}+2}\cdot \frac-2}-2}\\\\\frac\left}+2 \right)\left}\end

\displaystyle \frac\cdot \sqrt-2\sqrt}\cdot \sqrt-2\sqrt+2\sqrt-2\cdot 2}

Answer

Analysis Of The Solution

Even though our answer contained a variable with an odd exponent that was simplified from an even indexed root, we dont need to write our answer with absolute value because we specified before we simplified that x\ge 0. It is important to read the problem very well when you are doing math. Even the smallest statement like x\ge 0 can influence the way you write your answer.

In our next example we will multiply two cube roots.

Don’t Miss: Algebra 2 Unit Test Edgenuity

A Quotient Raised To A Power Rule

For any real numbers a and b and any positive integer x: \displaystyle \right)}^}}=\frac^}}}^}}}

For any real numbers a and b and any positive integer x: \displaystyle \sqrt}=\frac}}

As you did with multiplication, you will start with some examples featuring integers before moving on to more complex expressions like \displaystyle \frac^}}}}.