Algebra 2 Absolute Value Functions And Graphs

Identifying Parts Of An Absolute Value Function

Thanks, ***** ***** screenshot of full page.

okay

for a function f = a| x – h| + k

when x > h, slope m = a on the right side of the vertex and when x < h, slope m is – a on the left side of the vertex.

If the slope is between 1 and 0, the opening is wider than the parent graph. If the slope, or a, is greater than 1, then that opening is narrower.

To find the y-intercept, put x = 0 and solve for y that value of y will be the y-intercept.

In the function f = a| x – h| + k

Put x = 0

f = a|0-h| + k = ah + k

y-intercept is .

vertex form is f = a|x – h| + k

vertex is

Axis of symmetry is x=h.

Curve opens up if a> 0 and opens down if a< 0.

curve is wider than the graph of y=|x| if |a|< 1 and narrower if |a|> 1.

Please rate and feel free to request for next questions.

Thanks

Absolute Value Function Definition

The absolute value function is defined as an algebraic expression in absolute bar symbols. Such functions are commonly used to find distance between two points. Some of the examples of absolute value functions are:

All the above given absolute value functions have non-negative values, that is, their range is all real numbers except negative numbers. All these functions change their nature after a point. We can find those points by expressing the absolute value function f = a |x – h| + k as,

f = a + k, if 0 and

= a + k, if < 0

Relationship To The Sign Function

The absolute value function of a real number returns its value irrespective of its sign, whereas the sign function returns a number’s sign irrespective of its value. The following equations show the relationship between these two functions:

|

> 0. }=}=-1& x< 0\\1& x> 0.\end}}

The real absolute value function is an example of a continuous function that achieves a global minimum where the derivative does not exist.

The subdifferential of |x| at x = 0 is the interval .

The complex absolute value function is continuous everywhere but complex differentiablenowhere because it violates the CauchyRiemann equations.

The second derivative of |x| with respect to x is zero everywhere except zero, where it does not exist. As a generalised function, the second derivative may be taken as two times the Dirac delta function.

The antiderivative of the real absolute value function is

, }+C,}

where C is an arbitrary constant of integration. This is not a complex antiderivative because complex antiderivatives can only exist for complex-differentiable functions, which the complex absolute value function is not.

The standard Euclidean distance between two points

a

2 . -b_)^+^}}=^^}}.}

The above shows that the “absolute value”-distance, for real and complex numbers, agrees with the standard Euclidean distance, which they inherit as a result of considering them as one and two-dimensional Euclidean spaces, respectively.

d

< 0. a,& }a\geq 0\\-a,& }a< 0.\end}\right.}

v

Recommended Reading: What Is Meant By Extrapolation In Chemistry

Analysis Of The Solution

Note that these equations are algebraically equivalentthe stretch for an absolute value function can be written interchangeably as a vertical or horizontal stretch or compression.

Q & A

If we couldnt observe the stretch of the function from the graphs, could we algebraically determine it?

Yes. If we are unable to determine the stretch based on the width of the graph, we can solve for the stretch factor by putting in a known pair of values for

Now substituting in the point

Graphing Absolute Value Functions

In this section, we will learn graphing absolute value functions of the form f = a |x – h| + k. The graph of an absolute value function is always either ‘V-shaped or inverted ‘V-shaped depending upon the value of ‘a’ and the gives the vertex of the graph. Let us plot the graph of two absolute value functions below.

f = 2 |x + 2| + 1 and g = -2 |x – 2| + 3

On comparing the two absolute value functions with the general form, a is positive in f, so it will open upwards and its vertex is . For g, the value of a = -2 which is negative, so the graph will open downwards and its vertex is . The image below shows the graph of the absolute value functions f and g.

Important Notes on Absolute Value Function

• The general form of the absolute value function is f = a |x – h| + k, where is the vertex of the graph.
• An absolute value function is a function in algebra where the variable is inside the absolute value bars.
• The graph of an absolute value function is always either ‘V-shaped or inverted ‘V-shaped depending upon the value of ‘a’.

Related Articles:

Recommended Reading: What Is Sexual Selection In Biology

Example : Finding The Range Of An Absolute Value Function Using A Graph

Find the range of the function

We can see that the graph has a vertex at ( , a line of symmetry of -intercept of 2. By inputting values of and observing the resulting outputs, we can confirm the graphs validity.

Lets use the graph to help determine the domain and range of ) . Recall that the domain of a function is the set of all possible input values, while the range is the set of all possible output values. Another way to say this is that the domain is all possible values of the independent variable, while the range is all possible values of the dependent variable.

The arrows tell us that the graph extends infinitely to both the left and the right, so we know that the domain must be the set of all real numbers, or . The arrows also tell us that the graph extends infinitely upward, but we can see that it lies only on or above the -axis. In other words,the smallest value of is 0, but there is no largest value. Thus, we know that the range is

Need Help Graphing An Absolute Value Function

The function I have is $$|x-1|+|y+2|\leq2$$

So I tried graphing it the same way I would $|x|+|y|\leq1$

I know that $|x-1|$ is $x-1$ when $x> 0$ and $-x+1$ when $x< 0$

Similarly, I know that $|y+2|$ is $y+2$ when $y> 0$ and $-y-2$ when $y< 0$

So, I have four cases:

I. $x> 0,y> 0$

II. $x< 0,y> 0$

III. $x< 0,y< 0$

IV. $x> 0,y< 0$

So for Quadrant I, we need to solve $x-1+y+2\leq2$ and get $y\leq-x+1$

Quadrant II, we solve $-x+1+y+2\leq2$ and get $y\leq x-1$

Quadrant III, we solve $-x+1-y-2\leq2$ and get $y\geq -x-3$

Quadrant IV, we solve $x-1-y-2\leq2$ and get $y\geq x-5$

When I graph these lines in their respective quadrants, I do not get the correct answer. Can someone please tell me where I went wrong in my method?

Read Also: What Is C In Physics

Cite This Page As Follows:

“How to graph absolute value functions?” eNotes Editorial, 23 July 2020, https://www.enotes.com/homework-help/how-to-graph-absolute-value-functions-2371245.Accessed 21 Oct. 2022.

Who are the experts?Our certified Educators are real professors, teachers, and scholars who use their academic expertise to tackle your toughest questions. Educators go through a rigorous application process, and every answer they submit is reviewed by our in-house editorial team.

The absolute value function is defined by `f=|x|=`.

The graph consists of two rays with a common endpoint and opposite slopes. The common endpoint is called the vertex, and the rays are called the sides. The graph forms a V or an inverted V (a typical V reflected over a…

Standard Form And Its Uses:

Don’t Miss: Unit 2 Formative Assessment Common Core Algebra 2

Definition: Transformations Of The Graph Of The Absolute Value Function =

• The graph of is a horizontal translation of the graph of is positive, the translation is is negative, the translation is | units left. The domain and range of are the same as those of
• is a vertical translation of the graph of is positive, the translation is is negative, the translation is | units down. The domain of is the same as that of
• is a vertical stretch of the graph of by a scale factor of | and a vertical compression by a scale factor of | is negative, the graph of is also reflected over the -axis, which means that the graph of will open downward instead of upward.
• The graph of is a horizontal compression of the graph of by a scale factor of 1 and a horizontal stretch by a scale factor of 1 is negative, the graph of is also reflected over the -axis.

Some examples of absolute value functions in various forms and their graphs are in the problems that follow.

Absolute Value Function Examples

Read Also: What Can You Learn In Psychology Class

How Do You Solve Absolute Value Equations And Inequalities

The steps to solve absolute value equations are as follows:

You can solve absolute value inequalities by rewriting them as compound inequalities. Compound inequalities are two inequalities joined together by the words and or or.

For all real numbers a and b, where b 0:

The solution of an inequality can be represented on the number line using an empty circle to represent that the value of x is not part of the solution, and a closed circle if the value of x is part of the solution.

Graphing An Absolute Value Function

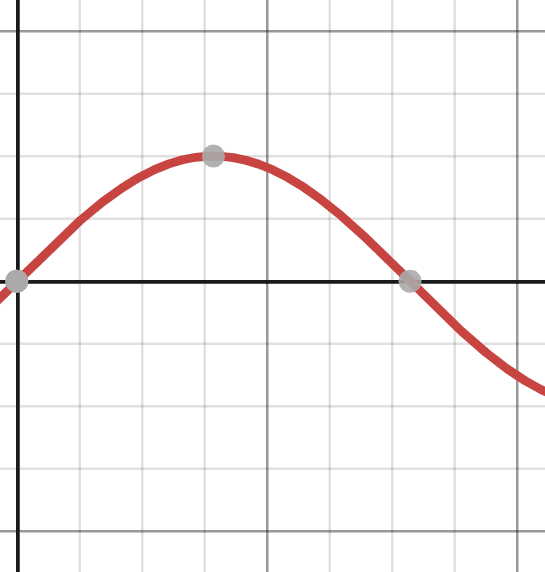
The most significant feature of the absolute value graph is the corner point at which the graph changes direction. This point is shown at the origin in Figure 2.

Figure 3 shows the graph of y x | has been shifted right 3 units, vertically stretched by a factor of 2, and shifted up 4 units. This means that the corner point is located at (

Writing an Equation for an Absolute Value Function Given a Graph

Write an equation for the function graphed in Figure 4.

Solution

The basic absolute value function changes direction at the origin, so this graph has been shifted to the right 3 units and down 2 units from the basic toolkit function. See Figure 5.

We also notice that the graph appears vertically stretched, because the width of the final graph on a horizontal line is not equal to 2 times the vertical distance from the corner to this line, as it would be for an unstretched absolute value function. Instead, the width is equal to 1 times the vertical distance as shown in Figure 6.

From this information we can write the equation

Analysis

Note that these equations are algebraically equivalentâthe stretch for an absolute value function can be written interchangeably as a vertical or horizontal stretch or compression. Note also that if the vertical stretch factor is negative, there is also a reflection about the x-axis.

Read Also: Baldor Algebra Book English Edition

Properties: The Absolute Value Function =

• -intercept: 0

All absolute value functions that have a linear expression within the absolutevalue symbols have graphs that are v-shaped. However, the functions other properties may differ. Transforming the graph of the function | by translating it, stretching or compressing it, or reflecting it across an axis canallow us to more easily sketch the graph of an absolute value function in a differentform so that we can identify the domain and range of the function.

Lesson Explainer: Absolute Value Functions Mathematics

In this explainer, we will learn how to evaluate and graph absolute value functionsand identify their domain and range.

Recall that the absolute value of a real number is its distance from 0on the number line. For example, in the expression | is 5 as well, because 5 is also located 5 units from 0 on the number line.

A distance is never negative, so the absolute value of a number will always be positive or 0. In addition to numbers, we can put algebraic expressions within absolute value symbols to define functions. These types of functions are called absolute value functions.

Don’t Miss: What Is Oscillation In Physics

Absolute Value Functions Real World Applications

As you know Absolute Value is a way to eliminate negative numbers in situations in which they are not called for. For example, if your student walks to school and it is a 2 mile walk we would say he or she walked 2 miles. However, when the student walks home from school that night we would not say it’s a -2 mile walk. For instance, when dealing with direction we can illustrate many of these situations so that the students can have visual aids to prove everything you teach them. Here is an example…

Solving An Absolute Value Equation

In Other Type of Equations, we touched on the concepts of absolute value equations. Now that we understand a little more about their graphs, we can take another look at these types of equations. Now that we can graph an absolute value function, we will learn how to solve an absolute value equation. To solve an equation such as 8

You May Like: How To Find Ksp Chemistry

Properties Of Absolute Values

The properties of absolute values are:

• The absolute value of a number will always give a positive result.

| = 5

• The absolute value of a number x will give the same result as the absolute value of -x.

• The absolute valueof the product of two values a and b can be split into the product of two separate absolute values.

• The absolute valueof the division of two values a and b can be split into the division of two separate absolute values.

• The absolute valueof the sum or subtraction of two values a and b, cannot be split into the sum or subtraction of two separate absolute values.

Absolute value equations are equations that include absolute value expressions in them.

For any real numbers a and b, where b 0:

I < 0

As you can see in the expression above, when solving equations, absolute values involve an extra step. Keeping in mind that the value inside an absolute value could be positive or negative, you need to solve the equation considering both cases, therefore you will get two solutions.

The steps to solve absolute value equations are as follows:

For the equation , we can obtain 2 possible solutions as follows:

1. Solution 1

Solution set:solution set

Absolute Value Equations And Inequalities

Absolute value equations are very useful when dealing with problems involving values that cannot be negative, like distance. For example, imagine that you go to visit your friend Tony who lives on the 4th floor of an apartment block that has 10 floors in total. When you arrive, you cannot remember what floor Tony lives on, so you make your way in, call him from the stairs and ask him what floor he is in. He says he is on the 4th floor, and you say that you are 2 floors away from him. Does that mean that you are on the 2nd floor or on the 6th floor? It could be either because both options are 2 floors away from Tony’s apartment. No matter if you go up or down, the distance is the same.

In terms of absolute value inequalities, they are very handy when calculating margins of error or tolerance, which can be applied, for example, to measurements of weight, length, and temperature in a manufacturing process.

In this article, we will define what absolute value equations and inequalities are, and their rules, and we will also show you how to solve them using practical examples.

The absolute value of a number x is a number with the same magnitude, but positive. Absolute values are generically represented as | | .

But what is the reasoning behind this? This happens because the absolute value represents the distance from zero to a number x on the number line.

The distance from zero to 2 is 2, and the distance from zero to -2 is also 2, therefore |

Evaluate

Recommended Reading: How Do I Learn Physics