Formulas For The Population Standard Deviation
\displaystyle\sigma=\sqrt-\mu)}^}}}}}}}\quad}\sigma=\sqrt-\mu)}}}^}}}}}}}
For the population standard deviation, the denominator is N, the number of items in the population.
In these formulas, f represents the frequency with which a value appears. For example, if a value appears once, f is one. If a value appears three times in the data set or population, f is three.
Five Number Summary And Iqr
The five number summary takes the form: Minimum, \, Median, \, Maximum.
These five values divide the data into quarters: 25% of the data is between the minimum and \, 25% is between \ and the median, 25% is between the median and \, and 25% is between \ and the maximum value.
Moreover, 50% of the data lies between \ and \. The distance between \ and \ is called the interquartile range.
The interquartile range measures the spread in the middle 50% of the data. Subtract \ from \ to find its value.
Examples should help make this clearer.
Example 5
The first 11 days of May 2013 in Flagstaff, AZ, had the following high temperatures shown below. Find the five-number summary and IQR.
| 71 |
To find the five-number summary, you must first order the data from smallest to largest:
57 57 57 57 59 63 65 67 68 69 71
Then find the median. There are \ data values so the median will be a single value in the middle. Here, 63oF is located at the middle of the data set. To find \ and \, look at the numbers in each half on each side of the median. Since 63 is the median, it is not included in either half.
- There are 5 numbers below the median: . The median of these numbers is 57. So, \.
- There are 5 numbers above the median: . The median of these numbers is 68. So, \.
- The minimum is 57°F and the maximum is 71°F.
Thus, the five-number summary is Min = 57°F, Q1 = 57°F, Med = 63°F, Q3 = 68°F, Max = 71°F. The \.
Example 6
The Term Spread Has A Few Meanings To Investors Here’s What You Need To Know
The word “spread” has several different meanings in investing, and can apply to stocks, bonds, or options. Here’s a rundown of the various uses of the term, and how each type of spread can be calculated.
Bid-ask spreadWhen you check a stock quote, in addition to the last trade price, you’ll see two other prices known as the “bid” and the “ask.” The bid price represents the highest price someone is currently willing to pay for the stock, while the ask price represents the lowest price someone is willing to sell the stock for.
Simply put, the difference between the two prices is known as the spread.
In general, larger companies whose stocks have high volumes tend to have low spreads sometimes just a penny or two. On the other hand, stocks of smaller companies with relatively low volume may high much higher spreads.
Yield spreadThe word “spread” is also used when talking about debt securities, such as bonds or CDs. The calculation for a yield spread is essentially the same as for a bid-ask spread simply subtract one yield from the other.
For example, if the market rate for a five-year CD is 5% and the rate for a one-year CD is 2%, the spread is the difference between them, or 3%.
Yield spreads are often expressed in basis points, and a 1% difference in yield is equal to 100 basis points. So, the yield spread between two bonds — one paying 5% and one paying 4.8% could be stated as either 0.2% or 20 basis points.
Also Check: Sketching Functions 1 Algebra With Pizzazz Answers
Which Measure Of Spread Should I Report
The measure of spread to use will depend on which average value you have chosen to report for your dataset. As a general guide:
- If you have reported the mode then you could report the range of the data.
- If you have reported the median then you could report the interquartile range of the data.
- If you have reported the mean then you could report the standard deviation of the data.
Range |
The range of a data set is the difference between the smallest and largest values in the data set. To calculate the range, subtract the smallest number from the largest number . |
|
Example of range by Maths is Fun. The range can be calculated in Excel by taking the difference between the maximum value and the minimum value of the dataset. |
|
Interquartile range |
The interquartile range captures the middle 50% of ordered data. To calculate, order data from smallest to largest. Find the values that are at the first and third quartile . The interquartile range is the difference between the third and first quartile . Note: the second quartile is the median . |
|
Example of interquartile range by Maths is Fun. The interquartile range can be calculated in Excel by taking the difference between the third ) and first ) quartiles. |
|
Standard deviation |
The standard deviation captures on average, how much each data point varies from the mean of the data set. |
|
Example of standard deviation by Maths is Fun. |
Measures Of Location And Spread
May 1, 2022
Year 1: AS Mathematics: Applied: Statistics: Measures of Location and Spread
Lessons on Statistical Sampling
Prerequisite Knowledge
- Use the mode, mean and median to interpret, analyse and compare the distributions of data sets
- Use the range and interquartile range to interpret, analyse and compare the spread of data sets.
Success Criteria
- Calculate measures of location, mean, median and mode
- Recognise when each measure of location is most suitable
- Calculate measures of variation, standard deviation, variance, range and interpercentile range
- Interpret and draw inferences from summary statistics.
Teaching Points
Misconceptions
- When calculating the mean of grouped data, some students may divide by the number of groups rather than the number of data items.
- When finding the standard deviation, students forget to take the square root.
- Some students waste time by ignoring given values and recalculating fx and fx2.
- Students often forget about the effect that coding data has on the variance.
- Students often forget to calculate the mean and standard deviation of grouped data using the statistics mode on their calculator and prefer to work it out
Don’t Miss: What Is Attribution In Psychology
Ks4 Statistics 5 Measures Of Location And Spread
When we talk about measures of location, we are talking about averages, because the average of a data set is effectively a single number that tells us where the data set is located. Measures of spread tell us about how widely the data set is dispersed. These two numbers are the most important statistics in summarising a data set.
There are three averages and one measure of spread that we already know:
1.) The mode: This is the piece of data, or value, that occurs the most frequently
2.) The median: This is the piece of data, or value, that is in the middle if we line all of the data up in order. If there is no value in the middle we take the value that is halfway between the two middle values
3.) The mean: This is the value that we get if we sum the values and then divide our answer by the number of values.
4.) The range: This is.a measure of spread, calculated by subtracting the smallest number from the largest number.
Lets do a short exercise to remind ourselves of these averages :
The solutions are as follows:
Extensionwork
If data is given in the form of a frequency table, we can calculate the mean average using the formula mean = fx / f, where f means the sum of all the frequencies, and fx means the sum of the products of the values with the frequencies. Below is an example of this process:
Try the questions below from exercise 5 on pages 346 to 347 of the extended textbook:
The answers are as follows:
The answers are as follows:
What Are The Measures Of Spread
This post will help you understand the terms involved in describing the measures of spread in Prelim Standard Math. A measure of spread is calculated to determine whether the scores are close together or spread apart. Three measures help us identify these. The range is the difference between the highest score and the lowest score. The interquartile range involves dividing the data into four equal parts and using the interquartile range formula to determine how spread out the data is. Standard deviation is a measure of spread about the mean.
Read Also: Who Uses Math In Their Job
Measures Of Spread And Position
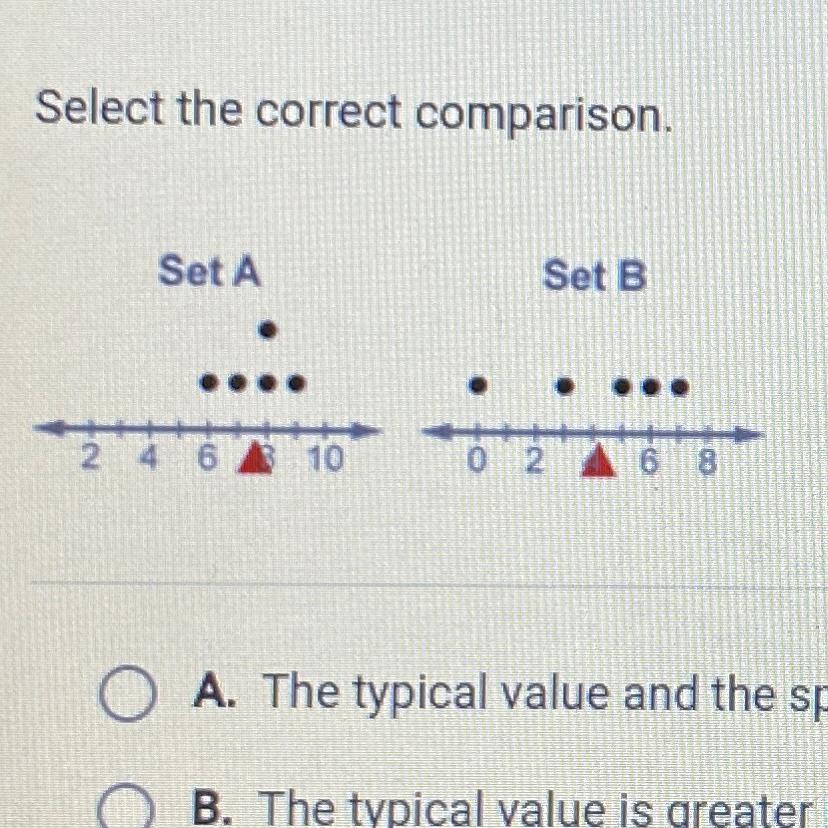
Consider these three sets of student quiz scores on a 10-point quiz:
- Class A: 5, 5, 5, 5, 5, 5, 5, 5, 5, 5
- Class B: 0, 0, 0, 0, 0, 10, 10, 10, 10, 10
- Class C: 4, 4, 4, 5, 5, 5, 5, 6, 6, 6
All these data sets have mean \ and median of 5, yet the three sets of scores are clearly quite different.
In Class A, everyone had the same score. In Class B, half the class got no points and the other half got a perfect score of 10 points. Scores in Class C were not as consistent as those in Class A but also not as widely varied as those in Class B.
This scenario shows that, in addition to the mean and median which measure the “typical” value of a data set, we also need a way to measure how “spread out” or varied each data set is. There are several ways to measure the variation and locate positions in a data distribution. In this section we explore range, standard deviation, percentiles, quartiles, and the interquartile range . We also examine a graphical representation of spread using a box plot.
Finding Descriptive Statistics Using The Ti Calculator
We have already used the TI calculator to find the mean and the median in the previous section. Now, we expand the previous explanation to measures of spread and position. The procedures for finding the descriptive statistics for the Flagstaff, AZ temperature data used in examples throughout this section are shown below.
First, enter the data into the calculator. To do this, press STAT. The STAT button is in the third row of buttons, next to the arrow keys. Once you press STAT, you will see the following screen:
Choose 1:Edit and you will see the following screen. If there is already data in List 1 , then you should move the cursor up to L1 by using the arrow keys. Then, press CLEAR and ENTER. This should clear all data from List 1 .
Now type all of the data into List 1 . Be sure to press ENTER after each value. You can only see the last six data values entered on the screen, but all the data has been entered.
Next, press STAT again and move over to CALC using the right arrow button. You will see the following screen:
Choose 1:1-Var Stats. This will put 1-Var Stats on your home screen. Type the name of the list containing the data L1 , and the calculator will show the following:
At this point press ENTER, and you will see the results. You will need to use the down arrow button to see all of the results.
Therefore, the mean is \, the standard deviation is \, and the five-number summary is Min = 57°F, Q1 = 57°F, Med = Q2 = 63°F, Q3 = 68°F, Max = 71°F.
Don’t Miss: What Is Crystallization In Chemistry
Shape Center And Spread Of A Distribution
A population parameter is a characteristic or measure obtained by using all of the data values in a population.
A sample statistic is a characteristic or measure obtained by using data values from a sample.
The parameters and statistics with which we first concern ourselves attempt to quantify the “center” and “spread” of a data set. Note, there are several different measures of center and several different measures of spread that one can use — one must be careful to use appropriate measures given the shape of the data’s distribution, the presence of extreme values, and the nature and level of the data involved.
As we consider different measures of center and spread, recall that we really want to know about the center and spread of the population in question — but normally only have sample data available to us.
As such, we calculate sample statistics to estimate these population parameters.
For Continuous Iid Random Variables
For nindependent and identically distributed continuous random variablesX1, X2, …, Xn with the cumulative distribution function G and a probability density function g, let T denote the range of them, that is, T= max-min.
The range, T, has the cumulative distribution function
- F . ^g^\,}x.}
Gumbel notes that the “beauty of this formula is completely marred by the facts that, in general, we cannot express G by G, and that the numerical integration is lengthy and tiresome.”:385
If the distribution of each Xi is limited to the right then the asymptotic distribution of the range is equal to the asymptotic distribution of the largest value. For more general distributions the asymptotic distribution can be expressed as a Bessel function.
The mean range is given by
- n G ^x\,}G}
where x is the inverse function. In the case where each of the Xi has a standard normal distribution, the mean range is given by
- ^)^-\Phi ^)\,}x.}
Also Check: Lewis Structures And Molecular Geometry Lab Answers
Sampling Variability Of A Statistic
How much the statistic varies from one sample to another is known as the sampling variability of a statistic. You typically measure the sampling variability of a statistic by its standard error. The standard error of the mean is an example of a standard error. It is a special standard deviation and is known as the standard deviation of the sampling distribution of the mean. You will cover the standard error of the mean when you learn about The Central Limit Theorem . The notation for the standard error of the mean is \displaystyle\frac}}} where is the standard deviation of the population and n is the size of the sample.
The Shape Of A Distribution
We can characterize the shape of a data set by looking at its histogram.
First, if the data values seem to pile up into a single “mound”, we say the distribution is unimodal. If there appear to be two “mounds”, we say the distribution is bimodal. If there are more than two “mounds”, we say the distribution is multimodal.
Second, we focus on whether the distribution is symmetric, or if it has a longer “tail” on one side or another. In the case where there is a longer “tail”, we say the distribution is skewed in the direction of the longer tail. In the case where the longer tail is associated with larger data values, we say the distribution is skewed right or . In the case where the longer tail is associated with smaller values, we say the distribution is skewed left or .
If the distribution is symmetric, we will often need to check if it is roughly bell-shaped, or has a different shape. In the case of a distribution where each rectangle is roughly the same height, we say we have a uniform distribution.
The below graphic gives a few examples of the aforementioned distribution shapes.
Don’t Miss: What Is Rxn In Chemistry
For Discrete Iid Random Variables
For n independent and identically distributed discrete random variables X1, X2, …, Xn with cumulative distribution functionG and probability mass functiong the range of the Xi is the range of a sample of size n from a population with distribution function G. We can assume without loss of generality that the support of each Xi is where N is a positive integer or infinity.
The range has probability mass function
- f
Quartiles And Interquartile Range
Quartiles tell us about the spread of a data set by breaking the data set into quarters, just like the median breaks it in half. For example, consider the marks of the 100 students below, which have been ordered from the lowest to the highest scores, and the quartiles highlighted in red.
| Order | |
| 100th | 85 |
The first quartile lies between the 25th and 26th student’s marks, the second quartile between the 50th and 51st student’s marks, and the third quartile between the 75th and 76th student’s marks. Hence:
First quartile = ÷ 2 = 45Second quartile = ÷ 2 = 58.5Third quartile = ÷ 2 = 71
In the above example, we have an even number of scores . This means that when we calculate the quartiles, we take the sum of the two scores around each quartile and then half them ÷ 2 = 45) . However, if we had an odd number of scores , we would only need to take one score for each quartile . You should recognize that the second quartile is also the median.
Interquartile range = Q3 – Q1= 71 – 45= 26
However, it should be noted that in journals and other publications you will usually see the interquartile range reported as 45 to 71, rather than the calculated range.
A slight variation on this is the semi-interquartile range, which is half the interquartile range = ½ . Hence, for our 100 students, this would be 26 ÷ 2 = 13.
Read Also: How To Find Tension In Physics
Calculating The Standard Deviation
If x is a number, then the difference x mean is called its deviation. In a data set, there are as many deviations as there are items in the data set. The deviations are used to calculate the standard deviation. If the numbers belong to a population, in symbols a deviation is x . For sample data, in symbols a deviation is \displaystyle-\overline}.
The procedure to calculate the standard deviation depends on whether the numbers are the entire population or are data from a sample. The calculations are similar, but not identical. Therefore the symbol used to represent the standard deviation depends on whether it is calculated from a population or a sample. The lower case letter s represents the sample standard deviation and the Greek letter represents the population standard deviation. If the sample has the same characteristics as the population, then s should be a good estimate of .
To calculate the standard deviation, we need to calculate the variance first. Thevariance is the average of the squares of the deviations . The symbol ^2 represents the population variance the population standard deviation is the square root of the population variance. The symbol s^2 represents the sample variance the sample standard deviation s is the square root of the sample variance. You can think of the standard deviation as a special average of the deviations.
In the following video an example of calculating the variance and standard deviation of a set of data is presented.