Gradualism Vs Punctuated Equilibrium
Punctuated equilibrium is pitted against phyletic gradualism. These competing theories of evolution both hypothesize about the rate of emergence of new species. Gradualism places importance on the slow appearance of new characters in interbreeding subspecies that, over time, lead to the evolution of a new species from ancestral forms.
Fossils seem to appear suddenly throughout history. Punctuated equilibrium tries to explain these fossil gaps or the absence of intermediate forms, by stating that they exist for very short periods of time when speciation occurs intensely in an isolated population.
The criticism of punctuated equilibrium focuses on the possibility that fossil records may simply be incomplete. Intermediate forms may be found in regions where fossils are abundant and well-preserved. In addition, critics point to the fact that there is no evidence that an external homogenizing influence keeps interbreeding populations in stasis.
What Is Static Equilibrium
The static equilibrium is a physical state in which an object is at rest with no net force and no net torque acting on it. Thus for static equilibrium, the object must be in translational equilibrium as well as in rotational equilibrium and another vital condition is that the object must be at rest.
The conditions required for the static equilibrium are as follows:-
1] The object must be in translational equilibrium:-
It means that the net force acting on an object must be equal to zero.
`\sum \vec` = 0
Where `\sum \vec` is the vector summation of all the forces acting onto the object.
In scalar form, the condition becomes,
`\sum F_` = 0`\sum F_` = 0`\sum F_` = 0
Each of the above equations indicates that the sum of the forces in each of the three directions must be equal to zero.
2] The object must be in rotational equilibrium:-
It means that the net torque acting on the object must be equal to zero.
`\sum \vec` = 0
Where `\sum \vec` is the vector summation of the torques acting onto the object.
In scalar form, the condition becomes,
`\sum T_` = 0`\sum T_` = 0`\sum T_` = 0
Each of the above equations indicates that the sum of the torques in each of the three directions must be equal to zero.
3] The object must be at rest:-
The object under static equilibrium must be in a resting condition and it should not move or tilt.
Thus the object must have zero angular velocity and zero translational velocity.
v = 0, `\omega` = 0
`\mathbf}}` = 0, `\mathbf}}` = 0
`\mathbf}` = 0
Examples Of Chemical Equilibrium
There are many examples of systems at equilibrium. We’re going to focus on three in particular:
-
Methanol production
-
Ammonia production
But before we dive into these processes, you need to understand compromise conditions.
Compromise conditions are conditions that dont necessarily give the greatest yield of the product, but are the most economical when it comes to balancing factors like cost and rate of reaction.
Take our general reaction involving A, B, C, and D again. We want to maximise our yield of C and D. Let’s say that the forward reaction is exothermic. According to Le Châtelier’s principle, this means that lowering the temperature increases the rate of the forward reaction – the system will favour the exothermic reaction in order to try and produce extra heat. This will therefore increase our yield of C and D.
However, reducing the temperature slows down the overall rate of reaction and therefore reduces our yield. Whilst a low temperature might produce a lot of C and D, high temperature results in an overall faster rate of reaction. A medium temperature is used instead. This takes both yield and rate of reaction into consideration and in fact gives us more of C and D than a low temperature – simply because the rate of reaction is higher. This is an example of a compromise condition.
Now let’s look specifically at the examples mentioned above.
Recommended Reading: How To Find Force In Physics
What Is Difference Between Steady State And Equilibrium
A steady state is a state where the rate of formation of a species equals the rate of its decomposition in a consecutive reaction. On the other hand, chemical equilibrium is the condition of a reversible reaction taking place where the rate of forward reaction is equal to the rate of backward reaction.
Equilibrium In General Terms
Equilibrium is generally defined as a state of rest, where there is no change. A body at equilibrium will not experience any positive or negative energy transfers. Biology, physics and chemistry define the state of equilibrium in slightly different terms. But the basic premise is the same. A body at equilibrium will have a minimal influence of external forces on it. Even in the presence of external forces, the opposing forces usually have a balanced effect on the object in concern. Objects at equilibrium are distinguished by their stable nature in terms of motion and energy.
Observing things in their state of equilibrium is not a usual sight since they are acted upon by so many forces both internal and external. Gravity and interatomic forces are the most common examples of forces experienced by objects and due to this, they are usually at unrest if not balanced by an equal and opposite force. This need not mean that the two opposing forces should be equal for a body to be in equilibrium. They just need to cancel each other.
Also Check: Whodunnit Algebra 2 Answer Key
What Does Being A Equilibrium Mean
What does being a equilibrium mean? 1 : a state of balance between opposing forces or actions. 2 : the normal balanced state of the body that is maintained by the inner ear and that keeps a person or animal from falling. equilibrium.
What is meaning of equilibrium in chemistry? chemical equilibrium, condition in the course of a reversible chemical reaction in which no net change in the amounts of reactants and products occurs. A reversible chemical reaction is one in which the products, as soon as they are formed, react to produce the original reactants.
What is equilibrium in biology simple definition? Equilibrium is the state in which all forces acting on the body are balanced with an equal and opposite force. An active moving animals condition of bodily balance, in which internal and external forces are in balance. As a result, the system is stable.
Whats an example of equilibrium? A few examples of equilibrium are: A book kept on a table at rest. A car moving with a constant velocity. A chemical reaction where the rates of forward reaction and backward reaction are the same.
Types Of Equilibrium Constant
There are a few different types of equilibrium constant:
Kc
Kc is an equilibrium constant involving concentration. You work with Kc when you have equilibria containing gaseous or aqueous species.
Here’s the equation for Kc. It might look a little complicated – but don’t worry, we’ll talk through it in just a second:
For the reaction ,
What does this all mean? Well, square brackets represent concentration, so eqma means the concentration of A at equilibrium, raised to the power of a. What is a? Take a look at the general equation. a is the molar ratio of A. So if we have two moles of A in the equation, and the equilibrium concentration of A is 0.5 mol dm-3, eqma = 0.52.
To work out Kc, we find a similar value for each of our products and multiply them together. We then find similar values for each of our reactants and multiply them together. We then divide the product value by the reactant value to find Kc.
Here’s an example.
Take the equation E + 2F 2G. Let’s say that at equilibrium, the concentrations of E, F and G are 0.2, 0.3 and 0.4 respectively. Find Kc.
Using the equilibrium concentrations given to us, the equation for Kc looks like this:
Calculating Kc. Anna Brewer, StudySmarter Originals
The units of Kc vary from reaction to reaction. Check out Equilibrium Constants to find out how to work them out. You’ll also find examples of calculating Kc for various different reactions, and the Kc equation for heterogeneous equilibria.
Kp
Kp takes the following equation:
Don’t Miss: What Is Movement In Geography
What Are Gradualism Examples
The definition of gradualism is the slow and gradual changes that happen within an organism or society to make a better environmental fit for animals and humans. An example of gradualism is the stripes of a tiger developing over time so they are better able to hide in tall grass.
How Do You Know If A Population Is In Equilibrium
A population of alleles must meet five rules in order to be considered in equilibrium: 1) No gene mutations may occur and therefore allele changes do not occur. 2) There must be no migration of individuals either into or out of the population. 3) Random mating must occur, meaning individuals mate by chance.
Recommended Reading: Why Are Moles Used In Chemistry
Steady State Vs Equilibrium In Biology
Whether were talking about the concentration of ions in a cell or the internal temperature of a mammal, biological systems tend to remain fairly constant. Unfortunately, few words in biology are as often misused as the family of names related to the balance of a system. Terms like steady state, dynamic equilibrium and chemical equilibrium are sometimes thrown about interchangeably, but these words have very specific technical definitions and they dont mean the same thing.
Minimization Of Gibbs Energy
At equilibrium, at a specified temperature and pressure, and with no external forces, the Gibbs free energyG is at a minimum:
- d
- ^a_N_=b_^}
where aij is the number of atoms of element i in molecule j and b0i is the total number of atoms of element i, which is a constant, since the system is closed. If there are a total of k types of atoms in the system, then there will be k such equations. If ions are involved, an additional row is added to the aij matrix specifying the respective charge on each molecule which will sum to zero.
This is a standard problem in optimisation, known as constrained minimisation. The most common method of solving it is using the method of Lagrange multipliers .
Define:
- i 0 }}}}=\sum _^a_N_-b_^}
This is a set of equations in unknowns and may, therefore, be solved for the equilibrium concentrations Nj as long as the chemical activities are known as functions of the concentrations at the given temperature and pressure. Note that the second equation is just the initial constraints for minimization.
This method of calculating equilibrium chemical concentrations is useful for systems with a large number of different molecules. The use of k atomic element conservation equations for the mass constraint is straightforward, and replaces the use of the stoichiometric coefficient equations. The results are consistent with those specified by chemical equations. For example, if equilibrium is specified by a single chemical equation:,
Recommended Reading: Alphabetical List Of Geometry Terms
What Is Called Diffusion
Diffusion is the movement of a substance from an area of high concentration to an area of lower concentration . Diffusion occurs in liquids and gases when their particles collide randomly and spread out. Diffusion is an important process for living things – it is how substances move in and out of cells.
Modelling Biological Active States As Random Dynamical Attractors
Free energy theorists account of biological systems persistence relies on three main modelling assumptions: 1. ergodicity, 2. the existence of Markov blankets that imply a partition of states into internal and external, 3. the existence of random dynamical attractors.Footnote 8 In this section, we concentrate on assumptions 1 and 3, and on the more fundamental challenge of defining phase spaces for target biological systems in the life sciences.Footnote 9
Don’t Miss: What Is Conscientiousness In Psychology
The Explanatory Scope Of The Fep: A Winged Snowflake
Snowflakes are crystals of ice that grow from droplets of water and water vapour. Given the right temperature and air pressure, an initial few water molecules in a cloud will freeze together in ringed unit cells. As the frozen droplets accumulate water vapour from the surrounding cold air, the molecules of water will get fixed in a crystal with increasingly distinct boundaries. Internal to their boundary, snowflakes have some degree of structure, meaning that their component molecules and dynamics have a distinct morphology, and spatial and temporal organization. Because ice growth is sensitive to the temperature, humidity, pressure and other states in the local environment, the growth behaviour and morphology of snowflakes will change over time as they are passively dragged around. After some time, snowflakes will encounter a phase-boundary, at which the temperature in the environment will cause them to lose their boundaries and internal structure, and melt.
In fact, free-energy theorists want to account for both biological homeostasis and biological robustness at the same time, as they often emphasise that to the extent an organism minimizes its expected free energy, it will maintain its structural and functional organization amid change in the environment .
Homogeneous Equilibrium And Relaxation Models
In a homogeneous equilibrium model, all phases are assumed to be in dynamic and thermodynamic equilibrium. That is, they all move at the same velocity and have the same temperature. In addition, the pressure of the CO2 vapour is assumed to be equal to the saturation pressure whenever the condensed phase is present. The pressure of the condensed phase CO2 is also assumed to be equal to the combined pressure of CO2 vapour and air . These assumptions are reasonable provided any CO2 liquid drops or solid particles are sufficiently small. The computational implementation assumed that the mixture was in homogeneous equilibrium, i.e. that the solid/liquid and gas phases were well mixed and that the liquid drops or solid particles were sufficiently small. However, there are some indications from recent experimental work that this is not true. For the current model, a simple sub-model for the relaxation to equilibrium was therefore included. A full model would require the inclusion of drops or particles and is beyond the scope of the present work, but is under development.
D. Oken, in, 2001
You May Like: What Is Adhesion In Biology
Chemical Equilibrium And Le Chtelier’s Principle
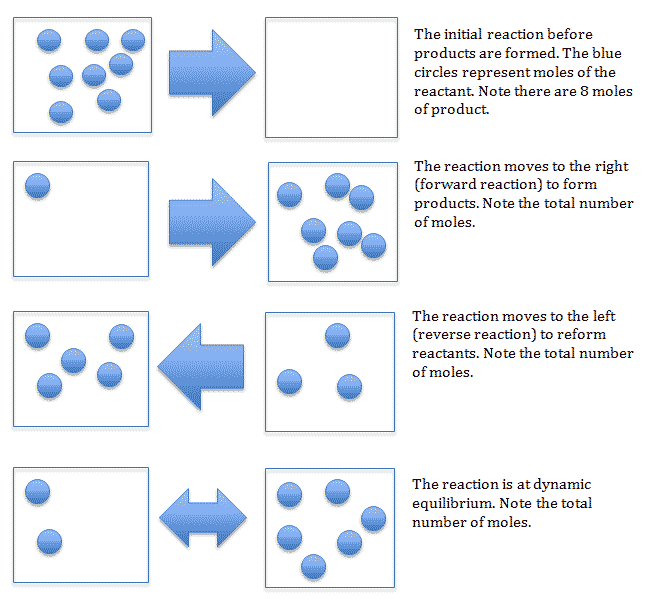
Le Châtelier was a French chemist most famous for his work on chemical equilibria. He proposed a principle to explain how systems in dynamic equilibrium respond to changing conditions.
Le Châtelier’s principle states if the conditions of a dynamic equilibrium in a closed system change, the position of the equilibrium will shift to counteract the change.
OK – how about that in plain English, please!
We know that if you take any reversible reaction and leave it in a sealed container for long enough, it will reach dynamic chemical equilibrium. The rates of the forward and backward reactions are the same, and the concentrations of products and reactants remain constant. However, Le Châtelier stated that if we change the conditions inside of the container, we can change the rates of the two reactions. For example, we could increase the temperature, and this may favour the forward reaction. Or we could increase the pressure, and this may favour the backward reaction. This is called shifting the position of the equilibrium. If we shift the equilibrium to the right, we say the equilibrium favours the forward reaction. If we shift it to the left, we say that it favours the backward reaction.
However, the change in rate isn’t random. The equilibrium system always tries to reduce the impact of the change in conditions.
Le Châtelier’s principle is useful because it allows us to influence the yield of a reversible reaction. Let’s look at some real-life examples.
Biological Systems As Random Dynamical Systems
In the previous sections, we pointed out that Friston and collaborators use the mathematics of random dynamical systems and statistical physics in order to build model-based representations of biological systems aiming to account for the conditions of possibility of biological persistence. We have also alluded to the active inference models grounded in the FEP .
Active inference models are phase-space representations of biological systems as forming expectations over observable external states and inferring policies that minimize the expected free energy of those states under a generative model in some pre-defined Markov decision process. By minimizing expected free energy, the modelled system would attain a non-equilibrium steady state, and so, it would maintain, in some sense, a low entropy probability distribution over its states.Footnote 5
An assumption made by the active inference models developed by free energy theorists is that target biological systems can be represented as random dynamical systems. What does this assumption mean exactly?
In other words, the ergodic density is an invariant probability measure that can be interpreted as the probability of finding the target system m in any state x when observed at a random point in time . The assumption of ergodicity is important to get the FEP off the ground, since it ensures that organisms can be modelled as having invariant characteristics over time.
Also Check: What Is The Rdw Process In Math
Is The Body Ever In Equilibrium
All the bodys systems work together to maintain a balanced internal environment, a process called Homeostasis. Homeostasis is a condition of optimal functioning for the organism and includes many variables such as body temperature and fluid balance. Have you ever felt tired for no apparent reason?
Reproductive Isolation Among Kingfishers
The study of kingfishers in Papua New Guinea showed the deep impact of reproductive isolation on speciation. There are three subspecies that reside on the mainland. Here, the environment can vary wildly from humid, dense rain forest to monsoon forests with extended dry seasons. These subspecies can not only interbreed but are nearly indistinguishable from each other.
However, on islands a few hundred kilometers away, even when the environment is similar to the nearest part of the mainland, the kingfishers are markedly different. More species have been found on these smaller islands than on the mainland. Similar observations have been made for birds and reptiles and invertebrates across the world, where geographical separation has led to the emergence of new species, while large continuous tracts with varying conditions maintain homogeneous populations. This evidence supports the punctuated equilibrium theory.
You May Like: Contributions To Algebra And Geometry Impact Factor