Infinitesimal Change Of Or D/dt
These infinitesimal changes are the fundamental concern of the differential calculus process of differentiation. Differentiation enables us to find instantaneous rates of change of literally any variable. That is what the addition of d/dt or the symbol d into an equation does. It turns it into a limit and tells us that we are differentiating to find instantaneous quantities.
Note that an infinitesimal change is not a quantity in and of itself. It tells us only that we are taking the limit of some function, finding the derivative at a given moment in time. In the case of something like velocity as we discussed above this looks like:
Where a is some instant in time we want to find the instantaneous velocity from. If we want to determine the velocity at t=3.0s into our measurements, then we will be seeking the limit as . These limits arise from the general calculus equation for calculating the slope of a graph over infinitesimal intervals of whatever the x- and y-axis units are.
In the case of velocity there is not a single value of displacement or time , but a range
If we are trying to find the instantaneous current within a conductor, then our general current expression where is the current in amps , is the amount of charge to pass a point of the conductor over a time interval in seconds. Then the symbol d/dt acts on the function, changing it, telling us to differentiate and find the limit as follows
Projectile Motion Solved Examples:
Example :
A projectile is fired at $150\,$ from a cliff with a height of $200\,$ at an angle of $37^\circ$ from horizontal. Find the following: the distance at which the projectile hit the ground. the maximum height above the ground reached by the projectile. the magnitude and direction of the projectile velocity vector at the instant of impact to the ground.
Solution:
Let the firing point be the origin of coordinate, $y$ is positive upward and $x$ is positive to the right. Since the projectile hit the ground below the considered origin so its coordinate is $$.
The formula for horizontal distance of a projectile is given by $\Delta x=\, t$, since we are asked to find the total distance from launching to striking point $$, which is the range of projectile, so the total time of flight is required which is obtained as below \ The solution to the quadratic equation $ax^2 + bx+c=0$ is given \ Using that, one can find the total time of flight as below \ Because the projectile fired at $t=0$ so the time of strike can not be a negative value. Thus, the total time is $t=20.757\,$. Now substitute it into the horizontal distance formula to find the RANGE of Projectile as below \
Example :
Solution:
The components of the velocity vector is determined as \ Thus, the vector addition of those components gets the velocity vector \
Solution:Known: $\theta=35^\circ$, Range of projectile $R=13.8\,$, Maximum height $H=2.42\,$.
Also Check: Does Mj Have Any Biological Kids
What Does Mean In Physics
In general physics, delta terms change and delta-v is simply a change in velocity. The Greek uppercase letter delta is the standard mathematical symbol to represent change in some quantity. That is a delta and it essentially means, a change in. x means a change in x. For example say you moved 2 feet forwards.
You May Like: How Do Nurses Use Chemistry
What Is The Meaning Of Following Expression $c=\frac$ Mathematically
Our professor raised the following question during our lecture in Statistical Physics :
Many text books writes wrong expressions for Heat Capacity Coefficient, and the right way to wright it is as following:$$C=\frac.$$But as we see it is neither usual differential, nor a functional derivative, so the question what is this?
I couldn’t find the answer in math books, and it is true that many text books writes it in very different ways mixing exact and inexact differentials, so anybody have a clue what is the right expression for c and why from mathematical point of view?
I) The use of $\delta$ in the derivative
$$C~=~\frac $$
is because in thermodynamics, heat $Q$ is not a state function. In particular, the differential $\delta Q$ is in-exact.
II) In detail, the heat capacity $C$ is not obtained by differentiation of some ordinary function wrt. temperature $T$. Rather it should be viewed as a ratio
$$C~=~\frac $$
where $\Delta T$ is sufficiently small .
- 1$\begingroup$Maybe your answer is the clearest one among others, but it doesn’t address the main issue, why we don’t use functional derivative? that Q is state function is known, why we not use $$\delta T$$ instead? and what is the meaning of dividing variation on infinitesimal differential , what is this Mathematically/Geometrically ?$\endgroup$
Let’s take a look at the meaning of $\delta Q=C\mathrm dT$ assuming differential forms:
A further note for the more mathematically inclined:
Life Death And What Does Delta T Mean In Physics

Much like anything, there architecture personal statement can be a good take away about student engagement, faculty, student solutions, and general reputation. With the expanding popularity of online universities the range of on-line degree programs keeps growing. In such a scenario, students may choose the course at another institution or decide to take it at the campus.
Also Check: Why Do People Stare Psychology
Icle Trajectories In Cylindrical
It is often convenient to formulate the trajectory of a particle r = , y, z) using polar coordinates in the XâY plane. In this case, its velocity and acceleration take a convenient form.
Recall that the trajectory of a particle P is defined by its coordinate vector r measured in a fixed reference frame F. As the particle moves, its coordinate vector r traces its trajectory, which is a curve in space, given by:
ijkXYZF
Consider a particle P that moves only on the surface of a circular cylinder r = constant, it is possible to align the Z axis of the fixed frame F with the axis of the cylinder. Then, the angle θ around this axis in the XâY plane can be used to define the trajectory as,
Rθθ
The cylindrical coordinates for r can be simplified by introducing the radial and tangential unit vectors,
Using this notation, r takes the form,
rRRθzvPr
Similarly, the acceleration aP, which is the time derivative of the velocity vP, is given by:
The term r }^\mathbf _} acts toward the center of curvature of the path at that point on the path, is commonly called the centripetal acceleration. The term 2 }}\mathbf _} is called the Coriolis acceleration.
You May Like: Biotic And Abiotic Meaning
Choosing Good What Does Delta T Mean In Physics
The simplest approach to understand that the idea entropy defines the direction of the stream of timemust be wrong, is to understand that theres no time Only now! If you would like to read more on the subject of Fourier Transforms, then the Better Explained article is a great start. Time dilation is amazing since it disagrees with our normal intuition.
Also Check: What Is Vo In Physics
The New Angle On What Does Delta T Mean In Physics Just Released
While DNA is the predominant foundation for life on Earth now, its been suggested that RNA might have dominated the initial lifeforms. This approach is called Fourier Analysis. So, now we truly have to confront the delta function.
At Franklin Pierce University, online students may pursue an on-line degree in a variety of academic places. We provide a Solution Library of already-prepared solutions for thousands and thousands of cases, assignments and textbook questions which are available for immediate download. You may also set up your very own interactive study planner to assist you work out your time ahead of significant exam dates.
Delta Symbol: Geometry And Angles
In the field of geometry, lower-case delta may be representative of an angle in any geometric shape. This is primarily because geometry has its roots in Euclids work of ancient Greece. Consequently, mathematicians marked their angles with Greek letters.
The knowledge and understanding of the Greek alphabet are not necessary. This is because the letters merely represent the angles.
Read Also: What Is Washing Soda In Chemistry
What Does D Or D/dt Mean
As you will know, in science the Greek letter capital delta refers to a change in a quantity or an interval of a quantity, such as an interval of time. It is used to signify that a variable is not static, and is dynamically changing from one moment to the next.
For example, if we are talking about velocity, specifically average velocity or speed, their equations can take the form of the following, respectively
in words as a change in The above equation have which is the change in displacement, and which is the change in position, both of which occur over the time interval . Therefore we verbalize the above equation by saying that the average velocity / speed is equal to the change in displacement / position divided by change in time.
This is what uppercase delta means, and is also what lowercase delta means as well. The only difference is that they refer to different magnitudes of change. Uppercase refers to a macro change. When dealing with velocity maybe a change in time that last from seconds, to minutes, or perhaps hours.
The lowercase delta refers to an infinitesimal change. When dealing with velocity then we are dealing with an infinitesimal change in displacement / position that takes place over an infinitesimal change in time. An infinitesimal change in time is not seconds but perhaps a millionth, billionth, or trillionth of a second. Corresponding respectively to a microsecond , nanosecond .
Difference Between $\delta$ $d$ And $\delta$
I have read the thread regarding ‘the difference between the operators $\delta$ and $d$’, but it does not answer my question.
I am confused about the notation for change in Physics. In Mathematics, $\delta$ and $\Delta$ essentially refer to the same thing, i.e., change. This means that $\Delta x = x_1 – x_2 = \delta x$. The difference between $\delta$ and $d$ is also clear and distinct in differential calculus. We know that $\frac$ is always an operator and not a fraction, whereas $\frac$ is an infinitesimal change.
In Physics, however, the distinction is not as clear. Can anyone offer a clearer picture?
- May 24, 2013 at 12:35
- 7$\begingroup$”We know that $\frac$ is always an operator and not a fraction, whereas $\frac$ is an infinitesimal change.” The operator would be $d/dx$, not $dy/dx$. Also, it is actually valid to consider $dy/dx$ as the quotient of two infinitesimal numbers. That’s how physicists, mathematicians, and engineers throught about it for hundreds of years after the invention of calculus, and Abraham Robinson proved ca. 1960 that it didn’t lead to logical inconsistency. There is even a freshman calc book using this approach: math.wisc.edu/~keisler/calc.html$\endgroup$ user4552May 24, 2013 at 12:52
- 1May 24, 2013 at 13:06
- 2May 24, 2013 at 13:43
- 2
The symbol $\Delta$ refers to a finite variation or change of a quantity by finite, I mean one that is not infinitely small.
Don’t Miss: What Is Copulation In Biology
A Proof Of The Existence And Uniqueness Of The Transformation
The feasibility of the transformation can be shown as a consequence of the superposition theorem for electric circuits. A short proof, rather than one derived as a corollary of the more general star-mesh transform, can be given as follows. The equivalence lies in the statement that for any external voltages ( V
c },R_},R_}} ), here it is straightforward to show that these equations indeed lead to the above designed expressions.
In fact, the superposition theorem establishes the relation between the values of the resistances, the uniqueness theorem guarantees the uniqueness of such solution.
Type Of What Does Delta T Mean In Physics
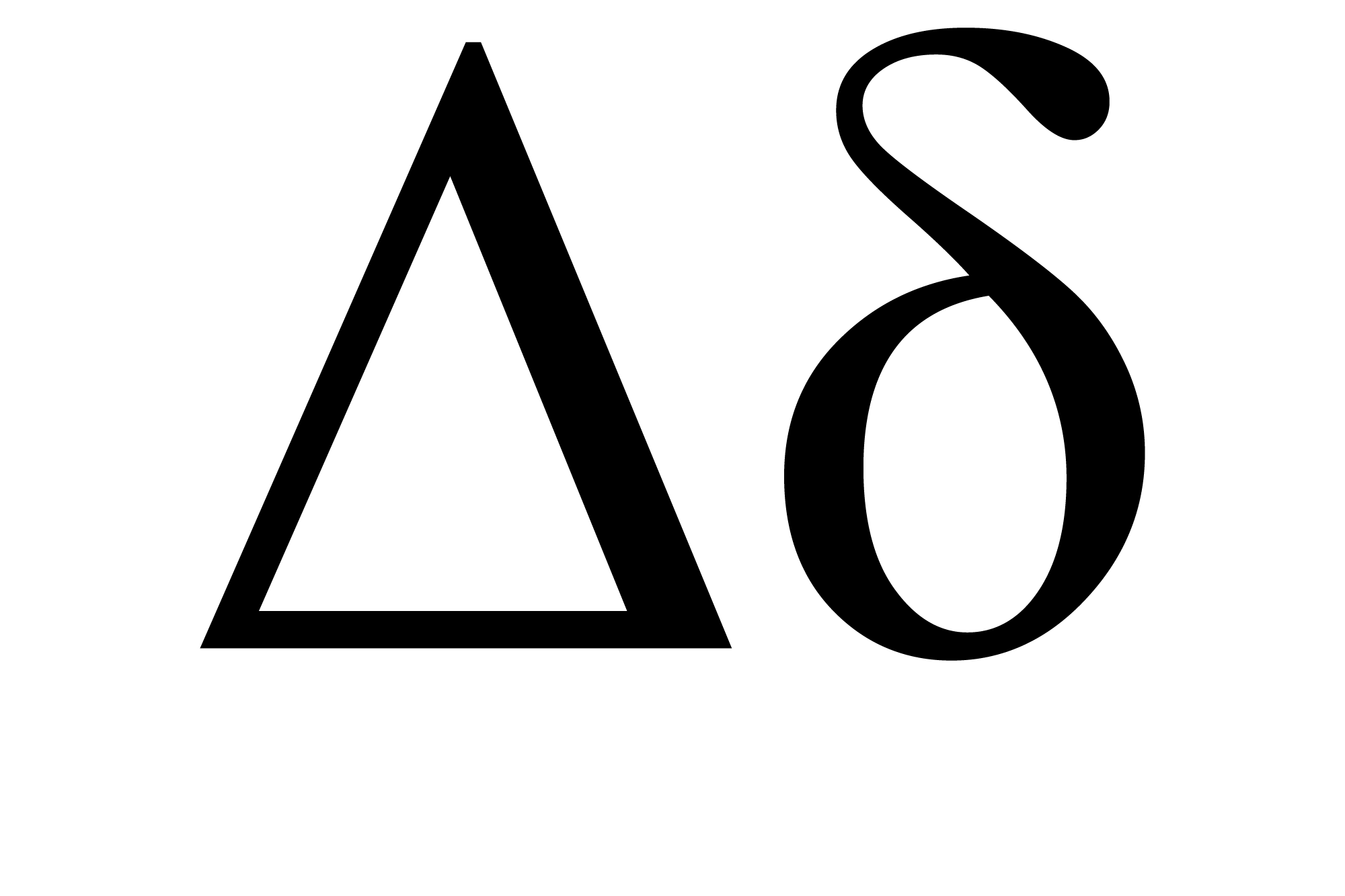
Theoretically, any substantial object can turn into a Black Hole. In truth, it could be that space must incorporate all possibilities as a way to seem empty to us. In this instance, the displacement is simply 3 meters to the right.
Our sheet is just supposed to highlight key equations which are most helpful for the their explanation new MCAT. The second principal benefit of quantum computing is that you could use qubits to send data in a means thats inherently secure. This value is represented by means of a percentage.
Also Check: How To Test For Pure Water Chemistry
What Can Be Done With A Deltav System
The inherent integration of the DeltaV system extends to batch, advanced control, change management, engineering tools, diagnostics, and more. The DeltaV systems embedded advanced control provides a full array of applications to improve control performance and optimize operations.
Which is the output of the delta modulator?
A Stair-case approximated waveform will be the output of the delta modulator with the step-size as delta . The output quality of the waveform is moderate. The delta demodulator comprises of a low pass filter, a summer, and a delay circuit. The predictor circuit is eliminated here and hence no assumed input is given to the demodulator.
Introduction To Delta Symbol
The fourth letter of the Greek alphabet refers to the delta. Delta symbol was derived from the Phoenician letter dalet . Furthermore, the delta is a symbol that has significant usage in mathematics.
Delta symbol can represent a number, function, set, and equation in maths. Student can learn more about the delta symbol and its meaning in maths here.
Read Also: Holt Geometry Lesson 4.5 Practice B Answers
Solved Question For You
Q1. Which of the following statements is not true with regards to the delta symbol in maths?
A. In trigonometry, lower-case delta represents the area of a triangleB. Uppercase delta at oftentimes means change or the change in maths.C. Uppercase delta in algebra represents the discriminant of a polynomial equation.D. In geometry, lower-case delta may be representative of an angle in any geometric shape
A1. The correct answer is option A., Which is In trigonometry, lower-case delta represents the area of a triangle. This is because lower-case delta does not represent the area of a triangle in trigonometry.
Download Toppr app for Android and iOS or signup for free.
What Is The Formula Of U V
The Product and Quotient Rules are covered in this section. This is used when differentiating a product of two functions. d = + x = x² + 1 + 2x² = 3x² + 1 .
How do you differentiate equations?
In implicit differentiation, we differentiate each side of an equation with two variables by treating one of the variables as a function of the other. This calls for using the chain rule. Lets differentiate x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1x, squared, plus, y, squared, equals, 1 for example.
What is H in derivatives?
The value of. ffh. is the slope of the line through the points ) and ), the so called secant line. Note that x=a+ha=h and y=ff. The limit of the secant lines as h tends to zero is the tangent line.
Why is it called derivative?
I believe the term derivative arises from the fact that it is another, different function f which is implied by the first function f. Thus we have derived one from the other. The terms differential, etc. have more reference to the actual mathematics going on when we derive one from the other.
How do you differentiate students?
Differentiated instruction in the classroom can be done several ways. Grouping, varying amounts of time, or changing the task are the most common types of differentiation. As far as grouping goes, students can be grouped by ability level, interests, or intermingled levels of understanding.
What are the five instructional strategies?
Consider the five categories of instructional strategies .
Don’t Miss: How To Do Ratios In Math
What Does Delta Mean In An Equation
Delta Symbol: Change Uppercase delta at most times means change or the change in maths. Consider an example, in which a variable x stands for the movement of an object. So, x means the change in movement. Scientists make use of this mathematical meaning of delta in various branches of science.
What does lowercase delta mean in chemistry?
Delta , is a letter of the Greek alphabet, used to represent the d sound in Ancient and Modern Greek. In molecular chemistry, the lower case Greek letter is used to represent a partial charge.
What does mean in physics?
What does mean in physics? In general physics, delta terms change and delta-v is simply a change in velocity. The Greek uppercase letter delta is the standard mathematical symbol to represent change in some quantity. Depending on the situation, delta-v can be either a spatial vector or scalar .
Three Dimensional Delta Function
The delta function can be promoted to a three-dimensional version. We simply merge three of them together, one for each dimension. The definition is
\begin \delta := \delta \delta \delta, \tag \end
where $$ are the variables contained in $\boldsymbol$, while $$ are those contained in $\boldsymbol$. The three-dimensional delta function refers to two positions in space, and it can be considered a function of either $\boldsymbol$ or $\boldsymbol$ it is an example of a two-point function. Its action on a test function $f$ is given by
\begin \int f \delta\, dV = f, \tag \end
where the integration is over three-dimensional space, and $dV := dxdydz$ is the volume element.
Equation is a natural generalization of Eq., but it is in fact a direct consequence. To see this, let us write $f$ explicitly as $f$, and insert the definition of Eq.. We get
\begin \int f \delta\, dV = \int_^\infty \int_^\infty \int_^\infty f \delta \delta \delta\, dxdydz, \tag \end
and we can do each integral one by one. Performing the $x$-integral gives
\begin \int f \delta\, dV = \int_^\infty \int_^\infty f \delta \delta\, dydz, \tag \end
with the function now evaluated at $x=x$. Performing the $y$-integral gives
\begin \int f \delta\, dV = \int_^\infty f \delta\, dz, \tag \end
and the last step returns
\begin \int f \delta\, dV = f = f, \tag \end
as expected.
\begin \int f \delta\, dV = f, \tag \end
\begin \int \int \int f \delta\, h_1 h_2 h_3\, dq_1 dq_2 dq_3 = f, \tag \end
- 2
- 0
You May Like: How To Break Habits Psychology