Check If The Given Two Numbers Are Friendly Pair Or Not
Given two positive integer N, M. The task is to check if N and M are friendly pair or not.
In number theory, friendly pairs are two numbers with a common abundancy index, the ratio between the sum of divisors of a number and the number itself i.e ?/n. S o, two number n and m are friendly number if ?/n = ?/m. where ? is the sum of divisors of n.
Examples:
Input : n = 6, m = 28Output : YesExplanation:Divisor of 6 are 1, 2, 3, 6.Divisor of 28 are 1, 2, 4, 7, 14, 28.Sum of divisor of 6 and 28 are 12 and 56respectively. Abundancy index of 6 and 28 are 2. So they are friendly pair.Input : n = 18, m = 26Output : No
The idea is to find the sum of divisor of n and m. And to check if the abundancy index of n and m, we will find the Greatest Common Divisors of n and m with their sum of divisors. And check if the reduced form of abundancy index of n and m are equal by checking if their numerator and denominator are equal or not. To find the reduced form, we will divide numerator and denominator by GCD.Below is the implementation of above idea :
Thbit Ibn Qurra Theorem
The Thbit ibn Qurra theorem is a method for discovering amicable numbers invented in the ninth century by the ArabmathematicianThbit ibn Qurra.
It states that if
- p = 3×2n 1 1,
- q = 3×2n 1,
- r = 9×22n 1 1,
where n> 1 is an integer and p, q, and r are prime numbers, then 2n×p×q and 2n×r are a pair of amicable numbers. This formula gives the pairs for n = 2, for n = 4, and for n = 7, but no other such pairs are known. Numbers of the form 3×2n 1 are known as Thabit numbers. In order for Ibn Qurra’s formula to produce an amicable pair, two consecutive Thabit numbers must be prime this severely restricts the possible values of n.
To establish the theorem, Thâbit ibn Qurra proved nine lemmas divided into two groups. The first three lemmas deal with the determination of the aliquot parts of a natural integer. The second group of lemmas deals more specifically with the formation of perfect, abundant and deficient numbers.
Euler’s rule is a generalization of the Thâbit ibn Qurra theorem. It states that if
- p = ×2m 1,
- q = ×2n 1,
- r = 2×2m + n 1,
where n> m> 0 are integers and p, q, and r are prime numbers, then 2n×p×q and 2n×r are a pair of amicable numbers. Thbit ibn Qurra’s theorem corresponds to the case m = n 1. Euler’s rule creates additional amicable pairs for = , with no others being known. Euler overall found 58 new pairs increasing the number of pairs that were then known to 61.
Using Friendly Numbers: An Addition Strategy
WHAT IS A FRIENDLY NUMBER?
In this case, we refer to friendly numbers as a number that is easy to work with. For example, multiples of 10 are friendly because they are easy to work with when we add or subtract.
USING FRIENDLY NUMBERS AS AN ADDITION STRATEGY
When we use the friendly number strategy for addition, it helps us work with big numbers. This is because we are essentially breaking the equation up into more manageable parts.
We begin by getting to a friendly number, which is typically a multiple of 10, 100, or 100 depending on the numbers that we are working with. Then we add on the remainder.
Lets take a look at the using friendly numbers addition strategy in action.
EXAMPLES
In this example we will add 27+9 using the friendly number strategy.
First, lets put the number 27 on our empty number line.
Now lets get to a friendly number. We know that the number 30 is friendly or easy to work with, so we can add 3 to get to 30.
Lastly, we add the remaining 6 and get our answer of 36.
Suppose we are solving 265+18.
First we will write 265 on our empty number line.
Then we can add 5 from the 18 to get to a friendly number 270.
We have 13 left, so now we can simply add the 13 to the 270 to get a final answer of 283.
BIG IDEAS
Mental Math is not about following a one size fits all process or procedure. Mental Math involves being able to think flexibly about numbers and manipulate them in different ways.
Read Also: Do I Capitalize Bachelor’s Degree In Psychology
References In Popular Culture
- n k )=\sigma =\dots =\sigma =n_+n_+\dots +n_}
For example, is an amicable triple , and is an amicable quadruple .
Amicable multisets are defined analogously and generalizes this a bit further .
Sociable numbers are the numbers in cyclic lists of numbers where each number is the sum of the proper divisors of the preceding number. For example, 1264460
Number Lines And Friendly Numbers
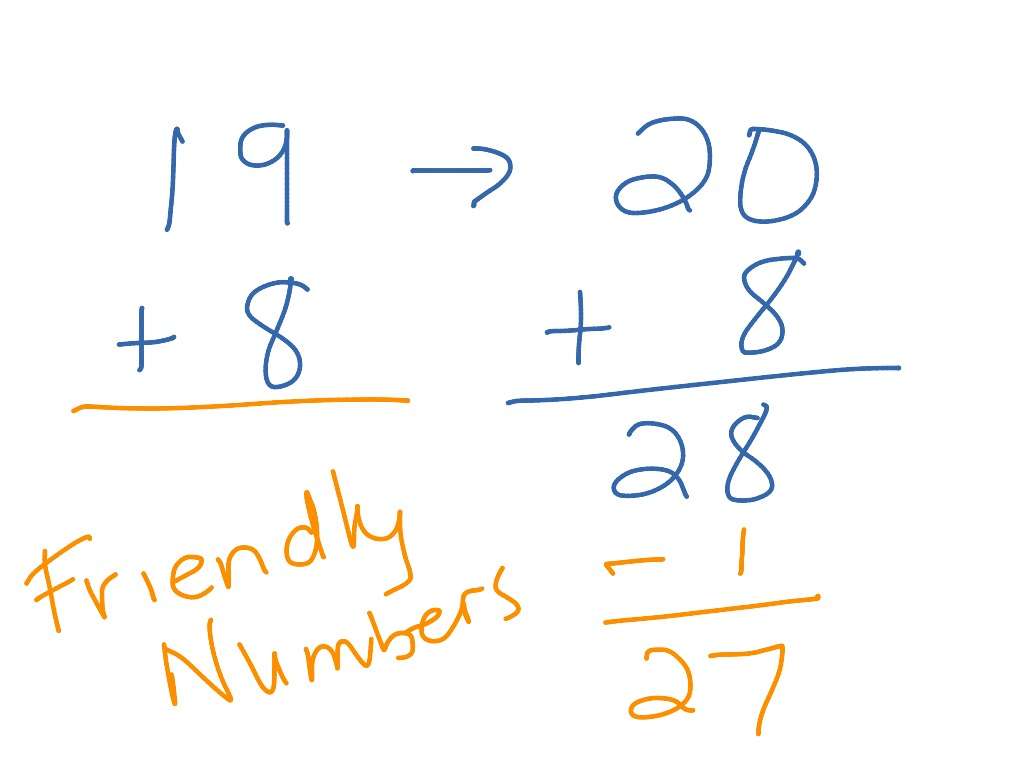
Do you use number lines in your math class? Number lines are a great tool for students to use, especially for addition and subtraction. Most of us are familiar with the standard number line that is already labeled for us:
However, an empty number line can be a more useful tool for students to use, and can be drawn quickly and easily on the side of an activity page or a scrap piece of paper. All the student needs to do is draw a straight line!
When using an empty number line, I like to talk to the students about friendly numbers. A friendly number is simply a number that is easy to work with. This normally refers to multiples of 10. Heres an example of using an empty number line for the equation 18+5.
First, draw a line and label the 18. Then, it is time to find a friendly number. The number 20 is friendly, so we draw a line and label it 20, and then add the +2 above the line to show that we have added a total of 2. Now, to add a total of 5, we need to add 3 more. We can now easily add 3 to the 20 to make a total of 23. Make sense?
Heres another example, this time a bit harder. Lets try the equation 27+19.
Empty number lines can also easily be used with subtraction. With subtraction, you can start with the largest number and count back, using friendly numbers along the way.
See you again soon,
You May Like: Simplifying Radicals Worksheet 2
Guide For The Instructor
Most of the non-numerical exercises in this book are designed tofoster discussion and experimentation. They do not necessarily have”correct” or “complete” answers. Many students will find thisextremely disconcerting at first, so it must be repeatedly stressed.You can make them feel more at ease by prefacing such questions withthe phrase “Tell me as much as you can about…” Tell yourstudents that accumulating data and solving special cases are notmerely acceptable, but encouraged. On the other hand, tell themthat there is no such thing as a complete solution, since the solutionof a good problem will always raise additional questions. So if theycan fully answer the specific question given in the text, their nexttask is to look for generalizations and for limitations on thevalidity of their solution.
Number theory is not easy, so there’s no point in trying to convincethe students that it is. Instead, this book shows the readerthat he or she is capable of mastering a difficult subject andexperiencing the intense satisfaction of intellectual discovery.The instructor’s reward is to bask in the glow of their endeavors.
Maths For Valentines Day What Are Friendly Numbers
Home/Maths for Valentines Day What are Friendly Numbers?
How many roses or chocolates should you buy your loved one on Valentines Day? To a lot of people, numbers are hugely symbolic and buying your Valentine 13 Roses could easily send the wrong message. If your Valentine loves maths, then a Friendly Number could be your thing the numerical equivalent of a stuffed bear holding a sparkly heart.
A note of caution the opposite of a Friendly Number is known as a Solitary Number and these are probably best avoided with your Valentine. Even worse than this, there is an Undecided Category which contains numbers where nobody can currently prove whether they are Friendly or Solitary you may as well just set your relationship status on Facebook to Its Complicated.
Recommended Reading: Are Elton John’s Kids His
Friendly Numbers Under 100
If you want a Friendly number which is relatively small and therefore actually useful on Valentines day then take your pick from Friendly Numbers which are under 100. But you must be careful, because most of these numbers are not friendly with each other. For example, the abundancy of 6 is equal to 2, whereas the abundancy of 12 is equal to . The number 6 is a friendly number because it has friends but it is certainly not friends with every other Friendly Number!
Friendly numbers under 100: 6, 12, 24, 28, 30, 40, 42, 56, 60, 66, 78, 80, 84, 96
Computers Number Theory And This Book
However, just as with any good rule, certain exceptions will beadmitted. First, one of the best ways to understand a subject is toexplain it to someone else so if you know a little bit of how towrite computer programs, you will find itextremely enlightening to explain to a computer how to perform thealgorithms described in this book. In other words, don’t rely on acanned computer package, do the programming yourself. Good candidatesfor such treatment are the Euclidean algorithm ,RSA encoding and decoding , quadraticreciprocity , writing numbers as sums of two squares, and adding rational points on elliptic curves. The second exception to the “no computer rule” isgeneration of data. Discovery in number theory is usually based onexperimentation, which may involve examining reams of data to tryto distinguish underlying patterns. Computers are well-suited togenerating such data, and also sometimes to assist in searchingfor patterns, and I have no objection to their being used for thesepurposes. The moral is that computers are useful as a tool forexperimentation, and that one can learn by teaching a computer how toperform number theoretic calculations, but prepackaged programsmerely provide a crutch which will prevent you from learning to walkon your own.
You May Like: Beth And John Thomas Child Of Rage Now
Definition Of A Friendly Number
If a number has the same abundancy as another number, then it is a Friendly Number!
Number 6 is a friendly number because it has another friend in the form of the Number 28, they both have an Abundancy equal to 2.
This means that 6 and 28 are friendly with each other. The numbers 6 and 28 are also really special because they are Perfect Numbers they are the sum of their proper factors e.g. 1+2+3=6 and 1+2+4+7+14=28. This means that 6 and 28 are friendly with all other Perfect Numbers, because every Perfect Number will have an abundancy equal to 2. Mathematicians have yet to prove whether the group of Perfect Numbers is infinitely big. Does 6 have an infinite number of friends we dont yet know!