How Do You Translate A Word Problem Into An Equation
How to Convert Word Problems Into Equations
A Tricky Math Problem Created By Gergely Duds Used Ice Cream Cones Instead Of Variables
Artist Gergely Dudás, who is known for his tricky hidden-object puzzles, shared a math problem on his that he illustrated with ice cream cones.
The brainteaser consists of four math equations, each of which adds to or multiplies a numerical sum or product. In place of variables like x or y, however, the brainteaser substitutes ice cream cones that are either empty or have scoops of white ice cream, pink ice cream, or both.
To solve the puzzle, you have to figure out what number the empty ice cream cones, white ice cream scoops, and pink ice cream scoops each represent.
The answer is that the empty ice cream cone represents the number three, the white ice cream scoop represents the number two, and the pink ice cream scoop represents the number one.
The Hardest Math Problem Is This:
Still feeling confident right there? People online are coming up with a barrage of different answers. Its gotten to a point where they cant decide what the correct answer is, but its actually a simple PEMDAS operation and the final answer is set in stone.However, the more contradicting the answers are, the more viral a question will go. Have you solved it yet? If your answer is zero, four, seven, or a decimal fraction, you might want to take another go at it before taking a peek at the solution. Think of this as a brain teaser, and while they may be a bit pesky sometimes, they are certainly interesting and great for improving your memory and processing abilities. While youre at it, lets talk a bit about how the Order of Operation which is known as PEMDAS came to be. Its not all Euclid and Pythagoras. Our helpful Parentheses/Brackets Exponent Multiplication Division Addition and Subtraction had to have come from somewhere right?While the actual origin and inventors have remained unknown for decades, historians say that the Order of Operation was created out of a desperate need for simplified solutions. As early as the 6th Century BC, people needed math to keep count of their animals, crops, and carry out trades. Many communities invented their own systems of counting. For instance, the Babylonians worked with a system based on 60, while most others took their measurements in 10s.
Don’t Miss: Kuta Software Volume Of Prisms And Cylinders
A Math Problem Meant For 8
Mumsnet user lucysmam turned to the internet for help with her daughter’s math assignment.
The problem reads as follows:
“On the coast there are three lighthouses.
The first light shines for 3 seconds, then is off for 3 seconds.
The second light shines for 4 seconds, then is off for 4 seconds.
The third light shines for 5 seconds, then is off for 5 seconds.
All three lights have just come on together.
1) When is the first time all three lights will be off at the same time?
2) When is the next time all three lights will come on together at the same moment?”
Thankfully, YouTube math whiz Presh Talwalkar offered an explanation on his channel, MindYourDecisions.
According to Talwalkar, the easiest way to answer the first question about when the lights will all be off is to map out the intervals for each lighthouse and see where their “off” sections overlap. The answer: after five seconds, when the third light has just turned off and the first and second lights are still off.
To determine when all of the lights will come on together, you need to find the smallest common multiple of the intervals when the lights will be on. The answer to that question is that the lighthouses will all come on together at 120 seconds, or two minutes.
For a more detailed explanation, .
Students Produce 15 To 20 Pages Per Problem Set

Most Math 55 students produce 15- to 20-page problem sets each week. They have to produce so much, that students are sometimes discouraged from showing too much of their work.
As one former 55er explains, “Lots of students write out the solutions in lemma-theorem form, proving everything from rock bottom. I did this also. This makes your problem set enormous. You should learn what the main idea of the proof is, and what can be taken for granted. This is not so easy to do in an undergraduate proof class, where nearly all the proofs are of obvious facts.”
You May Like: Half-life Formula Chemistry
Professors Try To Get Students To Drop The Class
Professor Yum-Tong Siu, whose class began with 50 students in 2003, said he actively tried to whittle down the class size. As The Harvard Independent reports, the class dropped down to 25 students, but Siu added: “I want to reduce it a bit more.” The goal: 20. “We want a group of students with similar backgrounds so we can proceed at a pace that can suit them at the same time, so they don’t feel bored or over their heads,” said Siu.
You Can’t Double Major If You’re Taking Math 55
Those who plan on enrolling in Math 55 are warned that math must be their thing. This is not a class for dilettantes looking to major in philosophy or squeeze in some political science on the side. As the freshman guide warns, Math 55 is only for those who “are fairly certain that you want to be a math concentrator” and who “want math to be your most important class.”
Don’t Miss: Who Are Paris Jackson’s Biological Parents
Math 55 Is Like A Full
According to a freshman guide to Harvard’s Mathematics Department, there are two first-year math courses, the hardest one being Math 55. You could take Math 21, which is taught by graduate students and where homework usually takes a reasonable three to six hours per week. Or, you could opt to take Math 55which gives you 10 times the amount of homework.
“Problem sets can take anywhere from 24 to 60 hours per week to complete.” Yes, per week. So, basically, it’s a full-time job, plus a part-time joband that’s on top of the rest of your course load, internships, any actual part-time gigs, and requisite Harvard partying.
Time To Test Your Brain
These hard math problems arent straightforward arithmetic. Theyll challenge you to look at the problems a different way and test your logic and problem-solving skills while youre solving. And if math isnt your strong suit, take heartmost of these hard math problems just use very simple numbers with only basic operationsaddition, subtraction, multiplication, and division. What makes them a challenge is often examining the problem to find out the trick, or the pattern and the way the numbers relate to one another. Others require a fill-in-the-blank technique that requires you to use trial and error and work backward. Time to put your brainpower to work!
Also Check: What Happened To Beth Thomas Brother Jonathan
This Is The Hardest Math Problem In The World
What is the hardest math problem in the world? The answer to that question is tricky. Difficulty is a subjective metric and what is difficult for some may not be difficult for others. Some math problems, such as the infamousquestion 6 of the 1988 Math Olympiad are easy to understand but monstrously complex to solve. Others such as the7 Bridges of Königsberg problem seem complex but have a deceptively simple answer.
A reasonable metric to determine how difficult a math problem is could be the number of people that have solved it. Therefore, it stands to reason that the hardest math problems in the world are ones that no mathematician has solved yet. With that in mind, we are going to take a look at 6 of the most difficult unsolved math problems in the world.
Brief Overview Of The Act Math Section
Like all topic sections on the ACT, the ACT math section is one complete section that you will take all at once. It will always be the second section on the test and you will have 60 minutes to completed 60 questions.
The ACT arranges its questions in order of ascending difficulty. As a general rule of thumb, questions 1-20 will be considered easy, questions 21-40 will be considered medium-difficulty, and questions 41-60 will be considered difficult.
The way the ACT classifies easy and difficult is by how long it takes the average student to solve a problem as well as the percentage of students who answer the question correctly. The faster and more accurately the average student solves a problem, the easier it is. The longer it takes to solve a problem and the fewer people who answer it correctly, the more difficult the problem.
All that being said, with very few exceptions, the most difficult ACT math problems will be clustered in the far end of the test. Besides just their placement on the test, these questions share a few other commonalities. We’ll take a look at example questions and how to solve them and at what these types of questions have in common, in just a moment.
Don’t Miss: Afda Mean Median Mode Range Practice
Im Not Interested In Money Or Fame
Much has been made of the fact that a woman has been awarded one of this years four awards for the first time in the history of the prize. Maryam Mirzakhani works in the field of geometry and the description about her work reads: Because of its complexities and inhomogeneity, moduli space has often seemed impossible to work on directly. But not to Mirzakhani. She has a strong geometric intuition.
But the British community of mathematicians has also been delighted about Martin Hairers award only the eighth Briton to win the prize ever. He works in the field known as stochastic analysis. So far, so impossible to understand. But Professor Lyon saidhis the area builds on a field that has had a huge impact on everything from mobile phones to the stock market.
And experts have even speculated that his work could shed some light on another of those so-far unsolvable problems the Navier Stokes problem, which is one of six remaining unsolved Millennium Prize Problems, which include the Riemann hypothesis.
But then again, not all mathematicians are in it for the glory. The Russian genius Grigori Perelman famously rejected the Fields Medal and an additional $1m in 2010 for proving the Poincare conjecture, then one of the worlds most difficult problems.
Question 1: Calculator Permitted Multiple Choice
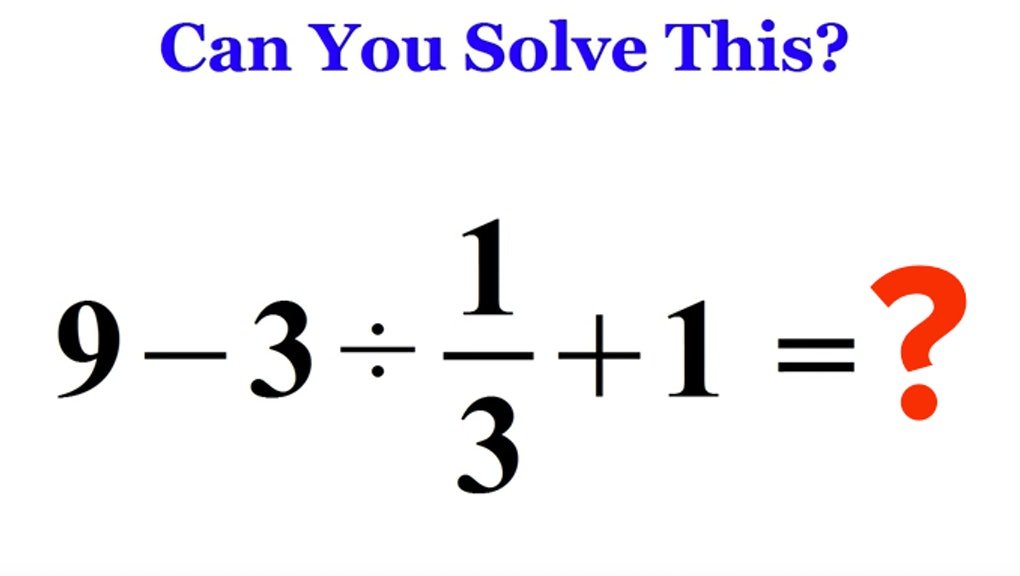
Answer: C
Category: Heart of Algebralinear equations and inequalities in context
Heres how you solve it:
1. Youll need to be able to write equations that reflect the context described in a word problem for several questions on the SAT, both linear context and non-linear contexts. If you have trouble translating word problems into math, this is a skill youll want to work on! Rewriting word problems to include words like equal to, less than, more than, sum, and so on can help you easily translate the problem into equations and inequalities.
2. Were told that Roberto wanted to sell \ insurance policies but he didnt meet his goal, which means that he sold less than \ insurance policies. Given that \ represents the number of \ policies sold and \ represents the number of \ policies sold, the sum of these two numbers is less than \. This is represented as \. We can eliminate choices B and D.
3. Next, were told that the value of all the policies sold was more than \. We need to multiply the value of the policy by the number of that type of policy, which gives us \. Choice C is the only answer that reflects Robertos insurance policy sales.
You May Like: Calculate Displacement Physics
Former International Math Olympiad Competitors Are Often Your Classmates
According to the freshman guide, Math 55 “often contains former members of the International Math Olympiad teams.” That’s the worldwide championship competition in which high school math students from more than 100 countries go head-to-head on ridiculously tough math problems.
For example, here’s a problem from last year’s battle:
A convex quadrilateral ABCD satisfies AB · CD = BC · DA. Point X lies inside
ABCD so that
XAB = XCD and XBC = XDA.
Prove that BXA + DXC = 180
Good luck.
Question : Calculator Not
Answer: B
Category: Passport to Advanced Mathrational equations
Heres how to solve it:
Recommended Reading: Abiotic Science Definition
What Is The Hardest Math Problem In The World
What is the hardest math problem in the world?
What is the hardest math equation in the world? In 2019, mathematicians finally solved a math puzzle that had stumped them for decades. Its called a Diophantine Equation, and its sometimes known as the summing of three cubes: Find x, y, and z such that x³+y³+z³=k, for each k from 1 to 100.
What math equation is impossible? For decades, a math puzzle has stumped the smartest mathematicians in the world. x3+y3+z3=k, with k being all the numbers from one to 100, is a Diophantine equation thats sometimes known as summing of three cubes.
What is Z+ in math? Z+ is the set of all positive integers , while Z- is the set of all negative integers . Zero is not included in either of these sets . Znonneg is the set of all positive integers including 0, while Znonpos is the set of all negative integers including 0.
Question : Calculator Permitted Grid
Answer: 750
Category: Heart of Algebrasystems of linear inequalities
Heres how to solve it:
Don’t Miss: Linear Algebra What Is Span
The Hardest Math Problem
Not about coronavirus just to cheer you up:
Puzzle. What math problem has taken the longest to be solved? It could be one thats solved now, or one thats still unsolved.
Lets start by looking at one candidate question. Can you square the circle with compass and straightedge? After this question became popular among mathematicians, it took at least 2296 years to answer it!
Its often hard to find when a classic math problem was first posed. As for squaring the circle, MacTutor traces it back to before Aristophanes wacky comedy The Birds:
So, quite conservatively we can say that the squaring the circle was an open problem known to mathematicians since 414 BC. It was proved impossible by Lindemann in 1882, when he showed that e
The Gauntlet Is Thrown
At the start of the millenium, the Clay Mathematics Institute put forward these seven problems which are deemed as some of the most difficult problems that remain open. Each problem has a one million dollar bounty for the first person to provide a valid proof .
I have been wanting to write this article for quite some time, but struggled to decide at what level I should present the material. After a lot of umming and ahing I decided to present it at an elementary university level. A few things will be assumed but everything that I think is new will be explained.
At the time I am writting this, only the Poincaré conjecture has been solved. Grigori Perelman presented the proof in 2003 and he was officially awarded the Millenium Prize in 2010 which he declined.
I will be presenting this conjecture first and then the remaining unsolved problems in order of increasing complexity.
You May Like: Unit 1 Geometry Basics Homework 2 Segment Addition Postulate Answers