What Are Collinear Points In Geometry

How To Determine If Points Are Collinear In Coordinate Geometry

How to prove if points are Collinear in coordinate geometry?

Collinear points definition:

• Three or more points that lie on a same straight line are called collinear points.
• Consider a straight line L in the above Cartesian coordinate plane formed by x axis and y axis.
• This straight line L is passing through three points A, B and C whose coordinates are , and respectively.
• Three or more points which lie on a same straight line are called collinear points.

How to find if three points are collinear?:

• There are two methods to find if three points are collinear.
• One is slope formula method and the other is area of triangle method.
• Slope formula method to find that points are collinear.
• Three or more points are collinear, if slope of any two pairs of points is same.
• With three points A, B and C, three pairs of points can be formed, they are: AB, BC and AC.
• If Slope of AB = slope of BC = slope of AC, then A, B and C are collinear points.

Example

Show that the three points A , B and C are collinear.

Solution:

It is

In the formula above, the two vertical bars enclosing the variables represent a determinant.

Let us apply the coordinates of the above three points A, B and C in the determinant formula above for area of a triangle to check if the answer is zero.

Since the result for area of triangle is zero, therefore A , B and C are collinear points.

Introduction To Collinear Points

Collinear points are the set of three or more points that exist on the same straight line. Collinear points may exist on different planes but not on different lines. The property of points being collinear is known as collinearity. So any three points or more will only be collinear if they are in the same straight line. Only one line is possible that can go through three different points which are collinear. In the image given below, points P, Q, and R are the collinear points.

How Do You Know If Points Are Collinear

To know whether the points are collinear or not we use various formulas. The basic and most commonly used formulas are

• Distance Formula
• Slope Formula
• Area of Triangle Formula

with the help of these formulas, we find out whether the points are collinear or not.

• In the distance formula, we find the distance between the first and the second point, and then the distance between the second and the third point, and then check if the sum of these two distances is equal to the distance between the first and the third point. This will only be possible if the three points are collinear points.
• We apply the slope formula, to find the slope of lines formed by the 3 points under consideration. If the 3 slopes are equal, then the three points are collinear.
• And in the area of the triangle formula, we use the fact that a triangle formed by three collinear points will have no area since it will just be a line joining the three points. So if we have three collinear points, we assume that they form a triangle, and calculate the area of the triangle, and if we get the result as 0, then the points must be collinear points.

You May Like: Eoc Fsa Warm Ups Algebra 1 Answers

What Are Collinear Points In Triangle

According to Euler’s theory, in a triangle, there exists an Euler line, in which three points of concurrency of the triangle lies. The three points which lie on the Euler’s line are the orthocenter, the circumcenter, the centroid. Hence the given points of concurrencies of the triangle are the collinear points in a triangle.

Understanding The Concept Better

Line Segment: A part of a line that is bounded by two endpoints. It is the shortest distance between two points and has a fixed length.

RAY: A ray in geometry can be defined as a line with a fixed starting point and no endpoint. It can infinitely extend towards a single direction or may pass through multiple points.

Point: A point indicates a position or location in space. A point has no shape or size and is represented by a small dot. Example: . A or Point A.

Plane: Plane is a flat two-dimensional surface which may contain points, lines, segment, etc

You May Like: Algebra 1 Age Word Problems

Formulas Used For Collinear Points

You can find Collinear points using two methods:

• Slope Formula
• Area of Triangle

Slope Formula: The Slope formula is measured as the ratio of the change in the Y-axis to the change in the X-axis. The straight-line slope will describe the steepness of the lines angle from the horizontal, whether it is rising or falling. If its neither rising nor falling, then the value of the slope will be zero.

The formula to calculate slope is,

m= y2-y1/x2-x1

Where m= slope of the line

Let us solve a sample question.

Question: Prove that the three points R S & T are collinear

Ans: If R S and T are collinear, then the slopes of any of the two pairs will be equal.

Using Slope formula:

Slope of RS= / = 1Slope of ST =/ = 1Slope of RT =/ = 1

Since slopes of any two pairs out of the given 3 pairs are equal, then it proves R, S, and T are Collinear.

Area of a triangle: If an area of a triangle is formed by three points is zero, they are collinear. When three sets of points are collinear, then they cannot form a triangle.

Area of Triangle is measured by,

½ Y1-y2 y2-y3

Lets solve an equation using the above-given coordinates using the area of triangle formula to check if the answer is Zero.

½ = ½ = ½ =0 4-6 6-8. -2 -2

Here, the result of the formula area of the triangle is zero. So R, S, and T are collinear points.

Example of Non-collinear points

Question: What is the least number for a Non-collinear point required to determine a plane is

1. 13. 34. Infinite

What Are Collinear Points In Geometry

Geometry is considered to be one of the most important subjects in school. While it may seem confusing at first, there are a few simple things that you can do in order to better understand and remember these concepts. In this article, let us understand and learn about collinear points.

Collinear points have three or more points aligned on a straight line. If we take some real-life example of collinearity, it would be like people standing in a queue. Hence, we can say collinear points are all situated on the very same line itself. In cartesian geometry, it is said that if the area formed by the given points is zero, then the points can be said to be collinear. For more facts on collinear points, .

Collinear points are important for geometry because it helps us identify the angles of any two lines when there are multiple points between them. It allows us to see if two lines intersect at all, what is the exact point of intersection which is called the point of concurrency. Collinear points can be said to be aligned, or they can be said to be in a row.

Geometry starts with the basics of points, moving on to lines and then the shapes formed by these points and lines, or their intersection. In Euclidean geometry, Euclid defined a line as breadthless length and a straight line as a line that lies equally with the points on itself when he first formalized geometry.

Also Check: Algebra 1 Age Word Problems

Collinear Points In Real Life

Anytime you have a series of individual items in a single straight line, you have models of collinear points. Suppose you have eggs in a carton each egg in one row is a collinear point:

Students seated at a long cafeteria table are collinear. Football players on the line of scrimmage are collinear. Rings on a shower curtain, plants in one row in a garden, numbers on a ruler, moviegoers in a ticket line, and commuters seated on a train are collinear.

For real-life examples to be good models of collinear points, you need to be able to draw a straight line through them. Think of the individual kernels on one row of an ear of corn.

Collinear foods are found all over the globe. In Japan, people enjoy Dango sweet little dumplings arranged three to five on a skewer.

Sosatie is a South African dish of little cubes of lamb or mutton interspersed with dried apricots, red onions, and mixed peppers, all on skewers.

Frigrui, a Romanian kebab, is cubes of meat with bacon, onions, tomatoes, bell peppers, and mushrooms.

In all cases, the little bits of food are lined up on a bamboo or wood skewer, so they are all points on a single line. They are all collinear.

Usage In Statistics And Econometrics

In statistics, collinearity refers to a linear relationship between two explanatory variables. Two variables are perfectly collinear if there is an exact linear relationship between the two, so the correlation between them is equal to 1 or 1. That is, X

} is relatively small.

The concept of lateral collinearity expands on this traditional view, and refers to collinearity between explanatory and criteria variables.

Recommended Reading: Eoc Fsa Warm Ups Algebra 1 Answers

Application Of Collinear Points And Non

• Collinear points: Suppose in a series of individual items located in a straight line. For example, lets take a row of eggs in a carton when each egg placed in a single line or few numbers of students seated in a long classroom table is called Collinear points. The objects should be placed in such a way that you should be able to draw a straight line through them.
• You can also see Collinear points in various food items available worldwide such as Dango in Japan, which are sweet little dumplings arranged in three or five skewers, or a South African dish called Sosatie, which is little cubes of Lamb or Mutton with dried apricots, red onions, mixed peppers, etc. arranged on a skewer.
• Non-collinear Points: These are points that do not lie on the same plane. Suppose you have multiple sushi rolls placed on different skewers. To have collinearity, all the points should lie on the same line. Since they are all located on different skewers, a line cannot be formed using all the points together, and hence, it will form Non-collinear points. Imagine a picture of a right angle with two different points labeled L and R. If L is forming hypotenuse and R is forming the base then, both are Non-collinear to each other.

What Are Collinear Points In Maths

From the above definition, it is clear that the points which lie on the same line are collinear points. To understand this concept clearly, consider the below figure and try to categorize the collinear and non-collinear points.

In the above figure, the set of collinear points are , , , and . The remaining points are said to be non-collinear, i.e. , and so on.

You May Like: Unit 1 Geometry Basics Test Answer Key

Area Of Triangle Method

Three points are collinear if the value of the area of the triangle formed by the three points is zero.

Substitute the coordinates of the given three points in the area of triangle formula. If the result for the area of the triangle is zero, then the given points are said to be collinear.

Formula for area of a triangle formed by three points is

Let us substitute the coordinates of the above three points R, S and T in the determinant formula above for the area of a triangle to check if the answer is zero.

\= \= \= 0

Since the result for the area of the triangle is zero, therefore R , S and T are collinear points.

What Are Lines And Angles

Lines: Lines are the figures that are made up of infinite points extending towards both directions. Lines are usually straight and have considerable width and depth. Lines can be perpendicular, parallel, intersecting, transversal, etc. Lines are further categorized as line segments and rays.

Angle: An angle is a figure which is formed by two rays that are meeting at a common end-point. The relation between two angles can either be Supplementary, Complementary, Adjacent and Vertically Opposite. An Angle can be categorized as Acute Angle, Right Angle, Obtuse Angle , straight Angle .

Recommended Reading: Holt Geometry Lesson 4.5 Practice B Answers

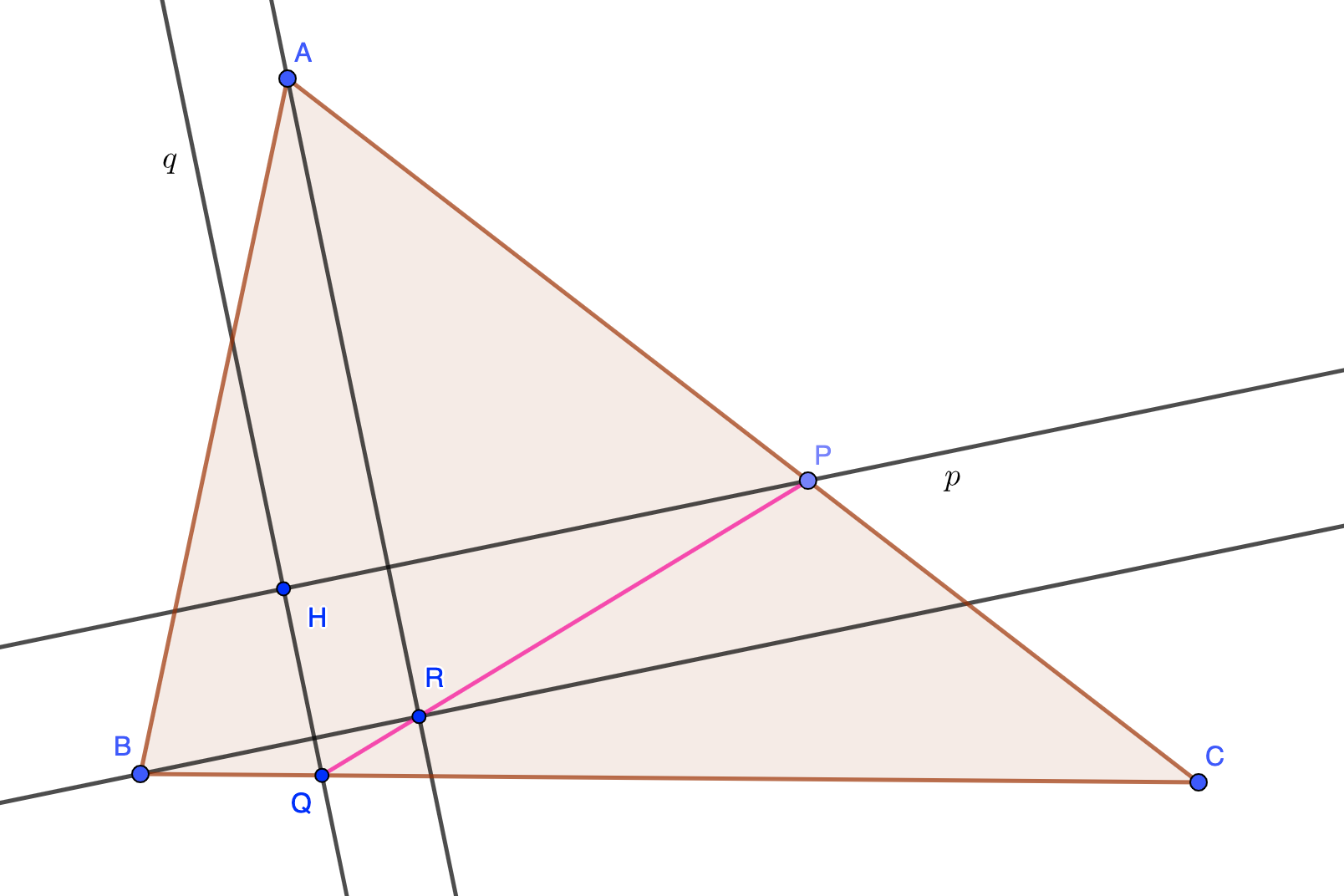
Examples On Collinear Points

Collinear Points And Non

• Collinear Points: Collinear points are the points that lie on the same plane either in the same line, apart, or from a ray. Co: Together, and linear: line.
• Non-collinear Points: These are the set of points that do not lie on the same line.
• Collinearity in Geometry: Collinearity in Geometry is the property of the points lying on a single line. In Euclidean Geometry, this relation is visualized by the points lying in a row or a straight line. However, in geometry, a line is typically a primitive , so such visualizations will not be considered appropriate. Geometry offers a model of how these points, lines, and objects are in relation to each other and how collinearity can be interpreted between them. In Spherical Geometry, where a model of a circle represents lines, the sets of Collinear points will lie on the same great circle and do not lie on a straight line.

Don’t Miss: Lesson 9.5 Geometry Answers

Collinearity Of Points Whose Pairwise Distances Are Given

A set of at least three distinct points is called straight, meaning all the points are collinear, if and only if, for every three of those points A, B, and C, the following determinant of a CayleyMenger determinant is zero meaning the distance between A and B, etc.):

det = 0. 0& d^& d^& 1\\d^& 0& d^& 1\\d^& d^& 0& 1\\1& 1& 1& 0\end}=0.}

This determinant is, by Heron’s formula, equal to 16 times the square of the area of a triangle with side lengths d, d, and d so checking if this determinant equals zero is equivalent to checking whether the triangle with vertices A, B, and C has zero area .

Equivalently, a set of at least three distinct points are collinear if and only if, for every three of those points A, B, and C with d greater than or equal to each of d and d, the triangle inequalityd d + d holds with equality.

Collinear Points & Non

Collinear points : Three or more points lying on the same line are called collinear points.

Non-collinear points : Three or more points are not lying on the same line are called non-collinear points.

Examples

Let us considered three points P, Q and R in a plane. If we draw a linel passing through two points P & Q , then there are two possibilities

a) Point R lies on the line l

b) Point R does not lie on the line l

If a point R lies on the line l then points P , Q & R lie on the same line and are said to be collinear points.

If a point R does not lie on the line l , then points P, Q and R do not lie on the same line and are said to be non- collinear points.

Read Also: Segment And Angle Addition Worksheet

What Is Collinear Points In Geometry

We all have struggled with maths once in our life. Even if you are good at the subject, you will come across various questions either at your school level or any entrance examination where you may have needed some help to understand the concept. For the students preparing for their upcoming examination for maths, Geometry is a very important topic. This topic usually takes up a big chunk in the total syllabus, but geometry can be quite scoring once grasped.

A student should have a better understanding of Geometry because it is not only limited to your subject but also applies to real-life situations. Geometry is all about shapes, which include lines, curves, rays, etc. To understand Collinear Points in Geometry first, we need to understand the basics of lines and angles. So, without wasting any time, lets get started.

Definition Of Point In Math:

A point is that which has no part. It has only one position. It does not have dimensions like length, breadth or height

Consider the step from points to solid

Point Line Surface Solids

In the above figures, the first figure is Point. It has no dimension. If it further add one dimension length then it will be line segment. If further add one more dimension breadth then it will have two dimension which is rectangle . Now add one more dimension height then it has three dimension which is cuboid .

Also Check: Segment Addition Postulate And Midpoint Worksheet