Friday, April 19, 2024
Math

How To Solve Combination Math Problems

By Kira S
0
0

Don't Miss

Generating Permutations And Combinations

Permutation and Combination Class 11 | Permutations Combinations | Chapter 7 Maths CBSE
  • It’s occasionally useful to actually generate all of the permutations/combinations, not just count them.
  • e.g. you want to do write code to search for a perm/comb that satisfies some condition.
  • e.g. you want to write an automated test for code that should be able to handle input in any order.
  • We should first decide on a way to order permutations. Then we can generate them in that order, and be sure we found them all.
  • We will order them based on lexicographic order.
  • which is a fancy way to say dictionary order.
  • We will say that a permutation \ is less than \ if either:
  • \ is less than \.
  • \ and \ is less than \.
  • Two permutations are equal if all elements are the same.
  • A permutation \ is greater than \ if \ is less than \.
  • For example, if we are permuting the letters \, then the permutation \ is less than \.
  • Aside: lexicographic ordering comes up in weird places. Sometimes you just need to know that some objects can be ordered so a proof/algorithm works out. Often you can just say lexicographic ordering and you’re done.
  • The following algorithm will generate all permutations of elements of a set, in lexicographic order:
    procedure all_permutations    if length == 1        return the element as a length-one permutation    else        all_perm =         for each x in S.in_sorted_order            S1 = S -             for each P in all_permutations                all_perm +=  + P        return all_perm
  • For a one-element set, , it returns that element in its only order:

    • Multiplication Combinations Teaching Resources

    Step 1: Our set, in this case, is the total number of problems given. The size of this set is 10. Step 2: The size of our combination will be 8 because that’s how many problems you are

    • Figure out math tasks

      Math can be tough, but with a little practice, anyone can master it!

    • Clear up mathematic problems

      Having trouble with math? Don’t worry, our experts can help clear up any confusion and get you on the right track.

    • Writing Versatility

      No matter what you’re writing, good writing is always about engaging your audience and communicating your message clearly.

    • Solve mathematic question

      Solving math equations can be challenging, but it’s also a great way to improve your problem-solving skills.

    • Determine math questions

      You can use math to determine all sorts of things, like how much money you’ll need to save for a rainy day.

    • To solve a math equation, you need to decide what operation to perform on each side of the equation.

    Understand The Mathematical Notation Of Combinations

    Although different combination probability problems require different mathematical formulas, they contain the same key concepts and variables. The important terms and notations to understand are:

    • Factorial notation: Factorial notation is when you write an exclamation point immediately next to a number. This is a mathematical symbol that represents the value you get when you multiply the number by each integer smaller than it down to one, successively. For example, “3!” is the equivalent of writing 3 x 2 x 1.

    • Pascal’s triangle: Using Pascal’s triangle can help you find some combination solutions quickly. Pascal’s triangle is an array of numbers starting with one on the top row and filling out each successive row first with two numbers, then three numbers and so on to create a triangle shape. Each number in the triangle is equal to the sum of the number above it and to the left and the number above it and to the right.

    • Variable n: The variable n represents the number of options for each selection in the combination. For example, a lock with three digits, each of which can be 0 to 9, has an n value of 10 because there are 10 possible digits for each spot in the combination.

    • Variable r: The variable r represents the number of times you make a selection from the potential elements. For the example combination, r would be equal to three because there are three digits in the lock permutation.

    Related: Factorials: What Are They, How To Calculate Them and Examples

    Don’t Miss: What Is Elasticity In Physics

    Relationship Between Permutations And Combinations

    Permutation and combination formulas and concepts have a lot of similarities. Suppose that you have n different objects. You have to determine the number of unique r-selections which can be made from this group of n objects. Think of a group of n people you have to find the number of unique sub-groups of size r, which can be created from this group.

    The number of permutations of size r will be \. In the list of \ permutations, each unique selection will be counted r! times, because the objects in an r-selection can be permuted amongst themselves in \ ways. Thus, the number of unique combinations can be \.

    Permutation And Combination Calculator

    Solving Systems of Equations Word Problems

    Permutations and combinations are part of a branch of mathematics called combinatorics, which involves studying finite, discrete structures. Permutations are specific selections of elements within a set where the order in which the elements are arranged is important, while combinations involve the selection of elements without regard for order. A typical combination lock for example, should technically be called a permutation lock by mathematical standards, since the order of the numbers entered is important 1-2-9 is not the same as 2-9-1, whereas for a combination, any order of those three numbers would suffice. There are different types of permutations and combinations, but the calculator above only considers the case without replacement, also referred to as without repetition. This means that for the example of the combination lock above, this calculator does not compute the case where the combination lock can have repeated values, for example, 3-3-3.

    Don’t Miss: Multiple View Geometry In Computer Vision Book

    Number Of Combinations With Repetition

    A k–combination with repetitions, or k–multicombination, or multisubset of size k from a set S of size n is given by a set of k not necessarily distinct elements of S, where order is not taken into account: two sequences define the same multiset if one can be obtained from the other by permuting the terms. In other words, it is a sample of k elements from a set of n elements allowing for duplicates but disregarding different orderings . Associate an index to each element of S and think of the elements of S as types of objects, then we can let x i } denote the number of elements of type i in a multisubset. The number of multisubsets of size k is then the number of nonnegative integer solutions of the Diophantine equation:

    Permutations = More Possibilities

    You always have fewer combinations than permutations, and heres why:Take the numbers 1, 2, 3, 4. If you want to know how many ways you can select 3 items where the order doesnt matter , you can pick:

    However, if you want permutations (where the order does matter, the same set has 24 different possibilities. Just take the first set of numbers listed above and think of the ways you can order it.

    There are six ways to order the numbers, which means there are 4 x 6 ways to order the set of four numbers.

    Repetitions are just repeating numbers. They become important when it comes to choosing the right formula.

    • 123 has no repetitions .
    • 223 has the number 2 repeated.

    Allowing repetition depends on your situation. For example:

    • Combination locks can have any number in any position , so repetitions are allowed. The number 9 appears twice here.
    • Lottery numbers dont allow repetition. The same number wont appear twice in the same ticket. For example, you can pick numbers 67, 76, and 99. But you cant choose 67, 67, and 67 as your winning ticket.

    Logic should tell you if repetitions are allowed. For example, if youre dealing with items that arent going to be replaced , then youre looking at no repetitions allowed.

    You May Like: What Does Converse Mean In Geometry

    What Is A Combination

    A combination is a mathematical technique that determines the number of possible arrangements in a collection of items where the order of the selection does not matter. In combinations, you can select the items in any order.

    Combinations can be confused with permutations. However, in permutations, the order of the selected items is essential. For example, the arrangements ab and ba are equal in combinations , while in permutations, the arrangements are different.

    Combinations are studied in combinatorics but are also used in different disciplines, including mathematics and finance.

    Ti 89 Combinations: Steps:

    Permutation Word Problems Explained the Easy Way

    Example problem: If there are 5 people, Barb, Sue, Jan, Jim, and Rob, and only three will be chosen for the new Parent Teacher Association, how many combinations are possible for the committee?

    Step 1: Press the HOME screen on the calculator.

    Step 2: Press the CATALOG key.

    Step 3: Press ALPHA 6. This selects the letter n and brings you to the ns in the list. If it doesnt, try pressing ALPHA 6 again.

    Step 4: Find nCr(. Press ENTER.

    Step 5: Press 5. This is the number of possible people, or n.

    Step 6: Press the comma, then 3. This is the number of people we need to choose, or r.

    Step 7: Press ). The entry on your calculator should now read nCr. Press ENTER. This returns you result. There are 10 possible ways this committee can be chosen.

    Tip: Instead of hitting the ALPHA and 6 keys, use the scroll button to scroll through the menu.Tip: Want to check your answer? Use our free, online combinations calculator and permutations calculator to check your work.

    Don’t Miss: Glencoe Mcgraw Hill Geometry Textbook

    Combinations Word Problems Examples

    Example 1 :

    Kabaddi coach has 14 players ready to play. How many different teams of 7 players could the coach put on the court?

    Solution :

    Number of ways of selecting 7 players out of 14 players

    = 14C7

    = /7! 7!

    = / 7!

    = 3432

    Example 2 :

    There are 15 persons in a party and if each 2 of them shakes hands with each other, how many handshakes happen in the party?

    Solution :

    Before going to look into the solution of this problem, let us create a model.

    Number of hand shakes = n /2

    Here we divide n by 2, because of avoiding repetition.

    Number of persons in a party = 15

    Number of hand shakes can be made = 15 / 2

    = 15 /2

    Hence the required number of chords can be drawn is 190.

    Example 4 :

    In a parking lot one hundred , one year old cars, are parked. Out of them five are to be chosen at random for to check its pollution devices. How many different set of five cars can be chosen?

    Solution :

    In the given question, we have a word “different set of five cars”.

    So we have to use the concept combination.

    Number of ways of choosing 5 cars = 100C5

    Hence the answer is 100C5.

    Example 5 :

    How many ways can a team of 3 boys, 2 girls and 1 transgender be selected from 5 boys, 4 girls and 2 transgenders?

    Solution :

    What Is Combination In Math

    An arrangement of objects in which the order is not important is called acombination. This is different frompermutation where the order matters. For example,suppose we are arranging the letters A, B and C. In a permutation, the arrangementABC and ACB are different. But, in a combination, the arrangements ABC and ACB are thesame because the order is not important.

    What Is The Combination Formula?

    The number of combinations of n things taken r at a time is written as C.

    The following diagram shows the formula for combination. Scroll down the page for moreexamples and solutions on how to use the combination formula.

    If you are not familiar with the n! then have a look the factorial lesson

    How To Use The Combination Formula To Solve Word Problems?

    Example:In how many ways can a coach choose three swimmers from among five swimmers?

    Solution:There are 5 swimmers to be taken 3 at a time.Using the formula:

    The coach can choose the swimmers in 10 ways.

    Example:Six friends want to play enough games of chess to be sure every one plays everyone else. Howmany games will they have to play?

    Solution:There are 6 players to be taken 2 at a time.Using the formula:

    They will need to play 15 games.

    Example:In a lottery, each ticket has 5 one-digit numbers 0-9 on it. a) You win if your ticket has the digits in any order. What are your changes of winning?b) You would win only if your ticket has the digits in the required order. What are yourchances of winning?

    a) Using the formula:

    Examples:

    Don’t Miss: What Courses Are Required For Psychology Major

    Permutations With Identical Objects

    • There are many problems similar to the basic combination/permutation ones.
    • The basic approach is: how can you make it look like a problem you know how to solve? When you do, how much did over-/undercount by?
  • Example: How many ways are there to permute the letters of the word \?
  • There would be \ ways to permute \ since all of the letters are different.
  • How do we deal with the repeated P? Let’s pretend they’re different: \.
  • Now there are \ ways, but we counted both of these, but in the original problem they should only be counted once: \
  • In fact, we counted every permutation twice: with each possible ordering of the Ps.
  • Real solution: \.
  • Example : How many ways are there to permute the letters of the word \?
  • Let’s first decide where to put the Ps, in \\) ways.
  • Then in the remaining 3 positions, permute the remaining 3 elements.
  • Final answer: \
  • Theorem: There are \ ways to permute \ objects where \ are idential are different).

    Proof idea: Exactly as the previous example, with \ and \.

  • Theorem: Suppose we have \ items, where there are \ that are identical. The number of ways to permute them is \ We will demand that \ for the proof, but obviously we don’t really need to count one-of-a-kind items to get the right answer, since \.

    Proof: As before, first select positions for the \ identical items in \\) ways. Then place the \ items in \\) ways, and so on. The total number of ways to arrange the items is \

  • There are 104 cards in total, but the pair of each card is identical .

    • Example Combination Without Repetition

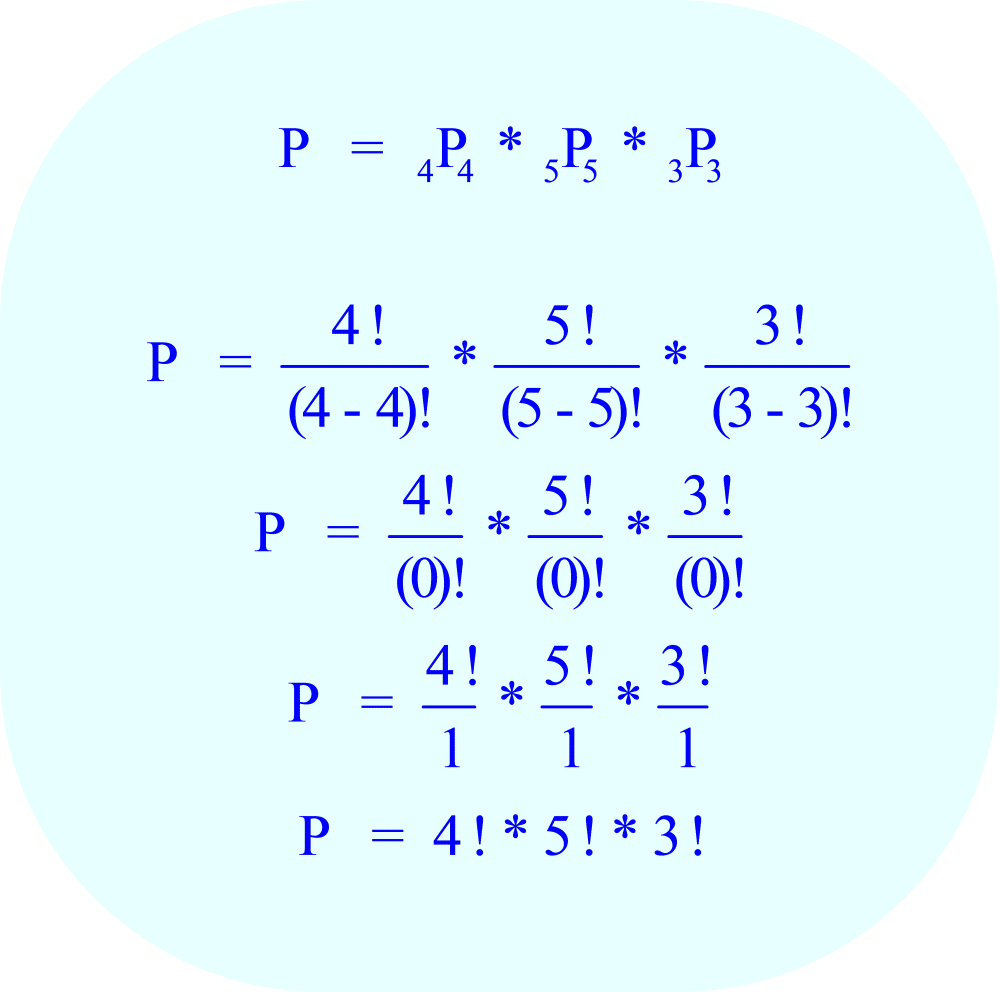
    Scheduling and Permutations

    While the previous formula treats drawing the same three marbles in a different order as different results, in a combination they are the same. Dividing by the factorial of the number of selections made allows you to remove duplicates and find your correct result.

    In the marble example, since each combination of three marbles can happen in one of six permutations, you divide 60 by 6 to discover there are 10 combinations without repetition.

    You can also solve for the number of combinations without repetition using Pascal’s triangle. Treating the top row of the triangle as row zero, count down to the row matching the number of options for each element, then count over in that row equal to the number of selections to find the result.

    Total combinations = 5! / !) = 5! / = 120 / = 120 / 12 = 10

    Related: Types of Probability: Definition and Examples

    Read Also: Discovering Geometry Chapter 3 Answers

    What If I Dont Know Which Formula To Use

    Most of the time, you arent told whether you should use the permutation formula or the combination formula. Part of problem solving involves figuring this out on your own. The following examples show you how to do this.

    Example problem #1:Five bingo numbers are being picked from a ball containing 100 bingo numbers. How many possible ways are there for picking different numbers?

    Step 1: Figure out if you have permutations or combinations. Order doesnt matter in Bingo. Or for that matter, most lottery games. As order doesnt matter, its a combination.

    Step 2: Put your numbers into the formula. The number of items is n. And k is the number of items you want to put in order. You have 100 Bingo numbers and are picking 5 at a time, so:Step 3: Solve:Thats it!Example problem #2.Five people are being selected for president, vice president, CEO, and secretary. The president will be chosen first, followed by the other three positions. How many different ways can the positions be filled?

    Step 1: Figure out if you have permutations or combinations. You cant just throw people into these positions They are selected in a particular order for particular jobs. Therefore, its a permutations problem.

    Step 2: Put your numbers into the formula. There are five people who you can put on the committee. Only four positions are available. Therefore n is 5, and k is 4:Step 3: Solve:

    Identify Your Style Of Combination

    In order to apply the correct formula when calculating your combination, it’s important to identify the type of calculation you are performing. The first key point is whether you are calculating a permutation or a combination. Then, you may identify if the same value can repeat during the combination. This creates four calculation types, one for each potential pairing of combination or permutation and repetition or no repetition.

    Don’t Miss: Geometry Dash Hexagon Force Scratch

    What Is A Combination In Math

    A combination is a set of elements created under a specific set of conditions and restrictions. The combination may consist entirely of unique elements or include repeated elements, and the combination may require those elements to be in a specific order or simply to have all the correct elements present.

    In mathematics, understanding the parameters of a combination allows you to calculate the different number of possible combinations that meet those requirements and, as a result, the probability of a specific outcome occurring.

    Related: What are Mathematical Combinations and How To Calculate Them

    Calculates The Number Of Combinations Of N Things Taken R At A Time

    Solving a more complicated equation | Linear equations | Algebra I | Khan Academy

    number of things n number to be taken r combinations nCr

    \ _nC_r=\binom=}\\\ _nC_r=_nP_r}}\\\)
    2023/01/19 01:46 20 years old level / High-school/ University/ Grad student / Useful /

    Purpose of use
    2022/12/27 07:55 60 years old level or over / A retired person / Very /

    Purpose of use
    To calculate the number of combinations in a Project Euler problem in order to get the magnitude of the number of combinations my solution would have to deal with. 8 trillion is a big number exception in Washington DC.
    2022/12/20 20:55 Under 20 years old / High-school/ University/ Grad student / Useful /

    Purpose of use
    For exams in school, good
    2022/11/29 22:26 40 years old level / An engineer / Useful /

    Purpose of use
    solving a recreational math problem
    2022/10/16 02:41 20 years old level / An engineer / Very /

    Purpose of use
    To calculate number of ways to make 2 football teams of 11 players each, from a group of 22 people
    2022/09/02 03:56 60 years old level or over / A retired person / Very /

    Purpose of use
    2022/08/22 02:46 20 years old level / Self-employed people / Useful /

    Purpose of use
    Calculating the number of possible recipes of cooking in a game’s cooking system.
    2022/08/09 03:49 30 years old level / Self-employed people / Very /

    Purpose of use
    2022/06/02 12:47 Under 20 years old / High-school/ University/ Grad student / Very /

    Purpose of use
    calculator used for Algebra 2 class homework
    2022/05/16 07:45 20 years old level / High-school/ University/ Grad student / Very /

    Purpose of use

    Recommended Reading: What Are The Different Types Of Psychology

    Previous articleWhat Grade Do You Learn Pre Algebra
    Next articleHow Technology Is Shaped By Physics

    More articles

    Popular Articles

    © 2021 Tutordale.com
    Contact us: contact@tutordale.com

    About Us

    Popular Category

    Editor Picks