How To Find Speed In Physics

Average Vs Instantaneous Speed

The examples so far calculate average speed: how far something travels over a period of time.

But speed can change as time goes by. A car can go faster and slower, maybe even stop at lights.

So there is also instantaneous speed: the speed at an instant in time. We can try to measure it by using a very short span of time .

How To Find Initial Velocity

If you want to calculate intitial velocity instantly, then all you need to plug-in the values into the above initial velocity calculator. And, if want to do it manually, then use the below initial velocity formula:

Formula For Initial Velocity:

Initial velocity = final velocity

vi = vf at

Read on!

• First of all, you have to figure out which of the displacement , final velocity , acceleration , and the time you have to solve for initial velocity
• If you have Vf, A, and T, then you ought to use Vi = Vf AT
• If you have S, Vf, and T, then you ought to use Vi = 2 Vf
• If you have S, Vf, and A, then you ought to use Vi = Square root of
• If you have S, A, and T, then you ought to use Vi =

Example :

A body traveling from 36s and now its speed is 180m/s with an acceleration of 4ms-2. Calculate the initial velocity of the body?

Solution:

S = UT + 1/2 AT^2

V^2 = U^2 + 2AS

Read on!

• First of all, find out which of the initial velocity , acceleration time , and displacement , you have to solve for final velocity.
• If you have U, A and T, then you ought to use V = U + AT
• If you have S, U, and T, then you ought to try V = 2 U
• If you have S, U, and A, then you ought to use V = Square root
• If you have S, A, and T, then you ought to use V = +

Example :

A body starts from rest and continues to travel from 40s with an acceleration of 8ms-2.Find the final velocity of the body?Solution:

vf =320ms-1

What Is Speed In Physics

The definition of Speed in Physics is the distance covered by an object in unit time. In other words, the rate at which the object is moving is called speed. Unit time may be a second, an hour, a day, or a year. It tells us how fast or slow an object is moving. Speed is the scalar Quantity. SI unit of speed is m/s. Examples of Speed are given below in the post.

Don’t Miss: Segment Addition Postulate Practice Answer Key

How To Calculate Average Speed

To calculate the average speed of an object, you must know the total distance an object travels and the total elapsed time of its whole journey.

The distance/speed/time triangle is handy for calculating this and two other scalar quantities :

The three parts in the triangle are set up in their correct positions mathematically:

Average speed is especially useful because it takes into account the reality of an event, rather than assuming something or someone is moving at a constant speed.

The porpoise could have started slowly, sped up, paused to play, and continued. That three-toed sloth may have stopped for a moment to catch its breath before hurrying onward. You might have to make numerous stops when walking a dog, but in all three cases, you can easily calculate average speed by dividing the total distance traveled by total elapsed time.

Difference Between Speed And Velocity

Speed denotes only how fast an object is moving, whereas velocity describes both how fast and in which direction the object is moving. If a car is said to travel at 60;km/h, its speed has been specified. However, if the car is said to move at 60;km/h to the north, its velocity has now been specified.

The big difference can be discerned when considering movement around a circle. When something moves in a circular path and returns to its starting point, its average velocity is zero, but its average speed is found by dividing the circumference of the circle by the time taken to move around the circle. This is because the average velocity is calculated by considering only the displacement between the starting and end points, whereas the average speed considers only the total distance travelled.

Recommended Reading: Geometry Segment Addition Postulate Worksheet

Things Move Some Faster Than Others

In physics, we are concerned both with objects at rest and objects in motion . Speed is an important measure of the quantity and character of motion. In math classes, we often refer to speed as rate, or rate of travel. Speed is defined as the distance traveled divided by the time it takes

In what follows, we’ll be working on linear speed, speed of an object traveling in a straight line, not along a curve.

$$\text = \frac}}$$

$$s = \frac$$

First: an Algebra tuneup

It’s worth pausing here to note that physics is full of three-variable equations like this, and much of the work you’ll do to model and solve physical problems will consist of rearranging and solving equations like this with simple algebra. Here are the three rearrangements of the speed equation and how they’re obtained:

A handy trick

There’s a useful trick to these kinds of rearrangements if your algebra is weak or rusty, the “magic triangle” . You can use it to find the rearrangements of any three-variable equation. Just set up the equation in the triangle in a form you know – note the similarity of the arrangement in the left-most triangle: speed equals distance over time. Then to solve for one of the variables, cover that variable with a finger and read off the solution. The middle triangle: distance = speed times time. The right triangle: time = distance over speed.

What Causes A Change In Velocity

Experts depicts that forces are something that affect how objects move they may cause motion, also, they may stop, slow or even change the direction of motion of an object . As force cause changes in the speed or direction of an object, it is said to be that forces causes changes in velocity. Remember that acceleration is said to be change in velocity.

Don’t Miss: Math Caching

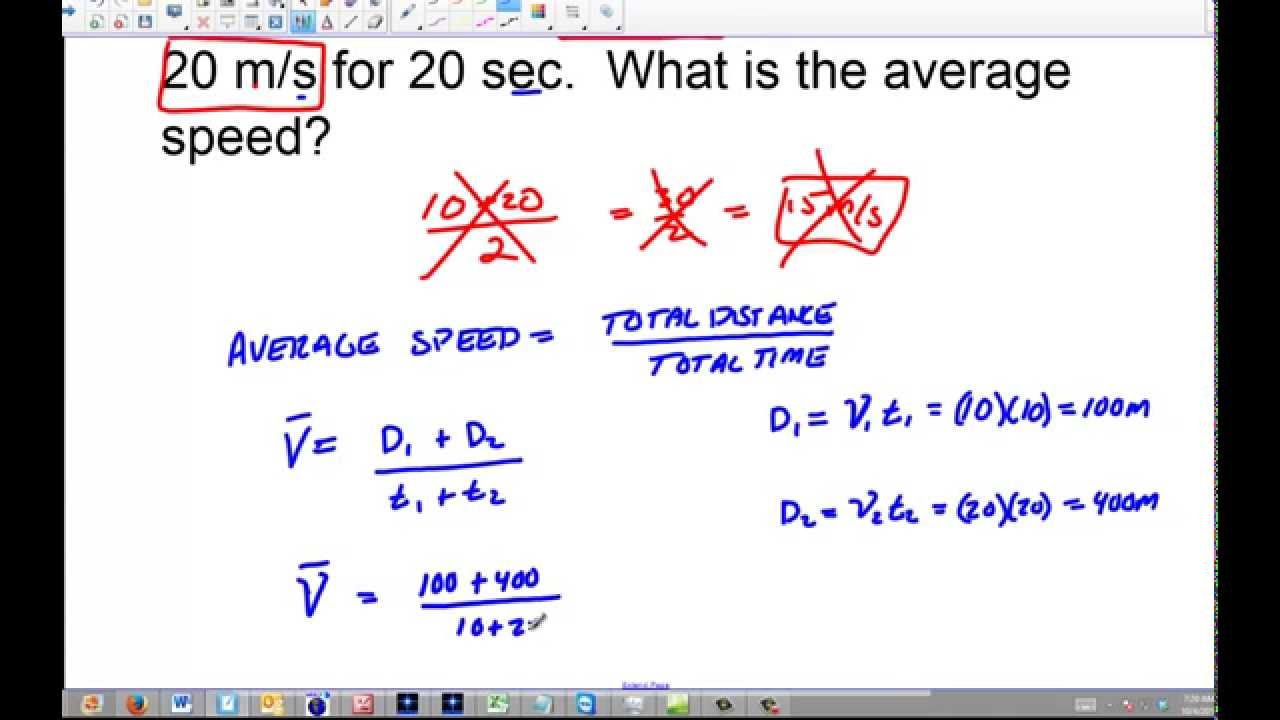
Example 1 Calculating Average Speed

It takes 1:50 to cycle from Sharon, MA to Providence, RI, a distance of 29.3 miles. Calculate the average speed of such a trip in mi./h

Solution : First we need to convert 1 hour + 50 min. to hours. 50 minutes is 5/6 hour or 0.833 hours, so 1:50 = 1.833 hours.

Now the speed average speed is just:

$$ \begin s &= \frac = \frac \\&= \bf15.9 \: \frac \end$$

We should probably round that to 15.9 or 16 mi./h because we only know the distance to the tenths place it’s just good practice.

Note: Once in a while you’ll see mi./h written as mi.h-1. It’s written that way because printed text like what you’re reading now looks best on one line, and because it’s poor practice to write fractions with a slash / on the same line it’s a good way to lose track of units.

Solved Example Of Relative Speed

Question:Two vehicles are travelling from the same location at the speed of 6 km/hr and 4 km/hr respectively. Calculate the distance between the vehicles after 10 minutes given that both vehicles are travelling in the same direction.

Solution:The relative speed of the vehicles when they move in the same direction

= km/hr

Total time taken = 10 minutes

Therefore distance travelled = speed × time= km= 1/3 × 1000 m= 333.3 m

Therefore, the distance between the vehicles after 10 minutes is 333.3 m given that both vehicles are travelling in the same direction.

Stay tuned with BYJUS to learn more interesting topics and related concepts like relative velocity, relative speed formula, etc. with the help of interactive video lessons.

Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!

Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz

Recommended Reading: Geometry Basics Segment Addition Postulate Answer Key

Difference Between Uniform And Non Uniform Speed

Uniform Speed:

The body has uniform speed if it covers equal distances in equal intervals of time however short the interval may be.

In the equation, S=v t ;v is the average speed of a body during time t. It is because the speed of the body may be changing during the time interval t. However, if the speed of a body does not vary and has the same value then the body is said to possess uniform speed.

Non Uniform Speed:

A body does not have uniform speed if it does not cover the equal distance with an equal interval of time.Related Topics:

Some Specific Cases Of Relative Speed

CASE 1 : Boats & Streams

Let the Speed of boat in still water = x

Speed of stream = y

As it is previously discussed that in questions where two bodies with different Speeds are concerned, the concept of relative speed should be used. Here the stream can be assumed to be the stationary body and the Speed of boat relative to the Speed of the stream can be taken. Using the concept of relative Speed, one can now have the situation where the stream is stationary and only the boat is moving at a speed determined by the direction of the boat relative to the stream.

Example 3:

Gita rows a boat at a speed of 15 kmph upstream and 20 kmph downstream. Find the Speed with which Gita rows the boat in still water and also find the Speed of the stream.

Solution:Given that upstream Speed = 15 kmph

Downstream Speed = 20 kmph

Speed of Gita in still water = x = )/2= /2 = 35/2

Speed of stream =y = )/2= /2 = 5/2.

Example 4:

The Speed of Narmada river is 5 kmph. A stationary body is placed in the river. Find the Time taken by the floating body to reach a stone which is 10 km downstream from the point where it is now?

Solution:

Speed=Distance/Time.

So, Time taken to reach 10 km = 10/5 = 2 hours.

Example 5:

A man rows 135 km upstream in 2.7 hours. He rows the same distance downstream in 2.5 hours. However, for downstream, he reduces his Speed by 9%, while Speed of the current gets reduced by 20%. Find the Speed of the man.

x= The speed of boat and

y= The Speed of stream

Example 6:

Solution:

Also Check: Exponential Growth And Decay Common Core Algebra 1 Homework Answer Key

Speed Distance Time &calculus

This section is entirely optional, but read on if you know something about calculus and you’d like to learn about its role in physics. By the way, if you don’t know anything about it, don’t worry. Calculus really isn’t a huge mystery, and it will make perfect sense when you do learn it.

Because the first derivative of a function is its slope, the first derivative of the position with respect to time is the speed.

Speed is the first derivative of position with respect to time.

$$s = \frac$$

Now if we view the integral as a sum, then the net distance traveled, provided we have some functional form for the speed, is just the integral of that function between two times, t1 and t2

Distance is the definite integral of speed, s over the time range t1 to t2.

$$x = \int_^\:s\,dt$$

There are many other derivative and integral relationships in physics. Any rate is the derivative of some underlying function, and any time a quantity that can be represented as a continuous function is summed that’s an integral.

Using The Standard Speed Equation

Don’t Miss: Eoc Fsa Warm Ups Algebra 1 Answers

Speed Is The Slope Of A Distance Vs Time Graph

When distance traveled is plotted vs. elapsed time, the slope of the graph is the average speed.

Often in math we get the impression that units and even the relative scales of the y and x axes must be the same. It isn’t so. In this graph, distance in meters divided by time in seconds gives speed in m/s, an acceptable unit.

The graphs below illustrate a few different kinds of d vs. t graphs you might encounter. You should learn to interpret graphs like these.

Interpreting position vs. time graphs

Here are a few examples of position vs. time graphs for you to practice interpreting. Explanations for each chunk of time are given below each graph, and you can roll-over or tap the graph to see another version of the explanation. Make sure to reason each out for yourself before looking at the explanations.

1. Between t=0 and t1 the object is moving in the +x direction at a constant speed, given by the slope of the line, $\Delta x / \Delta t.$ Between t1 and t2 the particle is not moving, and remains at position x2. The slope of the horizontal line across this region is zero, so the speed is zero. Between t2 and t3, the object travels at constant velocity in the -x direction. Finally, after t3, the object is moving in the +x direction, but not at constant velocity. The slope of the curved section decreases over time, so the particle is slowing down as it moves.

What Is Relative Speed

We can define relative speed as the speed of a moving body with respect to another. When two bodies are moving in the same direction, the relative speed is computed by their difference. But when to bodies are moving in the opposite direction, the relative speed is calculated by adding the speed of both the bodies.

The difference between relative speed and relative velocity is that relative speed is the scalar quantity whereas relative velocity is the vector quantity.

You May Like: Geometry Segment Addition Postulate Worksheet

How To Calculate Speed In Physics

We can calculate Speed by using Formula of Speed in Physics:

Here S is the distance covered by the object, V is its speed, and t is the time taken by it. Distance is a scalar; therefore speed is also a scalar quantity.SI unit of speed is meter per second, other units like kilometer per hour, miles per hour, feet per second are also used.

See Also: Difference between Distance and Displacement

Average & Instantaneous Speed

If you drive from Salida, CO to Denver, CO, you’ll cover a distance of about 150 miles , and it will take you about 3 hours. What you can calculate from that is average speed:

$$s = \frac = \frac = \bf 50 \frac$$

Pro tip: in science, we don’t really use the common abbreviation “mph” for “miles per hour.” We use the fraction

$$\frac$$

It’s important to notice that what we’ve actually calculated is an average speed. In fact, on that trip, there are several stop signs, mountain passes and other places where speed can be faster or slower than the average. We don’t know anything about any of those details when we calculate average speed, just the total time and distance.

Instantaneous speed, the speed of an object, like a car, at any one instant in time is harder to calculate , but we can measure instantaneous speed at any time in a car by looking at the “speed-o-meter.”

Often we put a bar over a quantity to denote that it is an average, so average speed is sometimes written as ;s.

Recommended Reading: Introduction To Exponential Functions Common Core Algebra 1 Homework Answer Key

How Do You Find Final Velocity With Calculator

All you need to do the following:

• First of all, you have to hit the acceleration tab
• Very next, you have to choose the final velocity option from the drop-down menu of final velocity calculator
• Then, you have to enter the value of the initial velocity into the designated box
• Right after, you have to enter the value of acceleration into the given box
• Finally, you have to enter the value of the time into the designated field, then, hit the calculate button, the calculator for final velocity will instantly calculate final velocity for the given inputs