How Do You Do Percentages In Math

How Do You Do Math Percentage Problems

To calculate percentages, convert the percentage to a decimal and multiply it by the number in the problem. For example, to find 40 percent of 50, change it to 0.40 times 50, which gives you the result of 20.

There are several methods for solving a percentage problem. For example, 100 percent of a number is the same number. So 100 percent of 50 is 50. When you double the percentage to 200, you can just double the number as well, which means that 200 percent of 50 is 100.

Do the same when reducing a number. To find 50 percent of 50, solve the problem by simply cutting the number in half. Therefore 50 percent of 50 is 25.

When you have an uncommon percentage, such as finding 4 percent of 200, you can rearrange the numbers to find the same result. This means that instead of finding 4 percent of 200, you can find 200 percent of four, which would be four times two, or eight. This method serves as a faster way to solve a seemingly complex percentage problem without having to do difficult multiplication.

For the inverse, or finding what percentage one number is of another, divide the first number by the second. If you’ve scored 20 out of 25 on a quiz and want to know your score as a percentage, divide 20 by 25. This calculation has a result of 0.80, or 80 percent. A score of 20 out of 25 is the same as 80 percent.

Working Out Percentages Of A Whole

So far we have looked at the basics of percentages, and how to add or subtract a percentage from a whole.

Sometimes it is useful to be able to work out the percentages of a whole when you are given the numbers concerned.

For example, lets suppose that an organisation employs 9 managers, 12 administrators, 5 accountants, 3 human resource professionals, 7 cleaners and 4 catering staff. What percentage of each type of staff does it employ?

TOP TIP! Check you have a total of 100%

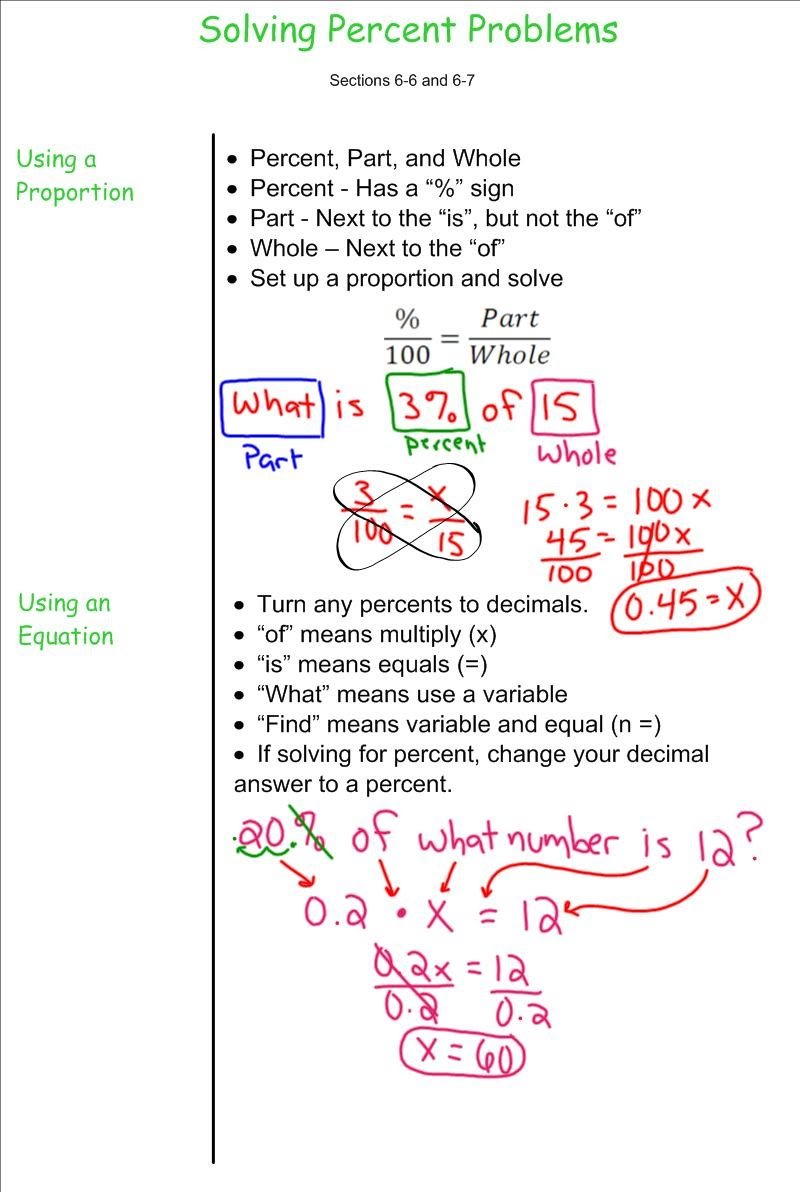
How To Calculate The Percentage What’s The Percentage Formula

Staying with our cookie examples, let’s name the three parts in our equation: the percentage of cookies – 40%, the whole pack of cookies – 20 and the part of the pack of cookies – 8. Depending on what you want to estimate, you can write three various percentage formulas:

• the equation for percentage is this: percentage = 100 * part / whole, and it answers the question “what percentage of 20 is 8”.
• the formula for a part is: part = whole * percentage / 100, and it answers “what is 40% of 20?”.
• and finally, the formula for a whole is: whole = 100 * part / percentage, and it says “what is 100% if 8 is 40%?”.

That’s technically all. You should now know how to find the percentage of a number.

Believe it or not, but knowing how to calculate percentages is essential in sports. Are you supporting any sports team? We’ve got some exciting tools for you which involve percentages. Check our winning percentage calculator to see how good the last season really was for your favorite team. Also, if you’re planning to bet on your team , visit the risk calculator to find out which option is safer.

Read Also: Eoc Fsa Warm Ups Algebra 1 Answers

Percentages As Decimals And Fractions

One percent is one hundredth of a whole. It can therefore be written as both a decimal and a fraction.

To write a percentage as a decimal, simply divide it by 100.

For example, 50% becomes 0.5, 20% becomes 0.2, 1% becomes 0.01 and so on.

We can calculate percentages using this knowledge. 50% is the same as a half, so 50% of 10 is 5, because five is half of 10 . The decimal of 50% is 0.5. So another way of finding 50% of 10 is to say 10 × 0.5, or 10 halves.

20% of 50 is the same as saying 50 × 0.2, which equals 10.

17.5% of 380 = 380 × 0.175, which equals 66.5.

Georges salary increase above was 5% of £24,000. £24,000 × 0.05 = £1,200.

The conversion from decimal to percentage is simply the reverse calculation: multiply your decimal by 100.

0.5 = 50% 0.875 = 87.5%

To write a percentage as a fraction, put the percentage value over a denominator of 100, and divide it down into its lowest possible form.

50% = 50/100 = 5/10 = ½ 30% = 30/100 = 3/10

WARNING!

It is possible to convert fractions to percentages by converting the denominator into 100.

However, it is harder to convert fractions to percentages than percentages to fractions because not every fraction has an exact decimal or percentage.

If the denominator of your fraction does not divide a whole number of times into 100, then there will not be a simple conversion. For example, 1/3, 1/6 and 1/9 do not make neat percentages .

When Is The Percentage Difference Useful And When Is It Confusing

Now it is time to dive deeper into the utility of the percentage difference as a measurement. It should come as no surprise to you that the utility of percentage difference is at its best when comparing two numbers; but this is not always the case. We should, arguably, refrain from talking about percentage difference when we mean the same value across time. We think this should be the case because in everyday life we tend to think in terms of percentage change, and not percentage difference.

For now, let’s see a couple of examples where it is useful to talk about percentage difference. Let’s say you want to compare the size of two companies in terms of their employees. In this example, the company C has 93 employees, and company B has 117. To compare the difference in size between these two companies, the percentage difference is a good measure. In this case, using the percentage difference calculator, we can see that there is a difference of 22.86%. One key feature of the percentage difference is that it would still be the same if you switch the number of employees between companies. As we have established before, percentage difference is a comparison without direction.

Don’t Miss: Exponential Growth And Decay Algebra 1 Worksheet

Distinguishing Percent And Percentage

There are some misconceptions upon the usage of the words percent and percentage. The two words have

A percent refers to a specific number.

For example;

Bernadette got 90 percent of the test questions correctly.

She got 90% in the test.

A percentage is the result when a number is multiplied by a percent. It denotes a portion and mostly described as lower or higher.

For example;

Bernadette got a high percentage in the test.

She got a percentage of 90/100 in the test.

Mostly, the word “percent” comes after a certain number and commonly these numbers are whole or counting numbers. It is not commonly used in sentences since it is always replaced by a percent symbol . The word “percentage” comes before a fraction or after an adjective .

How To Get A Percentage

Percent is another name for indicating hundredths.;Thus, 1% is one-hundredth, that means 1%=1/100=0.01.

Let’s calculate percentage using the two methods given above.;

When we have two or more values that add up to 100, then the percentage of those individual values to the total value is that number itself. For example, Sally bought tiles of three different colors for her house. The details of the purchase are given in the following table.

Also Check: Algebra 1 Eoc Answers 2015

How To Compute Percentage Greater Than 100 Percent

To calculate a percentage greater than 100 percent, simply move the decimal of the percent two spaces to the left and use the answer to multiply the number in question. You can do this to figure out what is 350 percent of 20. Moving the decimal of the percent two spaces to the left gives you 3.5. Multiplying 20 by 3.5 then gives you the answer, which is 70.

Related Articles

What Does ‘percent’ Mean

It is valuable to know the origin of the term percent if you want to truly understand how to calculate a percentage. The word percent comes from the phrase per cent. Cent is a root that means one hundred, so per cent literally means per one hundred. For example, if you know that 30 percent of the students in a school are boys, that means that there are 30 boys per one hundred students. Another way to say this is that 30 out of 100 students are boys.

Generally, the way to figure out any percentage is to multiply the number of items in question, or X, by the form of the percent. To figure out the decimal form of a percent, simply move the decimal two places to the left. For example, the decimal form of 10 percent is 0.1. Then, to calculate what 10 percent of is, say, 250 students, simply multiply the number of students by 0.1.

You May Like: Ccl4 Molecular Geometry

What Is The Percentage Of A Number

Percentage in mathematics is a number or ratio which can be represented as a fraction of 100. The term per cent originates from a Latin word per centum which means per 100. The symbol is used to denote percentage.

Similarly, percentage is sometimes denoted by an abbreviation pct. For example, we can express 50 percent as 50% or 50 pct. Percentages are written inform whole numbers, fractions or decimals. For example, 4%, 75%, 0.6%, 0.25%, 3/5% etc. are all percentages.

Percentages are part of our daily lives in the following examples:

• Discounts on commodities are represented in percentages
• Financial institutions such as banks and SACCOS express the interest charged on loans in form of percentages.
• Profits and losses are calculated in percentages
• In academics, percentages are used to evaluate the performance of students
• The values goods such cars and a piece of land changes with time. This can be represented inform of percentages.

For these reasons, possessing a knowledge on how to calculate percentages is not only helpful for you to excel in mathematics, but also to apply outside the class and solve practical problems involving percentages. This article provides a step by step tutorial on how to calculate percentages.

How Can I Work Out The Percentage Increase

Take a look at our How to Work Out Percentage Increase/Decrease page.

This page is all about finding the percentage increase or decrease between two numbers.

We also have a percentage increase calculator that will work it all out for you at the click of a button.

• How to Work out the Percentage Increase or Decrease

Don’t Miss: Exponential Growth And Decay Common Core Algebra 1 Homework Answers

It May Seem Intimidating To Learn Mathematical Terminology In A It Is Useful To Be Able To Talk About Percentages In English Because You Might Use Figures Fractions And Percentages In Your Work In A Course Or Even

How to find the percent of something is often a matter of keeping your starting and ending points straight.

You May Download Best Here: CONVERT FRACTIONS INTO PERCENTS

4 Ways to Do Percentages on a Calculator – wikiHow

Find The Percentage Of A Given Number – YouTube

Calculate Percentages on your Finger Tips – YouTube

How do you Calculate Percentages? – A Plus Topper

How Do You Find Out a Percent of a Number? | Sciencing

Maths help: What is a percentage? How do you work out a …

How do you Calculate Percentages? – A Plus Topper

Finding Percentages without a Calculator – Mr-Mathematics.com

How do you convert a fraction to a percentage? Learn how in this simple tutorial. Textbooks differ and I have been.

How To Calculate The Average Percentage

Follow the steps to calculate the average percentage: The average percentage can be calculated by dividing the total items represented in percentages by the overall total of items. In other words,

Calculate the average percentage by dividing the total items represented by percentages by the overall total of items

• Convert the percentage into decimal numbers. For example, to calculate the average of 30% of 50 and 20% of 80, we convert them into their decimal forms that are 0.3 and 0.2 respectively.
• Write the number represented by each decimal number. In this case, it will be;0.3×50=15;and;0.2×80=16;respectively.
• Add the numbers thus obtained. .
• Find the sum of sample sizes. .
• Divide the total number obtained in Step 3 by the number obtained in Step 4. So,;31/130=0.24. This decimal number represents 24% which is the required average percenatge.

Also Check: Exponential Growth And Decay Common Core Algebra 1 Homework Answers

How To Calculate Percentages

There are many online calculators to find percentages, but percentages can be calculated manually by following these steps:

Common Error When Finding A Percentage

Since percentages are often thought of as parts of a larger whole thing, there can be a tendency to divide instead of multiply when faced with a problem such as find 35% of 80. As the example below shows, after converting the percent to a decimal, the next step is to multiply, not divide.

An understanding of percent allows students to estimate to check whether their answer is reasonable. In this example, knowing that 35% is between one-quarter and one-half would mean the answer should be somewhere between 20 and 40.

You May Like: Geometry Segment Addition Postulate Worksheet

Examples Of Percentage Calculations

The following two examples show how to calculate percentages.

1) 12 people out of a total of 25 were female. What percentage were female?

2) The price of a $1.50 candy bar is increased by 20%. What was the new price?

3) The tax on an item is $6.00. The tax rate is 15%. What is the price without tax?

Similar types of problems to those in the examples above are solved in a series of three mini-lessons on;Calculating with Percent. These are listed below.

6% of 31 is 1.86

You can practice calculating percentages by first finding 1% and then multiplying to get your final answer using;this Calculating Percentages in Two Steps Worksheet.;There are also;more percentage worksheets here too.

Reverse Percentage Calculator 2

This calculator will help you to find the original number, when you have been given the final number and the percentage increase or decrease.

Example: if a toy in a sale marked 20% off costs $210, what is the original price.

Simply enter the final number in the first box and the percentage in the 2nd box and whether it was increased or decreased.

Answers are rounded to 2dp.

Don’t Miss: Write The Segment Addition Postulate For The Points Described

What Is The Percentage

Percentage is one of many ways to express a dimensionless ratio of two numbers. It’s very popular since it can describe situations that involve large numbers , average as well as very small ones .

One percent is a hundredth. As a percent sign, we usually use %, but sometimes it is denoted by pct. It means that 5 percent is the same as 5%, 5 pct, 0.05, 5/100, or five-hundredths. It is as simple as that, and this percentage calculator is a tool dedicated to working with decimal fractions and percentages. If you’re seeking more complicated problems, try to figure out how to calculate the percentage of a percentage.

This is all nice, but we usually do not use percents just by themselves. Mostly, we want to answer how big is one number in relation to another number?. To try to visualize it, imagine that we have something everyone likes, for example, a large packet of cookies . Let’s try to find an answer to the question of what is 40% of 20? It is 40 hundredths of 20, so if we divided 20 cookies into 100 even parts , 40 of those parts would be 40% of 20 cookies. Let’s do the math: 40/100 * 20 = 8. A handy little tip: to divide by 100, simply move the dot two spaces to the left. In our calculation, 40/100 * 20 could be done as /100 . 40 * 20 is 800. By moving the dot in 800 by two digits to the left, you get 8.00, and when you get rid of all unnecessary zeros, you obtain 8. In our calculator, enter 40 and 20 .