Boolean Algebras: The Definition
The Boolean algebras we have seen so far have all been concrete, consisting of bit vectors or equivalently of subsets of some set. Such a Boolean algebra consists of a set and operations on that set which can be shown to satisfy the laws of Boolean algebra.
Instead of showing that the Boolean laws are satisfied, we can instead postulate a set X, two binary operations on X, and one unary operation, and require that those operations satisfy the laws of Boolean algebra. The elements of X need not be bit vectors or subsets but can be anything at all. This leads to the more general abstract definition.
- A Boolean algebra is any set with binary operations and and a unary operation ¬ thereon satisfying the Boolean laws.
For the purposes of this definition it is irrelevant how the operations came to satisfy the laws, whether by fiat or proof. All concrete Boolean algebras satisfy the laws , whence every concrete Boolean algebra is a Boolean algebra according to our definitions. This axiomatic definition of a Boolean algebra as a set and certain operations satisfying certain laws or axioms is entirely analogous to the abstract definitions of group, ring, field etc. characteristic of modern or abstract algebra.
- A Boolean algebra is a complemented distributive lattice.
The section on axiomatization lists other axiomatizations, any of which can be made the basis of an equivalent definition.
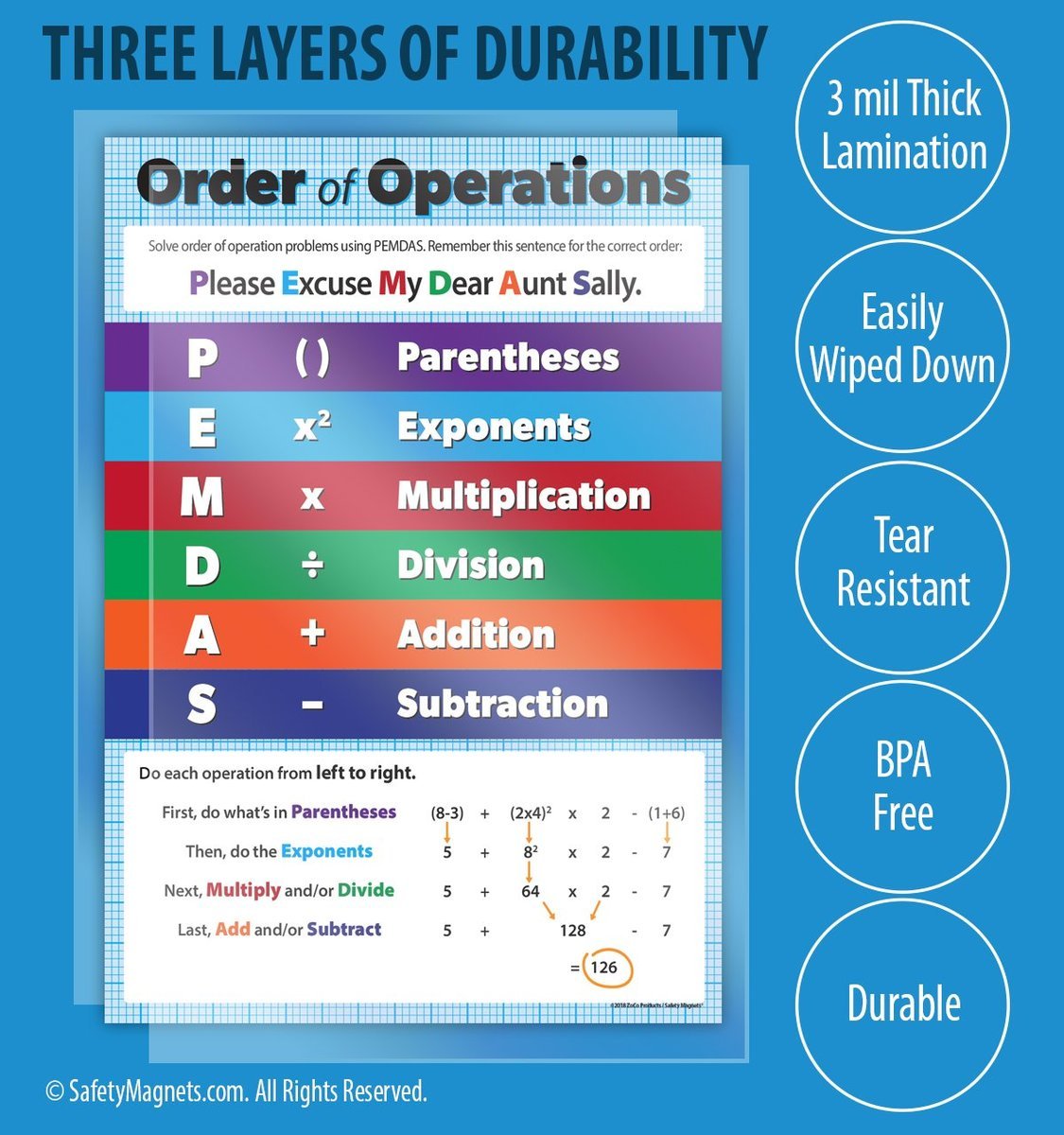
Operations In The Correct Order
When you are faced with a mathematical expression that has several operations or parentheses, the solution may be affected by the order in which you tackle the operations. For example, take the expression
$$4\cdot 7-2$$
If we do the multiplication first, we arrive at the following answer:
$$28-2=26$$
If instead we begin by substracting, we get:
$$4\cdot 5= 20$$
In order to avoid confusion and to ensure that everyone always arrives at the same result, mathematicians established a standard order of operations for calculations that involve more than one arithmetic operation. Arithmetic operations should always be carried out in the following order:
Example
Suppose you want to figure out how many hours a person works in two days assuming that they work 4 hours before lunch and 3 hours after lunch each day. First, work out how many hours the person works each day:
$$4+3=7$$
and then multiply that by the number of days the person worked:
$$7\cdot 2=14$$
If we were to write this example as one expression, we would need to use parentheses to make sure that people calculate the addition first:
$$\left \cdot 2=14$$
Deductive Systems For Propositional Logic
An axiomatization of propositional calculus is a set of tautologies called axioms and one or more inference rules for producing new tautologies from old. A proof in an axiom system A is a finite nonempty sequence of propositions each of which is either an instance of an axiom of A or follows by some rule of A from propositions appearing earlier in the proof . The last proposition is the theorem proved by the proof. Every nonempty initial segment of a proof is itself a proof, whence every proposition in a proof is itself a theorem. An axiomatization is sound when every theorem is a tautology, and complete when every tautology is a theorem.
Entailment differs from implication in that whereas the latter is a binary operation that returns a value in a Boolean algebra, the former is a binary relation which either holds or does not hold. In this sense entailment is an external form of implication, meaning external to the Boolean algebra, thinking of the reader of the sequent as also being external and interpreting and comparing antecedents and succedents in some Boolean algebra. The natural interpretation of is as in the partial order of the Boolean algebra defined by x y just when xy = y. This ability to mix external implication and internal implication in the one logic is among the essential differences between sequent calculus and propositional calculus.
Don’t Miss: Abiotic Features Definition
Formal Definition Of A Group
A group is a set G, combined with an operation *, such that:
Let’s look at those one at a time:
1. The group contains an identity. If we use the operation on any element and the identity, we will get that element back.
For the integers and addition, the identity is “0”. Because 5+0 = 5 and 0+5 = 5
In other words it leaves other elements unchanged when combined with them.
There is only one identity element for every group
The symbol for the identity element is e, or sometimes 0. But you need to start seeing 0 as a symbol rather than a number. 0 is just the symbol for the identity, just in the same way e is. It’s defined that way. In fact, many times mathematicians prefer to use 0 rather than e because it is much more natural.
| Formal Statement:There exists an e in the set G, such that a * e = a and e * a = a, for all elements a in G |
2. The group contains inverses. If we have an element of the group, there’s another element of the group such that when we use the operator on both of them, we get e, the identity.
For the integers and addition, the inverse of 5 is -5.
In just the same way, for negative integers, the inverses are positives. -5 + 5 = 0, so the inverse of -5 is 5. In fact, if a is the inverse of b, then it must be that b is the inverse of a.
Inverses are unique. You can’t name any other number x, such that 5 + x = 0 besides -5.
a * = * c
Read more about closure.
The Prototypical Boolean Algebra
The set and its Boolean operations as treated above can be understood as the special case of bit vectors of length one, which by the identification of bit vectors with subsets can also be understood as the two subsets of a one-element set. We call this the prototypical Boolean algebra, justified by the following observation.
- The laws satisfied by all nondegenerate concrete Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.
This observation is easily proved as follows. Certainly any law satisfied by all concrete Boolean algebras is satisfied by the prototypical one since it is concrete. Conversely any law that fails for some concrete Boolean algebra must have failed at a particular bit position, in which case that position by itself furnishes a one-bit counterexample to that law. Nondegeneracy ensures the existence of at least one bit position because there is only one empty bit vector.
The final goal of the next section can be understood as eliminating “concrete” from the above observation. We shall however reach that goal via the surprisingly stronger observation that, up to isomorphism, all Boolean algebras are concrete.
Recommended Reading: Michael Jacksons Biological Kids
Special Types Of Groups: Abelian
Before I go on to talk about Abelian, let me point out that it is pronounced a-be-lian. Not abe-lian. I made that mistake when I was first reading about groups, and I still have yet to break the habit.
If a * e = a, doesn’t that mean that e * a = a?
And similarly, if a * b = e, doesn’t that mean that b * a = e?
Well, as a matter of fact, it does. But we are careful here because in general, it is not true thata * b = b * a. But when it is true that a * b = b * a for all a and b in the group, then we call that group an abelian group.
That fact is true for integers, and this is why we call the integers with addition an abelian group.
Inverse Operation Of Classic Diffraction Integral
In laser applications research, the inverse diffraction operation is a very important step. For example, the wavefront reconstruction of the object light field in digital holography and the design of binary optical elements involve the inverse diffraction operation. However, in view of the Fresnel diffraction strictly satisfying the wave equation in several classic diffraction integral paraxial approximations, discussing the classic diffraction integral inversion has important implications.
Because the light propagation is a diffraction-limited propagation process, even if in free space, only the angular spectrum component met by 1 > 0 can reach the observation screen . Therefore, it is impossible to obtain the wave field on the diffractive plane according to the wave field on the observation plane. However, in practice, it is of great significance that the angular spectrum component of the diffractive plane can be solved by wave field on the observation plane.
4.6.1Kirchhoff Transfer Function Method
According to Eq. , we can obtain
4.6.2RayleighSommerfeld Transfer Function Method
According to Eq. , we can obtain
4.6.3Angular Spectrum Transfer Function Method
According to Eq. , we can obtain
Jon Rokne, in, 1992
Interval arithmetic has some drawbacks as well:
Robert L. Page, in, 2003
Don’t Miss: Which Founding Contributors To Psychology Helped Develop Behaviorism
How Do You Find B In Slope Intercept Form
Steps to find the equation of a line from two points:
Example: Integers And Addition
Consider the integers. Can you name the identity element of integers when it comes to addition? We want to find a + e = e + a = a. OK, you know already. 0 is the identity. That is because a + 0 = 0 + a = a, for any integer a.
Sticking with the integers, let’s say we have a number a. Can we find it’s inverse? That is, does there exist an a1such that a + a1 = a1 + a = e? For example, 5 + 51 = 0? What is 51? -5 is the answer. To a + -a = e, for the integers.
If I add two integers together, will the result be an integer? Yes. So it is closed.
Finally, does a + = + c? It does! And guess what, we just showed that the integers are a group with respect to addition.
Recommended Reading: Why Are There Different Branches Of Chemistry
Introduction To The Order Of Operations
How would you solve this problem?
12 – 2 5 + 1
The answer you get will depend largely on the order in which you solve the problem. For example, if you work the problem from left to right12-2, then 105, then add 1you’ll get 51.
12 – 2 5 + 150 + 151
On the other hand, if you solve the problem in the opposite directionfrom right to leftthe answer will be 0.
12 – 2 5 + 112 – 120
Finally, what if you did the math in a slightly different order? If you multiply first, then add, the answer is 3.
12 – 2 5 + 12 + 13
It turns out that 3 actually is the correct answer because it’s the answer you get when you follow the standard order of operations. The order of operations is a rule that tells you the right order in which to solve different parts of a math problem.
The order of operations is important because it guarantees that people can all read and solve a problem in the same way. Without a standard order of operations, formulas for real-world calculations in finance and science would be pretty uselessand it would be difficult to know if you were getting the right answer on a math test!
Summary Of Algebraic Structures
- Professor at University of California, Davis
Loosely speaking, an algebraic structure is any set upon which “arithmetic-like” operations have been defined. The importance of such structures in abstract mathematics cannot be overstated. By recognized a given set \ as an instance of a well-known algebraic structure, every result that is known about that abstract algebraic structure is then automatically also known to hold for \. This utility is, in large part, the main motivation behind abstraction.
Before reviewing the algebraic structures that are most important to the study of Linear Algebra, we first carefully define what it means for an operation to be “arithmetic-like”.
Read Also: What Is Figure Ground Perception Psychology
Relational Algebra What Is Relational Algebra
Relation Algebra is a procedural query language for RDBMS . An Algebra based on the set of operators and operand. Edgar F. Codd created it for a relational database. Relational Algebra provides a fundamental query for retrieving data from databases. The retrieved result from algebra expression is a relation which formed from one or more relations. Relational Algebra specifies many operations to manipulate relations.
Procedural Query Language is language in which user tells the system to perform a specific operation to obtain the desired result.
SQL Query language used by users in these days based on the concept of relational algebra and relational Calculus. In these days, most Commercial RDBMSs are not providing us the platform or user interface for using Relational algebra query language. Relational algebra considered as an integral part of the relational query. SQL query is parsed into Relational algebra expression through parser than into executable code.
Algebra provides us a great range of operations to perform on relations. Relational Algebra function can divide into two parts, Basic set operations, and Special Relational Operations. Relational algebra used operand, operators, rules in algebraic expressions.
Basic set operations: Union, Intersection, Difference and Cartesian product.
Special Set Operations: Join, Selection, Projection, and Division
Lets us discuss all the operation one by one
Syntax:
Let us consider a table Employee, having four columns.
| Eid |
What Is Join Operation In Relational Algebra

OPERATION IN RELATIONAL ALGEBRAJoinJOINJOIN operation
. Simply so, what is the role of JOIN operation in relational algebra?
Join Operations: A Join operation combines related tuples from different relations, if and only if a given join condition is satisfied. It is denoted by .
One may also ask, what is join operation? A join is an SQL operation performed to establish a connection between two or more database tables based on matching columns, thereby creating a relationship between the tables. There are different types of joins.
Also question is, what are the relational algebra operations?
Relational Algebra. Relational algebra is a procedural query language, which takes instances of relations as input and yields instances of relations as output. It uses operators to perform queries. An operator can be either unary or binary. They accept relations as their input and yield relations as their output.
What is Cartesian product operation in relational algebra?
The Cartesian Product is also an operator which works on two sets. It is sometimes called the CROSS PRODUCT or CROSS JOIN. It combines the tuples of one relation with all the tuples of the other relation.
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Using The Order Of Operations
The standard order of operations is:
In other words, in any math problem you must start by calculating the parentheses first, then the exponents, then multiplication and division, then addition and subtraction. For operations on the same level, solve from left to right. For instance, if your problem contains more than one exponent, you’d solve the leftmost one first, then work right.
Let’s look at the order of operations more closely and try another problem. This one might look complicated, but it’s mainly simple arithmetic. You can solve it using the order of operations and some skills you already have.
4 / 2 3 + + 18 / 32 – 8
Parentheses
Always start with operations contained within parentheses. Parentheses are used to group parts of an expression.
If there is more than one set of parentheses, first solve for the ones on the left. In this problem, we only have one set:
4 / 2 3 + + 18 / 32 – 8
In any parentheses, you follow the order of operations just like you do with any other part of a math problem.
Here, we have two operations: addition and multiplication. Because multiplication always comes first, we’ll start by multiplying 6 2 .
4 / 2 3 + + 18 / 32 – 8
62 is 12. Next, we’ll add4.
4 / 2 3 + + 18 / 32 – 8
4+12 is 16. So we’ve simplified our parentheses to 16. Since we just have a single number in the parentheses, we can get rid of them all togetherthey’re not grouping together anything now.
C2 Groups Fields And Vector Spaces
We begin this section with the following definition, which is unequivocably one of the most fundamental and ubiquitous notions in all of abstract mathematics.
Definition C.2.1.
Let \ be a nonempty set, and let \ be a binary operation on \. is a function with \\) denoted by \, for each \.) Then \ is said to form a group under \ if the following three conditions are satisfied:
You should recognize these three conditions as properties that are satisfied by the operation of addition on \. This is not an accident. In particular, given real numbers \, the group axioms form the minimal set of assumptions needed in order to solve the equation \ for the variable \, and it is in this sense that the group axioms are an abstraction of the most fundamental properties of addition of real numbers.
A similar remark holds regarding multiplication on \ and solving the equation \ for the variable \. Note, however, that this cannot be extended to all of \.
Because the group axioms are so general, they are particularly useful in building more complicated algebraic structures. This is done by adding any number of additional axioms, the most fundamental of which is as follows.
Definition C.2.2. Let \ be a group under binary operation \. Then \ is called an abelian group if, given any two elements \, \.
Example C.2.3.
Recommended Reading: Geometry Segment Addition Postulate Worksheet