Make Muffins Using A Proportional Relationship
To make 1 dozen muffins, you need 2 eggs. If you want to make 2 dozen muffins, you need 4 eggs. To make 3 dozen muffins, you need 6 eggs. 1 times 2 is 2, 2 times 2 is 4, 3 times 2 is 6. The number of eggs is always 2 times the number of batches of muffins. This is called a proportional relationship. Now you try: How can you tell if the following data represents a proportional relationship? 1:3, 2:6, 3:9, 4:12
What Is The Difference Between Direct And Inverse Proportion
The difference between direct and inverse proportion is that the direct proportion shows a direct relationship between the two quantities where an increase in one also leads to an increase in the other quantity and vice-versa. On the other hand, inverse proportion represents an indirect relation between two quantities or variables where an increase in one leads to a decrease in the other variable, and vice-versa.
What Is Proportional On A Graph
Non-Proportional: How to tell the difference: A proportional graph is a straight line that always goes through the origin. A non-proportional graph is a straight line that does not go through the origin.
What is meant by proportional in physics?
In physics, we often talk about proportionality. This is a relationship between two quantities where they increase or decrease at the same rate. In other words, when quantity A changes by a certain factor, quantity B will change by the same factor.
You May Like: Multiple View Geometry In Computer Vision Book
How Do You Know If Two Variables Are Directly Proportional
If one variable is always the product of the other variable and a constant, the two are said to be directly proportional. x and y are directly proportional if the ratio yx is constant.
What is an intuitive explanation of the concept of directly proportional?
Concept in mathematics. The variable y is directly proportional to the variable x with proportionality constant ~0.6. The variable y is inversely proportional to the variable x with proportionality constant 1.
What Is Inverse Proportion
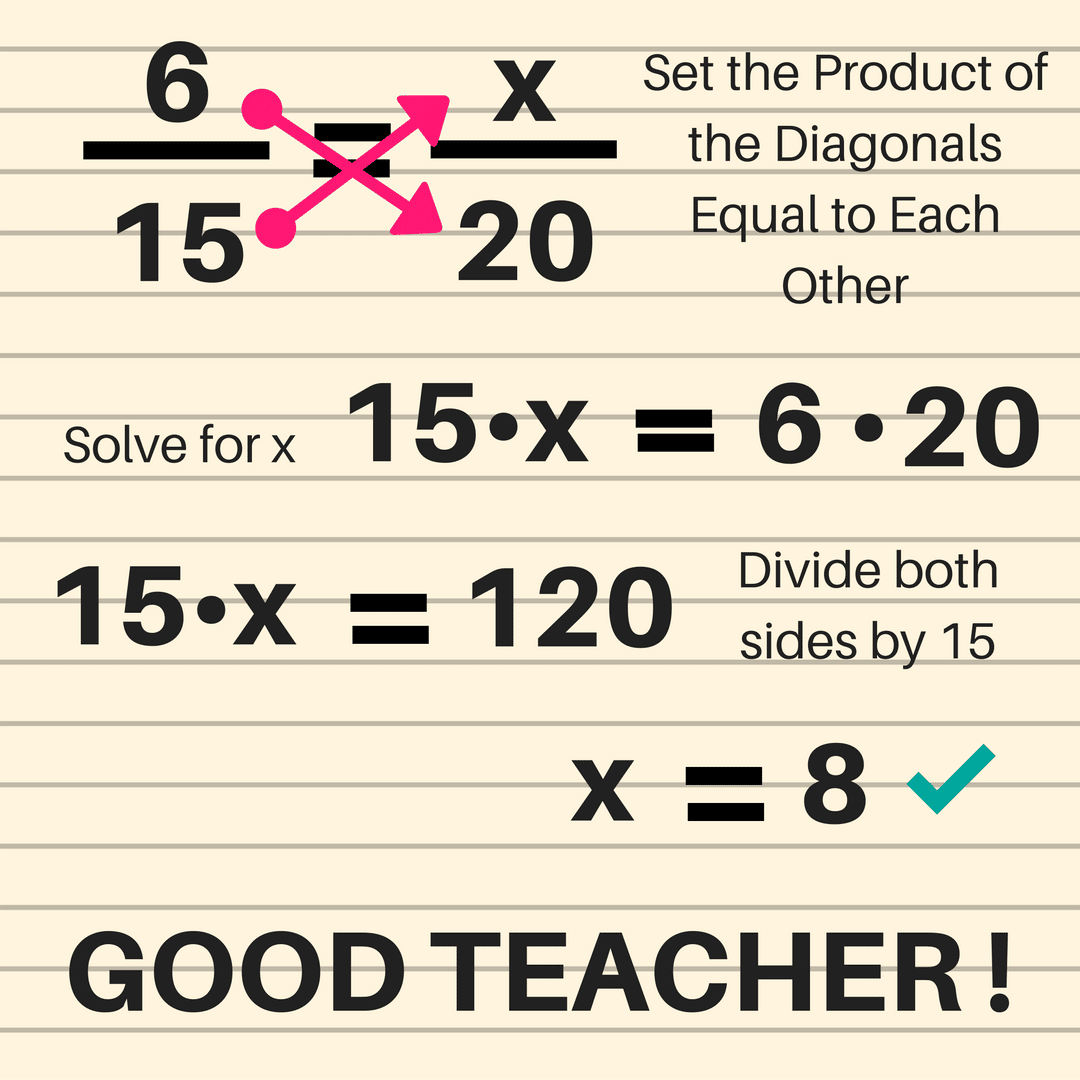
The definition of inverse proportion states that “Two quantities are said to be in inverse proportion if an increase in one leads to a decrease in the other quantity and a decrease in one leads to an increase in the other quantity”. In other words, if the product of both the quantities, irrespective of a change in their values, is equal to a constant value, then they are said to be in inverse proportion. For example, let us take the number of workers and the number of days required by them to complete a given amount of work as x and y respectively.
| Numbers of Workers | Number of Days Required |
|---|---|
| 16 | |
| 4 | 12 |
Are the number of workers and the number of days in inverse proportional relation? Let’s find out.
Observe the values written in the table carefully. You will find out that for each row, the product of x and y are the same. That means if there are 16 workers, they will complete the work in 3 days. So, here x × y = 16 × 3 = 48. Now, we decrease the number of workers, it is obvious that the less number of workers will do the same work in more time. But we see the product of x and y here, it is 12 × 4 = 48. Again, for 8 workers in 6 days, the product is 48. And same for 4 workers in 12 days. So, the product of two quantities in inverse proportion is always equal.
Recommended Reading: What Does Diffraction Mean In Physics
What Is The Difference Between Proportionally And Proportionately
Proportionally vs Proportionately Whats the difference? is that proportionally is in proportion in due degree adapted relatively while proportionately is in a proportionate manner with due proportion proportionally. Other Comparisons: Whats the difference?
What is the difference between direct and inverse proportionality?
The concept of inverse proportionality can be contrasted with direct proportionality. Consider two variables said to be inversely proportional to each other. If all other variables are held constant, the magnitude or absolute value of one inversely proportional variable decreases if the other variable increases,
You Can Recognize Proportional Relationships In Equations And Graphs
Equations that represent proportional relationships are always in the form y=kx, where k is the constant of proportionality. That means that the relationship between x and y is always multiplicative, with nothing added or subtracted. Unlike y=2x, y=2x+4 and y=2x-5 do not represent proportional relationships. 4 is added or 5 is subtracted from the product. The graph of a proportional relationship is always a straight line that passes through the origin, . Now you try: Identify which equation represent proportional relationships: a) y=7.7x b) y=3x+5 c) y=13x
Recommended Reading: What Is B In Math
What Does Being Proportional Mean
Question:
Two concurrent forces act along the sides CA and CB of a triangle. Their magnitudes are proportional to $\cos $ and $\cos $ respectively. Prove that their resultant is proportional to $\sin$.
My book’s attempt:
Let the forces acting along $CA$ and $CB$ be $\vec$ and $\vec$ respectively. Let the resultant of $\vec$ and $\vec$ be $\vec$, which is acting along $CD$. Now, let $P=k\cos$, $Q=k\cos$, where $k$ is the constant of proportionality.
$$….$$
$$$$
My comments:
If $P$ is proportional to $\cos$, it means that $P=n\cos$. Again, if $Q$ is proportional to $\cos$, it means that $Q=s\cos$. Furthermore, if $R$ is proportional to $\sin$, it means that $R=t\sin$. Now, the constants of proportionality $n,s,t$ needn’t be equal. Why did my book assume that the constants were equal i.e. why did my book assume:
$$n=s=t=k$$
My question:
- 2$\begingroup$When it says CA and CB are proportional means that $\frac=\frac =\frac$ where as it says k is constant of proportionality.$\endgroup$
Question:
Two concurrent forces act along the sides CA and CB of a triangle.Their magnitudes are proportional to $\cos $ and $\cos $respectively.
My book’s attempt:
Let the forces acting along $CA$ and $CB$ be $\vec$ and $\vec$respectively. Let the resultant of $\vec$ and $\vec$ be$\vec.$
What Does Proportionally Mean In Math
proportionality, In algebra, equality between two ratios. The term proportionality describes any relationship that is always in the same ratio. The number of apples in a crop, for example, is proportional to the number of trees in the orchard, the ratio of proportionality being the average number of apples per tree.
What means proportionality?
noun. the fact or quality of being in proper balance or relation as to size or quantity, degree, severity, etc.:Even a defensive response to an unjust attack may go far beyond legitimate defense if it causes destruction that violates the principle of proportionality.
Don’t Miss: What Is The Purpose Of Psychology
What Is Proportion In Math
Proportion is a mathematical comparison between two numbers. According to proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other. Proportions are denoted using the symbol :: or =. For example, 2:5 :: 4:8 or 2/5 = 4/8. Here, 2 and 8 are the extremes, while 5 and 4 are the means.
What Are Direct Proportions
If two variables are in direct proportion, as one variable increases, then so does the other. Conversely, it means as one variable decreases, then so does the other. Any direct relationship, for variables A and B, can be written as A = kB. This means on a graph, this relationship will be represented as a straight line, passing through the origin. This is shown below.
Graph showing a direct relationship of the form A = kB
The weight of a piece of string is directly proportional to its length. When the piece of string is 30cm long, it weighs 0.2N. Find the weight of the piece of string when the string is 50 cm long. We know that this is directly proportional, so we know the relationship WL, when W represents weight, and L represents length. Let a be our constant of proportionality, so that W = aL. From the first part of the question, we know , so . We can now use this to find the weight when the string is 50cm long. The same relation holds, so . Substituting in our length of 50 cm, we get , so to two decimal places, W = 0.33N.
Recommended Reading: Algebra 1 Chapter 2 Practice 2 3 Answers
How To Solve The Constant Of Proportionality
We apply our knowledge on the direct and inverse variations, identify them and then determine the constant of proportionality and thereby get the solutions to our problems.
Example 1:Find the constant of proportionality, if y=24 and x=3 and y x.
Solution: We know that y varies proportionally with x. We can write the equation of the proportional relationship as y = kx. Substitute the given x and y values, and solve for k.
24 = k
Important notes
- To check if the 2 quantities are proportional or not, we have to find the ratio of the two quantities for all the given values. If their ratios are equal, then they exhibit a proportional relationship. If all the ratios are not equal, then the relation between them is not proportional.
- If two quantities are proportional to one another, the relationship between them can be defined by y = kx, where k is the constant ratio of y-values to corresponding x-values.
- The same relationship can also be defined by the formula x=y, where 1/k is now the constant ratio of x-values to y-values.
Why Do We Use The Constant Of Proportionality

We use constant of proportionality in mathematics to calculate the rate of change and at the same time determine if it is direct variation or inverse variation that we are dealing with. Let us assume that the cost of 2 apples = $20. We determine that the cost of 1 apple = $10. We have found the Constant of Proportionality for the cost of an apple is 2.
If we want to draw a picture of the Taj Mahal by sitting in front of it on a piece of paper by looking at the real image in front of us, we should maintain a proportional relationship between the measures of length, height, and width of the building. We need to identify the constant of proportionality to get the desired outcome. Based on this, we can draw the monument with proportional measurements. For instance, if the height of the dome is 2 meters then in our drawing we can represent the same dome with height 2 inches. Similarly, we can draw other parts. In such scenarios, we use constant of proportionality.
Working with proportional relationships allows one to solve many real-life problems such as:
You May Like: Where Can I Take Algebra 2 Over The Summer
What Symbol Do We Use For Proportion
To represent that two variables are proportional to one another, we use the symbol . For example, Ohm’s law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Letting voltage be represented by V, and current by I, then we can write .
Whenever we see a proportionality symbol, we can replace this with an equals sign and a proportionality constant. This means we could write Ohm’s law as V = kI, where k is our constant.
What Are Inverse Proportions
Inverse proportion occurs when one variable increasing causes another variable to decrease. If this relationship were to occur between the variables c and d, we would write c . An example of an inverse proportion would be as speed increases, then the time to travel a distance will decrease. Graphically, this means that the shape of the relationship will be represented by y = k / x, with k constant, and x, y variables. This means that the graph will never touch the axis, but it will get very very close as we put a very big x value in, or an x value extremely close to 0. This is shown below.
Graph showing an inversely proportional relationship
Two variables, b and n are inversely proportional to one another. When b = 6, n = 2. Find the value of n when b is 15. We know b , so , when k is our constant of proportionality. Filling in values of b and n, we get , so k = 12. This means for all values of b and n, b = 12 / n. We need to find n when b = 15, so we can fill this in, to get 15 = 12 / n. Rearranging this for n, we get n = 12/15 = 0.8.
You May Like: Is The Geometry Eoc Hard
What Is Direct Proportion And Inverse Proportion
Direct proportion, as the name suggests, indicates that an increase in one quantity will also increase the value of the other quantity and a decrease in one quantity will also decrease the value of the other quantity. While inverse proportion shows an inverse relationship between the two given quantities. It means an increase in one will decrease the value of the other quantity and vice-versa.
What Is The Opposite Of Proportionate
Opposite of corresponding in size or amount to something else. disproportionate. nonproportionate. unproportionate. dissimilar.
What is another term for a proportional relationship?
In this page you can discover 25 synonyms, antonyms, idiomatic expressions, and related words for proportional, like: equal, comparable, comparative, correlative, equivalent, big, commensurate, corresponding, even, reciprocal and relative.
Read Also: What Is Delta In Geography
What Are Different Types Of Proportion
Based on the type of relationship two or more quantities share, the proportion can be classified into different types. There are two types of proportions.
- Direct Proportion- describes the direct relationship between two quantities. In simple words, if one quantity increases, the other quantity also increases and vice-versa.
- Inverse Proportion- describes the indirect relationship between two quantities. In simple words, if one quantity increases, the other quantity decreases and vice-versa.
You Can Describe Proportional Relationships Using Equations
Every kitten has 2 ears. You can write an equation to show how the number of kittens is related to the number of ears. Let x be the number of kittens and y be the number of ears. So, y=2x, since the number of ears is always twice the number of kittens. You can plug in any number of kittens for x to find the number of ears, y. For example, 5 kittens have y = 2 × 5 = 10 ears. Now you try: Write an equation to describe the relationship between the number of dogs and the number of legs in all.
Read Also: What Are Ethical Principles In Psychology
How Do You Use The Word Proportional
Proportional in a Sentence
What does the term proportional refer to?
Proportion says that two ratios are equal. Example: 1/3 = 2/6.
What are some statements of proportionality?
A proportionality statement for the function will be that the function is proportional to the cube of x and inversely proportional to the square of p. F c = m v t 2 r where v_t is the tangential velocity and r is the radius.
What is an example of proportional relationship?
Proportions are the same ratios written in different forms. A proportional relationship is states that they are the same. For example, 1/2 and 6/12 have a proportional relationship, which means they are the same. I hope this helps!!
What does proportionately mean?
Definition of proportionately in English: proportionately. adverb. In a way that corresponds in size or amount to something else. the risk of harm increases proportionately with the dose. a small rise in price will cause a proportionately smaller drop in sales.
What Is Constant Of Proportionality

Constant of proportionality is the constant value of the ratio between two proportional quantities. Two varying quantities are said to be in a relation of proportionality when, either their ratio or their product yields a constant. The value of the constant of proportionality depends on the type of proportion between the two given quantities: Direct Variation and Inverse Variation.
- Direct Variation: The equation for direct proportionality is y = kx, which shows as x increases, y also increases at the same rate. Example: The cost per item is directly proportional to the number of items purchased, expressed as y x
- Inverse Variation: The equation for the indirect proportionality is y = k/x, which shows that as y increases, x decreases and vice-versa. Example:The speed of a moving vehicle inversely varies as the time taken to cover a certain distance, expressed as y 1/x
In both the cases, k is constant. The value of this constant is called the coefficient of proportionality. The constant of proportionality is also known as unit rate.
You May Like: What Does Concentration Mean In Chemistry
Direct Proportion Vs Inverse Proportion
There are two types of proportionality that can be established based on the relation between the two given quantities. Those are direct proportion and inverse proportional. Two quantities are directly proportional to each other when an increase or decrease in one leads to an increase or decrease in the other. While on the other hand, two quantities are said to be in inverse proportion if an increase in one quantity leads to a decrease in the other, and vice-versa. The graph of direct proportion is a straight line while the inverse proportion graph is a curve. Look at the image given below to understand the difference between direct proportion and inverse proportion.