What Does Difference Mean In Calculus
In calculus , differentiate a function means to take a derivative of a function. Lets say you have a variable y which is a function of variable x i.e y=f When I do differentiation , it helps to check how much y changes when I change x with an infinitesimal amount i.e to check dy with respect to dx.
What Is The Apostrophe Is Geometry Called
A transformation in Geometry is much like a translation in Algebra. When we talk about transformations, we call the original shape the preimage. After the shape has moved, we call it the image. The image of a point is written with the same letter, followed by an apostrophe. In math, an apostrophe is read as prime.
What Is The Meaning Of Difference In This Question
I was given the following problem:
Let $X$ represent the difference between the number of heads and the number of tails obtained when a coin is tossed $n$ times. What are the possible values of $X$?
which already has an answer on this site. However, when I first approached this, I interpreted the word “difference” as the distance between two points lying on a horizontal/vertical line, and therefore always positive . Similar questions on the lexical use of the word in math, agree that the definition of difference is given by Big number – small number. On the other hand, Wikipedia states that difference is the result of subtraction, and therefore may be negative. At this point, I guess this is left to the interpretation of the reader, since to me the question is ambiguously phrased.
Not content, I wanted to see if there existed any probability distributions with discrete support on $\mathbb$. I found out on the Wikipedia list that only $2$ are mentioned, namely the Degenerate distribution and Rademacher distribution. Every other distribution mentioned is defined on $\mathbb$. So my question is, knowing this and what was mentioned in the paragraph above, wouldn’t the best answer only include positive values of $X$? As most problems of this type involve Binomial distributions, Geometric distributions, etc. which are defined on $\mathbb$.
Read Also: What Is The Molecular Geometry Of Ccl4
Other Differences Between British And American English
In some cases, British and American English use different words for the same concept. For example, American English speakers use the words truck, shopping cart, and sweater British English speakers say lorry, trolley, and jumper to mean the same things.
In other cases, the differences between British and American English words are much more subtle. For instance, American English uses the term racecar, while British English uses the word racing car.
In still other cases, British and American English words differ by just one letter, as in the case of math and maths. British English includes U in the spelling of French-derived words, such as colour or favourite, which American English omits.
This also happens with the words sport and sports. In American English, youd say, I enjoy playing sports, and I also like watching sports. In British English, this sentence would be I enjoy playing sport, and I also like watching sport. This time, its American English that likes the s!
How Do You Calculate Mean Vs Average
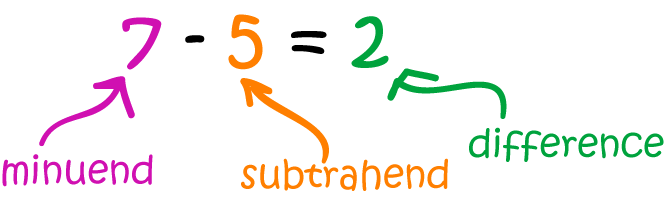
The mean is the average of the numbers and to calculate both averages and mean we need to add up all the values, then divide by the total number of values. In other words, it is the sum of the values divided by the count of the values. The formulas for both are more or less the same. Average = Mean = Sum/Count
Read Also: Geometry Basics Segment Addition Postulate Answer Key
Q14 What Is The Meaning Of Twice In Math
Answer: 2x, where x is any number.
Double or multiply any number with two in simple words.
For instance, twice of four is eight.
Twice of 2.5 is five., Twice of 5Y is 10Y.
Similarly, thrice means three times or multiplying any number with three. Like thrice of 20 = 60, thrice of three = nine, and thrice of 40X = 120X.
The Teaching Of Subtraction In Schools
Methods used to teach subtraction to elementary school vary from country to country, and within a country, different methods are adopted at different times. In what is known in the United States as traditional mathematics, a specific process is taught to students at the end of the 1st year for use with multi-digit whole numbers, and is extended in either the fourth or fifth grade to include of fractional numbers.
Also Check: Holt Geometry Lesson 4.5 Practice B Answers
What Is The Difference Between Average And Mean
Average and mean are usually confused with one another as both the mathematical terms are used to explain the set of numbers. Mean can simply be calculated by adding the set of values and divided by the number of quantities. Thus, this is the core definition of what mean is. You can find the tabular column below to learn the difference between the average and mean.
| Difference between Average and Mean | |
|---|---|
|
Average |
Mean |
| Average can simply be defined as the sum of all the numbers divided by the total number of values. | A mean is defined as the mathematical average of the set of two or more data values. |
| Average is usually defined as mean or arithmetic mean. | Mean is simply a method of describing the average of the sample. |
| Average can be calculated for any discrete numbers where it assumes uniform distribution. | It is mainly used in Statistics, and it is applied for any distribution such as geometric, binomial, Poisson distribution, and so on. |
| The arithmetic mean is considered as a form of average. | There are various types of mean. |
| Average is usually used in conversations in general day to day English. | Mean is used in a more technical and mathematical sense. |
| The average is capable of giving us the median and the mode. | Mean, on the other hand, cannot give us the median or mode. |
How Do You Interpret Mean Difference
For example, lets say the mean score on a depression test for a group of 100 middle-aged men is 35 and for 100 middle-aged women it is 25. If you took a large number of samples from both these groups and calculated the mean differences, the mean of all of the differences between all sample means would be 35 25 = 10.
You May Like: Does Elton John Have Kids
Math Symbols In Real Life
You use math symbols more than you realize in all areas of your life. As noted above, the difference between a plus or minus symbol in banking can indicate whether you’re adding a wealth of funds to your bank account or in withdrawing funds. If you’ve ever used a computer accounting spreadsheet, you likely know that the big sum sign gives you an easyindeed instantway to add an endless column of numbers.
“Pi,” which is denoted by the Greek letter , is used throughout the world of math, science, physics, architecture, and more. Despite the origins of pi in the subject of geometry, this number has applications throughout mathematics and even shows up in the subjects of statistics and probability. And the symbol for infinity not only is an important math concept, but it also suggests the infinite expanse of the universe or the infinite possibilities that come from every action or thought .
How Do I Find The Difference Between Two Numbers
Percentage Change | Increase and Decrease
You May Like: Why Are There Different Branches Of Chemistry
How To Use Math And Maths
The only difference between math and maths is where theyre used. Math is the preferred term in the United States and Canada. Maths is the preferred term in the United Kingdom, Ireland, Australia, and other English-speaking places.
Theres no real logical explanation as to why math became preferred in some places while maths was elsewhere. The usual argument goes that mathematics is plural because it ends in an -s, so maths should be its abbreviation. The problem is that, while it ends in an s, mathematics is a mass noun and usually takes a singular verb .
Both of these words date back to the turn of the 20th century. There are examples of math in writings from the 1840s, and of maths from the 1910s.
What Does Doing Math Mean
Since I study neither gender issues nor genetics,and since I am not a scientist , the only”authority” I can bring to the question is inthe area of mathematical ability, so that’s whatI’ll stick to here.
As it happens, the question is fairly closelyrelated to the topic of that new book that’s got meonto the media circuit in the first place, namelythe innate mathematical abilities of various livingcreatures, including – but not exclusively – humans.
The first thing to observe is that the very question”Are men on average better than women at math?” isnot sufficiently precise. Expressed that way, thequestion implicitly assumes that mathematicalability is a single mental capacity. It’s not.
“Doing math” involves all kinds of mentalcapacities: numerical reasoning, quantitativereasoning, linguistic reasoning, symbolic reasoning,spatial reasoning, logical reasoning, diagrammaticreasoning, reasoning about causality, the abilityto handle abstractions, and maybe some others Ihave overlooked. And for success, all those need tobe topped off with a dose of raw creativityand a desire – for some of us an inner need – topursue the subject and do well at it.
But that is not what I want to discuss today. I wantto go back to that question of what it meansto do mathematics. That might seem to be a prettysimple question, but unless you take a particularlydogmatic stance on the matter, it turns out to beextraordinarily difficult to come up with an answer.
Also Check: Geometry Lesson 1.7 Answers
What Does And Mean In Math
Mathematics is a wonderful subject and has its vocabulary and uses many English words like AND, OR, Equal to, Union, and nor, to name a few.
AND & OR are the two most confusing aspects for many students because they dont understand whether they mean addition or multiplication.
The problem increases when we study these keywords in the probability chapter, where both these become critical.
We must understand one thing that these both are operations and not simply the signs like multiplying or dividing.
What Does AND Mean in Math?
In probability, the distinction is clear, and in simple math logic symbol, + means AND.
- AND needs both conditions to be true to be valid true means satisfying the conditions.
- OR is mostly okay with anyone or both the conditions getting true for it takes place.
What Does The Word Each Mean In Math
eachperaverage
Of is a powerful word in mathematics, for it can mean a fraction of something, e.g. 4/5 of 25 which commands multiplication or which can imply quotients in some cases such as probability.
Beside above, what does total add or subtract mean math? Adding two numbers means to find their sum . Subtracting one number from another number is to find the difference between them. Multiplication means times . A product is the result of the multiplication of two numbers. Division ‘undoes’ multiplication.
Besides, what words tell you to multiply?
The Basic Operations
Recommended Reading: Law Of Figure And Ground
Comparing The Two Main Methods
Both these methods break up the subtraction as a process of one digit subtractions by place value. Starting with a least significant digit, a subtraction of the subtrahend:
- sjsjâ1 … s1
from the minuend
- mkmkâ1 … m1,
where each si and mi is a digit, proceeds by writing down m1 â s1, m2 â s2, and so forth, as long as si does not exceed mi. Otherwise, mi is increased by 10 and some other digit is modified to correct for this increase. The American method corrects by attempting to decrease the minuend digit mi+1 by one . The European method corrects by increasing the subtrahend digit si+1 by one.
Example: 704 â 512.
c e & \color -1\\& C& D& U\\& 7& 0& 4\\& 5& 1& 2\\\hline & 1& 9& 2\\\end}\longleftarrow }}\\\\\longleftarrow \ }\\\longleftarrow \ }\\\longleftarrow }\\\end}}
The Austrian method does not reduce the 7 to 6. Rather it increases the subtrahend hundred’s digit by one. A small mark is made near or below this digit . Then the subtraction proceeds by asking what number when increased by 1, and 5 is added to it, makes 7. The answer is 1, and is written down in the result’s hundred’s place.
The Differential Doesnt Have To Be At The End
One consequence of teaching students that the differential in an integral means only with respect to x can be seen in the following question, from 2003, about a relatively unusual variation in the notation:
Integral Notation - Missing IntegrandsI have seen some integral notation used that I am not familiar with. It looks like this: / | dx f + .../There does not seem to be an integrand . I'm not sure if f is to be integrated. I have two theories, but I can't see the point in writing the expression as it is if either of my theories is correct.My theories about what this might mean:1) The above notation is the same as writing: / | 1 dx f + ... /= * f + ... 2) The rest of the expression is to be integrated with respect to x.If is correct, then what was the point of writing the integral - why wasn't just written instead? If is correct, then how does one know when to "stop integrating" .I have seen this recently in multi-variate calculus, i.e. when x is in R^n rather than R: does this situation justify the use of the integral notation somehow?
Chriss first guess is that the dx closes off the integral, so that what follows is to be multiplied the second is that it doesnt matter where the dx is placed.
I answered:
In writing this, it has occurred to me that my reference to commutativity is not quite valid, specifically when it comes to definite integrals. The following are not the same: $$\int_0^b\int_0^a fdx dy\ne\int_0^b\int_0^a fdy dx$$
Chris replied,
Read Also: Does Elton John Have Biological Children
How Do You Write Thompsons
Lack of attention to this distinction is the cause of frequent errors in signage, as when a sign referring to the inhabitants of a residence reads, The Thompsons. This truncation of the Thompsons house literally indicates that it is the house of the Thompson and therefore is incorrect it should read, The
Understanding The And & Or Probabilities:
- For instance, what is the probability of if we take out a card from its deck and it must be red AND face card?
- As per the meaning of the term AND, we need to look at the joint probability of such a card which satisfies both conditions of the outcome from this sample.
- There are only six possible cards here which Jack, Queen, and a King of Hearts and diamonds.
- Using formula, P = 6/52 = 11.5% approx.
- Now, what if the same question asked to take out a card that has Red OR a face card?
- Now, the meaning has changed completely.
- We can pick any card, whether its red, a face card, or both red and a face.
- This gives us twenty-six cards in total, which are red, which already include the face card in themselves, and six cards as both.
- We now have thirty-two such cards, which give us P = 32/ 52 deck has fifty-two cards in total, = 61.5% approx.
- See how changing just one word AND to OR changed the answer by so much.
PS In the OR problem, we do not add twelve face cards to twenty-six red cards because we already have six face cards that are red as well.
If one is not careful, he will get 38 cards instead of 32.
You May Like: How Do Noise Cancelling Headphones Work Physics
What Does A Mini Circle Between F And H Mean
I am currently doing a math problem and have come across an unfamiliar notation.A mini circle between $f$ and $h$
The question ask me to find for ‘the functions $f=2x-1$ and $h=3x+2$’
$$f \circ h$$
However, I can’t do this as I do not know what the circle notation denotes to.Does it mean to multiply?
This notation means that you take the output of $h$ and use it as the input of $f$. When we are working with a specific $x$ value, we can suggestively write $f)$ instead.
For instance if $f=1/z$ and $h=2+3x$ then $$ = f\big\big) = f = \frac.$$
The circle $\circ$ is the symbol for composition of functions. In General, if you have two functions $g\colon X\rightarrow Y$ and $f\colon Y\rightarrow Z$, then$f\circ g$ is a function from $X$ to $Z$. For $x\in X$ one has $ = f)$.
In your case one has: $f = 2x-1$, $g = 3x+2$ and $$ = f) = 2)-1 = 2 -1 = 6x+3.$$You take the function $g$ and put it in place of the $x$ in the function $f$.
This is obviously different from $f\cdot g = \cdot = 6x^2+x-2$.
Definition Of Average And Mean

Average: The term Average describes a value that should represent the sample. An average is defined as the sum of all the values divided by the total number of values in a given set. It is also known as the arithmetic mean. Let us consider a simple data to find the average.
Given, the set of values are 1, 2, 3, 4, 5.
Average = Sum of all the values/ Total number of values
Average = /5 = 15/5 = 3
Mean: A mean is a mathematical term, that describes the average of a sample. In Statistics, the definition of the mean is similar to the average.
Also Check: How To Find Average Speed In Physics