The Square Root Function
In this section we turn our attention to the square root function, the function defined by the equation
We begin the section by drawing the graph of the function, then we address the domain and range. After that, well investigate a number of different transformations of the function.
Inverses And Radical Functions
In this section, you will:
- Find the inverse of an invertible polynomial function.
- Restrict the domain to find the inverse of a polynomial function.
Park rangers and other trail managers may construct rock piles, stacks, or other arrangements, usually called cairns, to mark trails or other landmarks. A cairn in the form of a mound of gravel is in the shape of a cone with the height equal to twice the radius.
The volume is found using a formula from elementary geometry.
We have written the volume V in terms of the radius r r . However, in some cases, we may start out with the volume and want to find the radius. For example: A customer purchases 100 cubic feet of gravel to construct a cone shape mound with a height twice the radius. What are the radius and height of the new cone? To answer this question, we use the formula
This function is the inverse of the formula for V r .
In this section, we will explore the inverses of polynomial and rational functions and in particular the radical functions we encounter in the process.
Restricting The Domain To Find The Inverse Of A Polynomial Function
So far, we have been able to find the inverse functions of cubic functions without having to restrict their domains. However, as we know, not all cubic polynomials are one-to-one. Some functions that are not one-to-one may have their domain restricted so that they are one-to-one, but only over that domain. The function over the restricted domain would then have an inverse function. Since quadratic functions are not one-to-one, we must restrict their domain in order to find their inverses.
Also Check: Prentice Hall Geometry Slader
The Graph Of The Square Root Function
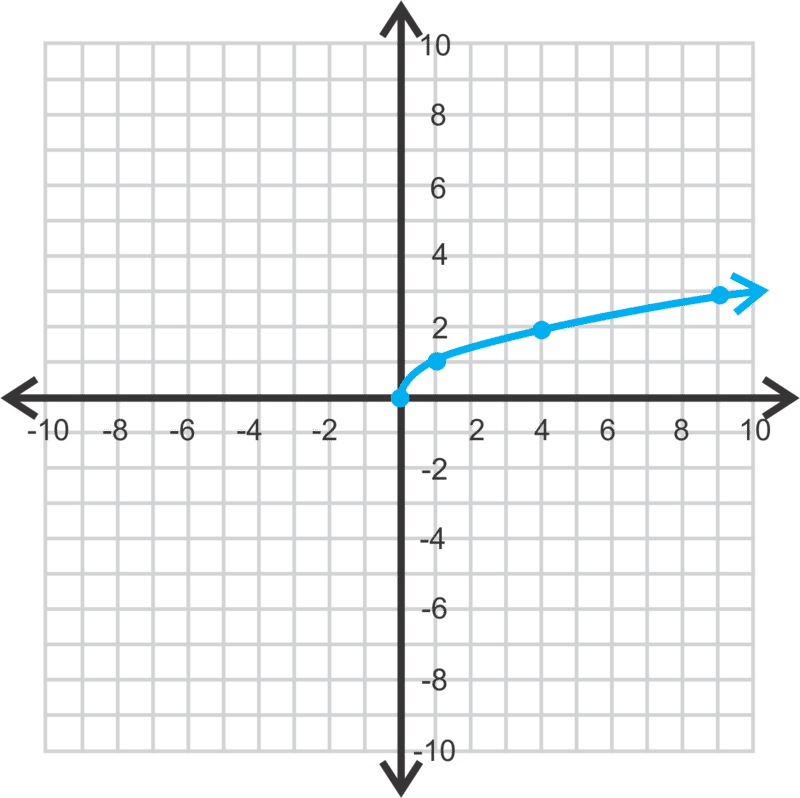
Lets create a table of points that satisfy the equation of the function, then plot the points from the table on a Cartesian coordinate system on graph paper. Well continue creating and plotting points until we are convinced of the eventual shape of the graph.
We know we cannot take the square root of a negative number. Therefore, we dont want to put any negative x-values in our table. To further simplify our computations, lets use numbers whose square root is easily calculated. This brings to mind perfect squares such as 0, 1, 4, 9, and so on. Weve placed these numbers as x-values in the table in Figure 1, then calculated the square root of each. In Figure 1, you see each of the points from the table plotted as a solid dot. If we continue to add points to the table, plot them, the graph will eventually fill in and take the shape of the solid curve shown in Figure 1.
The point plotting approach used to draw the graph of \ = \sqrt\) in Figure 1 is a tested and familiar procedure. However, a more sophisticated approach involves the theory of inverses developed in the previous chapter.
To find the equation of the inverse, recall that the procedure requires that we switch the roles of x and y, then solve the resulting equation for y. Thus, first write \ = x^2\), \, in the form
Next, switch x and y.
When we solve this last equation for y, we get two solutions,
The sequence of graphs in Figure 2 also help us identify the domain and range of the square root function.
Graphing Square Root Functions
The parent function of the functions of the form f
Note that the of f
can be obtained by translating the graph of f units to the right and then b
Step 1: Draw the graph of y
Step 2: Move the graph of y unit to the right to obtain the graph of y
Step 3: Move the graph of y units up to obtain the graph of y
The domain of the function y
The range of the function y
You May Like: Renate Blauel 2013
The Graph Of A Radical Function
A radical as you might remember is something that is under a radical sign e.g. a square root. A radical function contains a radical expression with the independent variable in the radicand. Usually radical equations where the radical is a square root is called square root functions.
An example of a radical function would be
$$y=\sqrt$$
This is the parent square root function and its graph looks like
If we compare this to the square root function
$$y=a\sqrt$$
We will notice that the graph stretches or shrinks vertically when we vary a
$$\begin \left | a \right | > 0\: \: \: \: \: \: \: & & \Rightarrow vertical\: stretch \\ 0< \left | a \right |< 1 & & \Rightarrow vertical\: shrink\: \: \: \\ \end$$
In the graph below we have radical functions with different values of a
If a < 0 the graph
$$y=a\sqrt$$
Is the reflection in the x-axis of the graph
$$y=\left |a \right |\sqrt$$
Another square root equation would be
$$y=a\sqrt+c$$
If you look at the graphs above which all have c = 0 you can see that they all have a range 0 . If you have a c 0 you’ll have a radical function that starts in . An example of this can be seen in the graph below
The value of b tells us where the domain of the radical function begins. Again if you look at the parent function it has a b = 0 and thus begin in If you have a b 0 then the radical function starts in .
If both b 0 and c 0 then the radical function starts in
Finding The Inverse Of A Polynomial Function
Two functions are inverse functions if for every coordinate pair in f there exists a corresponding coordinate pair in the inverse function, g ) . In other words, the coordinate pairs of the inverse functions have the input and output interchanged. Only one-to-one functions have inverses. Recall that a one-to-one function has a unique output value for each input value and passes the horizontal line test.
For example, suppose the Sustainability Club builds a water runoff collector in the shape of a parabolic trough as shown in Figure 2. We can use the information in the figure to find the surface area of the water in the trough as a function of the depth of the water.
Because it will be helpful to have an equation for the parabolic cross-sectional shape, we will impose a coordinate system at the cross section, with x measured vertically, with the origin at the vertex of the parabola. See Figure 3.
From this we find an equation for the parabolic shape. We placed the origin at the vertex of the parabola, so we know the equation will have form y 2 . Our equation will need to pass through the point , from which we can solve for the stretch factor a
Our parabolic cross section has the equation
To find an inverse, we can restrict our original function to a limited domain on which it is one-to-one. In this case, it makes sense to restrict ourselves to positive x values. On this domain, we can find an inverse by solving for the input variable:
Also Check: Definition Of Similar In Geometry
How To
Given a polynomial function, find the inverse of the function by restricting the domain in such a way that the new function is one-to-one.
Finding the Inverse of a Cubic Function
Find the inverse of the function f 1.
Solution
This is a transformation of the basic cubic toolkit function, and based on our knowledge of that function, we know it is one-to-one. Solving for the inverse by solving for x
Look at the graph of f Notice that one graph is the reflection of the other about the line y This is always the case when graphing a function and its inverse function.
Also, since the method involved interchanging x is on the graph of f is on the graph of f is on the graph of f is on the graph of f is on the graph of f is on the graph of f
Find the inverse function of f .