What Is Intersection In Math

How Do You Find The Basis Of Intersection

Direct link to this answer

Should I Learn Excel Or Sql First

Although both Excel and SQL dwell in tables and columns, they serve very different needs. So no, theres no correlation in learning Excel first and then SQL. Here you can hone your REGEX skills so you can make your queries more intelligent since you can ditch a lot of WHEREs in favor of a single REGEX.

How Do You Find The Point Of Intersection With Two Equations

To find the point of intersection algebraically, solve each equation for y, set the two expressions for y equal to each other, solve for x, and plug the value of x into either of the original equations to find the corresponding y-value. The values of x and y are the x- and y-values of the point of intersection.

Read Also: How To Find Half Life Chemistry

Notation For Set Intersection

Set intersection is an important concept in set theory. Therefore, it deserves a proper notation. The symbol is used to indicate the intersection between sets. This symbol indicates the intersection between any two sets, say A and B.

Consider any two sets, A and B. Their intersection is given as:

A B

The concept of intersection is not restricted to only two sets. It can extend to a group of sets. Consider a group of sets containing the sets A, B, C, and D. The intersection between these sets is given as:

A B C D

Lets solve an example related to the intersection of sets.

Example 4

The intersection of these three sets is given as:

A B C

It can be evaluated as,

A B C =

A B C =

This represents the intersection between the three sets A, B, and C.

Intersection Of Two Sets Representation

If X and Y are two sets, then the intersection of two sets is represented by

X Y = n + n – n

Where n is the cardinal number of set X, n is the cardinal number of set Y, n is the cardinal number of union of set X and Y.

To understand the concept of intersection of two sets clearly, let us consider an example.

If Set X = , Set Y = and Set Z = . Find the Intersection of

1. Set X and Y

2. Set Y and Z

3. Set A and C

Solution:

• Intersection of set X and Y is X Y

Set of all the elements which are common to both set X and Y is

• Intersection of set Y and Z is Y Z

Set of all the elements which are common to both set Y and Z is

• Intersection of set X and Z is X Z

Set of all the elements which are common to both set X and Z is

Don’t Miss: Prentice Hall Gold Geometry Answer Key

Intersection With The Universal Set

For the other extreme, what happens when we examine the intersection of a set with the universal set? Similar to how the word universe is used in astronomy to mean everything, the universal set contains every element. It follows that every element of our set is also an element of the universal set. Thus the intersection of any set with the universal set is the set that we started with.

Again our notation comes to the rescue to express this identity more succinctly. For any set A and the universal set U, A U=A.

What Is Intersection Of Sets

In set theory, for any two sets A and B, the intersection is defined as the set of all the elements in set A that are also present in set B. We use the symbol ” that denotes ‘intersection of’. For example, let us represent the students who like ice creams for dessert, Brandon, Sophie, Luke, and Jess. This is set A. The students who like brownies for dessert are Ron, Sophie, Mia, and Luke. This is set B. The students who like both ice creams and brownies are Sophie and Luke. This is represented as A B.

Don’t Miss: Is Elton John The Biological Father Of Elijah

What Is The Intersection Of Two Events In Probability

The chance of all of two or more events occurring is called the intersection of events. For independent events, the probability of the intersection of two or more events is the product of the probabilities. In the case of two coin flips, for example, the probability of observing two heads is 1/2*1/2 = 1/4.

Representation Of Intersection Using Venn Diagram

As we have highlighted time and again how important Venn diagrams are for visualizing sets and the different operations we can perform on them.

So, lets give a quick background on Venn diagrams. Venn diagram is the most appropriate tool to understand the operations on sets in a comprehensive manner. They are used to represent finite sets only. All the region covered under a curve is represented as one set. Whereas the elements of that particular set are represented using points inside the region of the diagram.

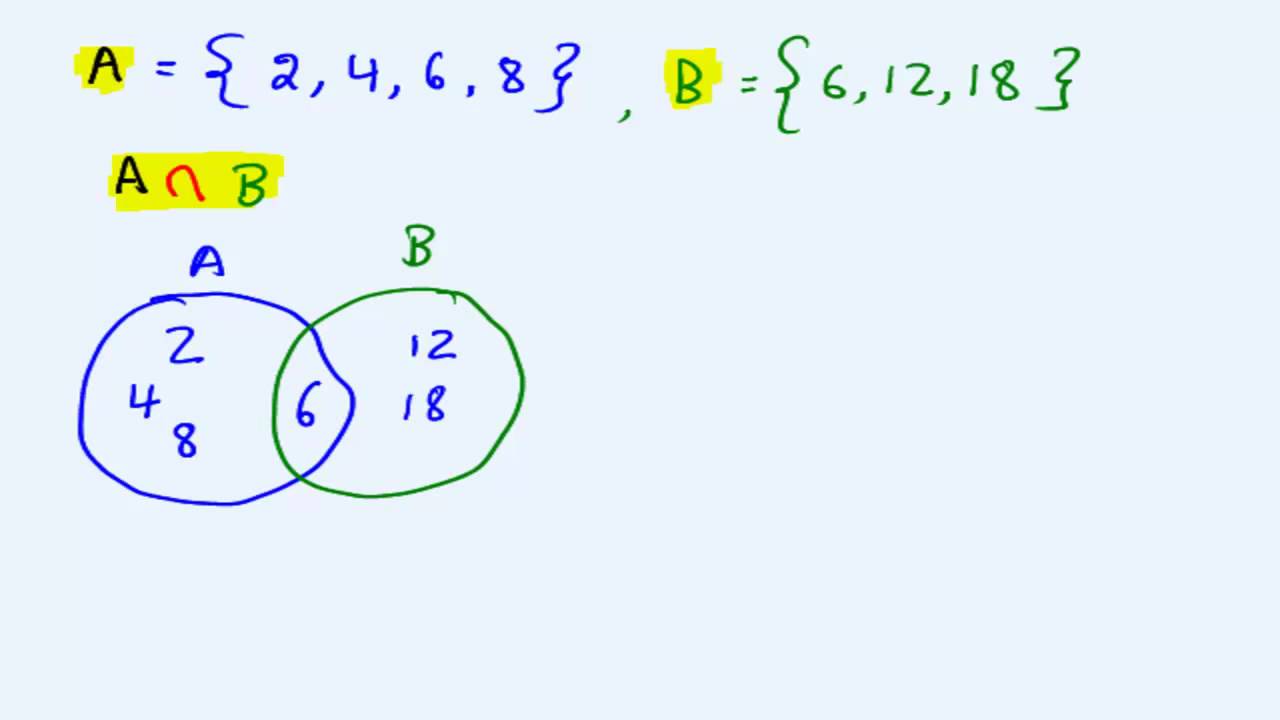
Let us say, U represents a universal set, sets A and B are subsets of this universal set. For example, if A = and B = , then their intersection is as follows:

A B =

A and e are the only two common elements between sets A and B.

To represent them with a Venn diagram, we will use two circles, one for set A and one for set B. the universal set U, in this case, is the set of alphabets to which both sets A and B would belong to. Following is the Venn diagram representation of the intersection:

The shaded blue area represents the intersection between A and B.

Here, we show only two sets, a Venn Diagram of any operation can be constructed using multiple sets, as long as they are finite.

Lets solve some examples to learn how to construct our very own Venn diagram.

Example 3

Consider a set A = and set B = . Show the intersection between A and B through Venn diagram. Let set U = .

Solution:

The intersection between the two sets A and B can be determined as:

And,

You May Like: How Do We Know That Clocks Are Hungry

Intersection Of Three Sets

It is possible to find the intersection of more than two sets. In this section, you will learn how to find the intersection of three sets. Suppose A, B and C are three sets, then the intersection of these three sets is the set of all elements that are common to A, B and C. This can be represented as A B C. This can be better understood with the help of the example given below.

For example, A = , B = and C = .

The intersection of these 3 sets can be expressed as, A B C.

Let us identify the common elements of the given sets.

12 is the only common element in A, B and C.

Therefore, A B C =

What Type Of System If It Has No Solution

A system has no solution if the equations are inconsistent, they are contradictory. for example 2x+3y=10, 2x+3y=12 has no solution. is the rref form of the matrix for this system. The row of 0s only means that one of the original equations was redundant. The solution set would be exactly the same if it were removed.

Recommended Reading: Geometry Dash Hack Tool

Intersecting And Disjoint Sets

We say that that is an element of both A in which case we also say that A is an inhabited set, meaning that there exists some x

We say that In plain language, they have no elements in common. A are disjoint if their intersection is empty, denoted A

For example, the sets } } are disjoint, while the set of even numbers intersects the set of multiples of 3 at the multiples of 6.

Binary intersection is an associative operation that is, for any sets A

Intersection distributes over union and union distributes over intersection. That is, for any sets A

The most general notion is the intersection of an arbitrary nonempty collection of sets.If M is a nonempty set whose elements are themselves sets, then x is an element of the intersection of M if and only if for every element A

The notation for this last concept can vary considerably. Set theorists will sometimes write ” “, while others will instead write ” A} “.The latter notation can be generalized to ” A_} “, which refers to the intersection of the collection :i\in I\right\}.} Here is a nonempty set, and A is a set for every i

In the case that the index set I is the set of natural numbers, notation analogous to that of an infinite product may be seen:

The Union And Intersection Of Two Sets

All statistics classes include questions about probabilities involving the union and intersections of sets. In English, we use the words “Or”, and “And” to describe these concepts. For example, “Find the probability that a student is taking a mathematics class or a science class.” That is expressing the union of the two sets in words. “What is the probability that a nurse has a bachelor’s degree and more than five years of experience working in a hospital.” That is expressing the intersection of two sets. In this section we will learn how to decipher these types of sentences and will learn about the meaning of unions and intersections.

Don’t Miss: Geometry Dash Verify Hack

What Is The Intersection Of Sets

Now that we have covered the set union lets move onto the second topic about the intersection of sets.

The intersection of sets is used to indicate the common elements shared by two or more sets. In other words, we can say that the set that represents the intersection of sets includes the elements that belong to any set A but are also a part of any set B. So, we can conclude that the intersection of sets indicates the common elements between the sets.

The concept of intersection is not only restricted to two sets. We can also extend it to three, four, or more sets.

To understand the intersection of sets, consider the following example.

Example 3

Find the intersection of these two sets.

Solution

The intersection indicates the common elements shared by the two sets. Upon analyzing, the common element shared by these two sets is only one, and that element is 6. So the intersection of sets A and B is .

The Notation For Intersection Of Sets

Delving further into the intersection of sets, our next step is to talk about the notation used to represent sets intersection. The intersection between any two sets, A and B, is represented by the symbol . Like the symbol used for the union of sets, this symbol is used between the operands. The operands, in this case, are the names denoting the sets.

This method of notation is called the infix notation. In this notation, the operator is surrounded by the operands. The operator, in our case, is . It is, most commonly, used to refer to binary operations. We know that intersection, as the union of sets, is also a binary operation.

An example of this would be as follows:

Then the intersection of these sets is denoted by:

A B

So, whenever we want to express the intersection between two sets, this is how we do it symbolically. It is an expression of set A intersecting set B.

Lets solve some examples to understand the intersection of sets.

Example 2

If sets A and B are defined as:

Find out the intersection of set A and B.

Solution:

The intersection of two sets is defined as the set containing elements in set A which are also present in set B in other words, the common elements.

As we can see, 12, 14, 1, 9 are the elements present in both set A and set B. So, we have the intersection of sets equal to:

A B =

You May Like: Geometry Dash Hack No Survey

Intersection Of Sets Using Venn Diagram

The intersection of two sets can be represented using the Venn diagram as shown below.

In the above diagram, the shaded portion represents the intersection of two sets A and B.

Similarly, we can draw a Venn diagram for the intersection of 3 sets as shown below.

In the above diagram, we can see that the centermost region denotes the intersection of three sets A, B and C.

Union And Intersection Of Sets

The union of two sets P and Q is represented by P Q. This is the set of all different elements that are included in P or Q. The symbol used to represent the union of set is .

The intersection of two set P and Q is represented by P Q. This is the set of all different elements that are included in both P and Q. The symbol used to represent the intersection of set is . We can say that the intersection of two given sets i.e. P and Q is the set that includes all the elements that are common to both P and Q.

If P = and Q =

What are P Q, and P Q

Solution:

P Q =

P Q =

A great way of learning Union And Intersection of Sets is by using Venn diagrams. The venn diagram of union and intersection is discussed below.

You May Like: What Is The Value Of The Bond Angles In Ccl4

What Does The Intersection Of Two Or More Events Mean

Intersection refers to the outcomes that are in both event A and event B at the same time. Explain the difference between the union and the intersection of two or more events. Union means one event or the other event must be represented. Intersection means both events are represented at the same time.

What Is The Difference Between An Union And An Intersection

Main Differences Between Union and Intersection Mathematically, a union of two sets is a set consisting of all the values from both the sets removing the duplicate values. A union is represented by U and intersection is represented by . A union discards duplicates values. The number of elements of a union is greater than or equal to parent sets. In practice, a union is the addition of sets.

Don’t Miss: Bridge To Algebra Answers

Difference Between Union And Intersection Of Set

Intersection With The Empty Set

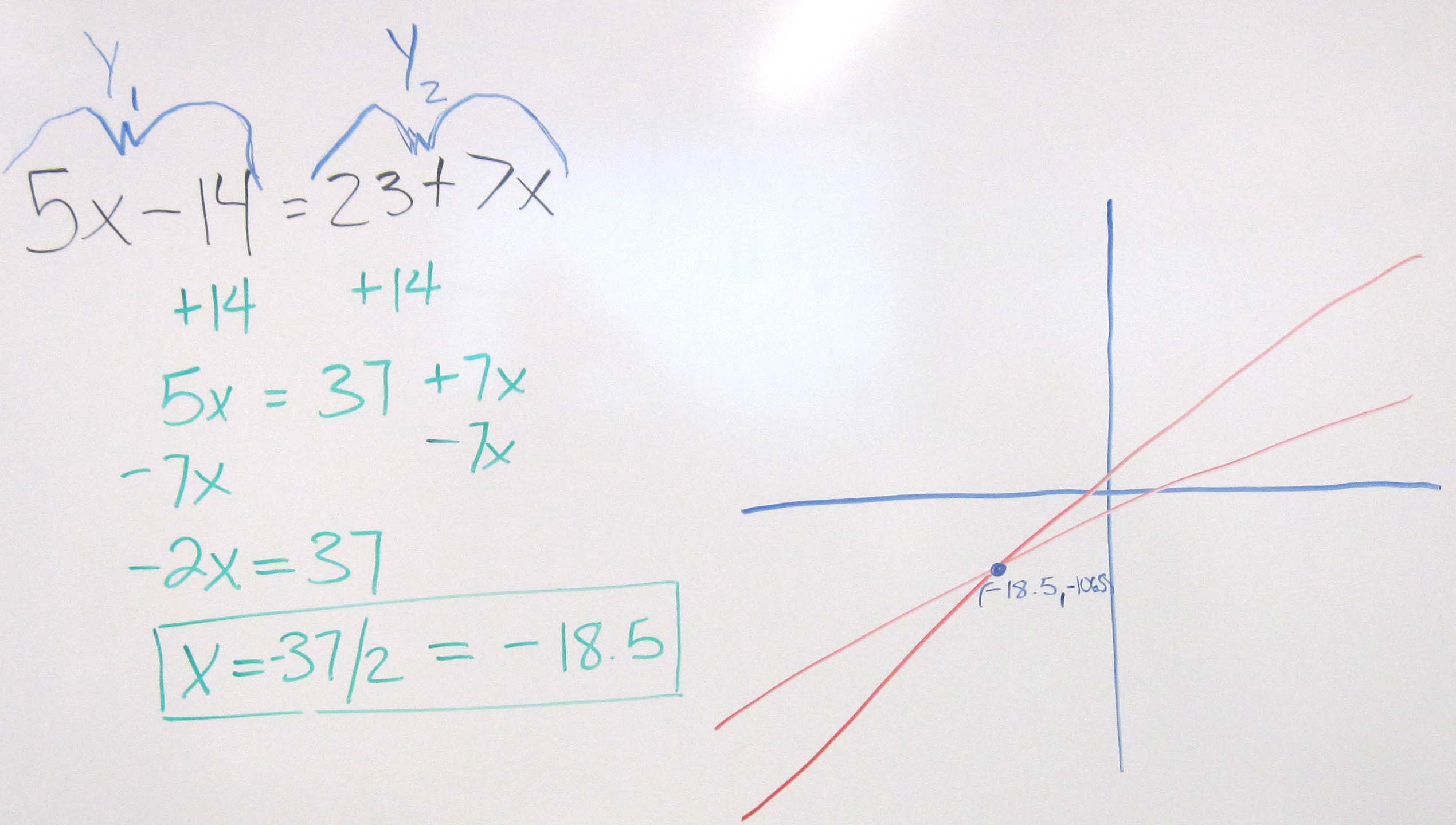
One basic identity that involves the intersection shows us what happens when we take the intersection of any set with the empty set, denoted by #8709. The empty set is the set with no elements. If there are no elements in at least one of the sets we are trying to find the intersection of, then the two sets have no elements in common. In other words, the intersection of any set with the empty set will give us the empty set.

This identity becomes even more compact with the use of our notation. We have the identity: A = .

You May Like: Holt Mcdougal Geometry Worksheet Answers

Functions: Graphs And Intersections

are two functions that take a real number input, and output a real number.

Then the intersection points of f

Sometimes the exact values can be easily found by solving the equation f

What are the points of intersection of the functions f

Now, you can use the value of x -coordinate of the point of intersection.

Substitute the value of in any of the two functions.

g = 3

The equations can also be solved graphically by plotting the two functions on a coordinate plane and identifying the point of intersection of the two.

In other cases, the exact values can be hard to find. You may need to use technology to estimate them.

Example 2:

Find the point of intersection of the two functions.

Here, solving algebraically is not so easy .The solutions to the equation | are not nice-looking rational numbers.

Graph the functions on a .

You can use a graphing utility to find that the coordinates of the intersection points are approximately ( .