Video Transcript : Free Fall In Translational Motion
Leah here from leah4ci.com/MCAT and in this video well talk about Free Fall as itll show up on your MCAT in a Kinematics question.
Free fall as the name implies is when something falls under its own acceleration, meaning you dont have an outside force that causes it to accelerate in any direction other than straight down. When dealing with Free Fall, we use the standard Kinematic equations.
But realize that anytime X shows up, you want to use Y and anytime Accelerations shows up, you want to use the acceleration of gravity or simply g for gravity. Gravitys 9.8m/s2 but on the MCAT you can simplify and well use 10 meters per second squared with the negative to imply that the direction is downward.
The three equations to consider for Free Fall have acceleration in them. The first is V final is equal to V initial plus at . We wanna swap out the a for g and since gravity is down, we change gt plus to minus because negative implies a negative or downward direction.
The second one is V final squared is equal to V initial squared plus two a delta X. We wanna swap the X for a Y, a for g and then put a negative for the direction of gravity. And finally the last one is delta x is equal to V intial t plus one over two a t squared. We switch the x to a y , we put negative and swap the a for a g.
Well look at this in a more detail when we talk about Projectile Motion but now lets try a simple free fall problem. In this problem, were told that:
What Factors Affect The Motion Of A Projectile Launched Horizontally
Initial velocity, the initial height the projectile is being launched from, and gravity will all affect a projectile launched horizontally. Air resistance will also have an effect in real life, but for most theoretical calculations it is negligible and is therefore ignored. If the projectile has wings, this will also impact its motion, as it will glide.
Icle Trajectories In Cylindrical
It is often convenient to formulate the trajectory of a particle r = , y, z) using polar coordinates in the XâY plane. In this case, its velocity and acceleration take a convenient form.
Recall that the trajectory of a particle P is defined by its coordinate vector r measured in a fixed reference frame F. As the particle moves, its coordinate vector r traces its trajectory, which is a curve in space, given by:
ijkXYZF
Consider a particle P that moves only on the surface of a circular cylinder r = constant, it is possible to align the Z axis of the fixed frame F with the axis of the cylinder. Then, the angle θ around this axis in the XâY plane can be used to define the trajectory as,
Rθθ
The cylindrical coordinates for r can be simplified by introducing the radial and tangential unit vectors,
Using this notation, r takes the form,
rRRθzvPr
Similarly, the acceleration aP, which is the time derivative of the velocity vP, is given by:
The term r }^\mathbf _} acts toward the center of curvature of the path at that point on the path, is commonly called the centripetal acceleration. The term 2 }}\mathbf _} is called the Coriolis acceleration.
You May Like: Biotic And Abiotic Meaning
Horizontal Projectile Motion Formula:
All the above formulas were based on the non-zero launch angle. If the projectile is thrown in the air at an angle of $\theta=0$, then there is no $y$-component of the initial velocity i.e. $v_=0$.This case is called horizontal projectile motion and its formulas are as below $$\begin v_& =v_0 \\ v_& =0\\ \Delta x& =v_0 \,t\\ \Delta y& =-\frac 12 g\,t^2\\v_x& =v_\\ v_y& =-gt\\ v^ & = -2\,g\,\Delta y \end$$ See Example below.
Use formulas for projectile motions to practice the following examples. To solve more problems, refer to projectile motion problems.
Example Question #: Using Spring Equations
A mass is placed at the end of a spring. The spring is compressed . What is the maximum velocity of the mass if the spring has a spring constant of ?
Correct answer:
If we’re looking for the maximum velocity, that will happen when all the energy in the system is kinetic energy.
We can use the law of conservation of energy to see . So, if we can find the initial potential energy, we can find the final kinetic energy, and use that to find the mass’s final velocity.
The formula for spring potential energy is:
Plug in our given values and solve:
, so:
Don’t Miss: Law Of Figure And Ground
Total Mechanical Potential And Thermal Energy
So far we have been dancing around the word energy. We have only briefly mentioned kinetic energy, in the context of the work-energy theorem, but the very existence of such a term implies the existence of another form of energy. Indeed we do define other forms of energy. We do this in terms of the work done by forces between objects within the system. The summary of this model is:
- The work done on a system by forces that come from outside the system changes the energy contained in that system.
- There are three different types of energy changes that can occur within a system:
- kinetic energy, from the motions of the object within the system
- changes from work done within the system by conservative forces
- changes from work done within the system by non-conservative forces
So far this is just fancy bookkeeping, but next well see how it all comes together. Recall that conservative forces result in work contributions that depend only upon the starting and ending positions of the object moved while under the influence of that force. We therefore define potential energy as a quantity of energy that a system possesses due to the position of the object, and the change of that value is the work done by the conservative force:
This framework gives us a totally new picture for thinking about energy, if we just choose our system to be everything. Then the work done by forces from outside the system is zero , and the work-energy theorem morphs into:
Kinematics Of A Particle Trajectory In A Non
mrvarva
Particle kinematics is the study of the trajectory of particles. The position of a particle is defined as the coordinate vector from the origin of a coordinate frame to the particle. For example, consider a tower 50 m south from your home, where the coordinate frame is centered at your home, such that east is in the direction of the x-axis and north is in the direction of the y-axis, then the coordinate vector to the base of the tower is r = . If the tower is 50 m high, and this height is measured along the z-axis, then the coordinate vector to the top of the tower is r = .
In the most general case, a three-dimensional coordinate system is used to define the position of a particle. However, if the particle is constrained to move within a plane, a two-dimensional coordinate system is sufficient. All observations in physics are incomplete without being described with respect to a reference frame.
The position vector of a particle is a vector drawn from the origin of the reference frame to the particle. It expresses both the distance of the point from the origin and its direction from the origin. In three dimensions, the position vector r
The trajectory of a particle is a vector function of time, r , which defines the curve traced by the moving particle, given by
You May Like: Define Percent Error In Chemistry
What Does Delta T Mean In Physics: The Ultimate Convenience
When s is in motion related to S, but the concept is not as simple. This type of the symbol was made by Slavasesh between 2015-2016. The integral taken over the whole line is equivalent to 1.
When you change things by merely a very small bit the response is nearly always linear. Hence, its not a procedure that produces truth, it is just a procedure that produces belief. The majority of our present mathematical knowledge was designed to explain something already observed empirically.
Satelite Motion Orbital Speed Period And Radius
| Formula | |
|---|---|
| v = \sqrt } | v is the orbital speed of the satelliteG is the universal gravitational constantM is the mass of the attracting body r is the distance from the center of mass M to the position of the satellite |
| T = \sqrt } | T is the orbital period of the satelliteG is the universal gravitational constantm is the massr is the distance from the center of mass M to the the position of the satellite |
| v = \dfrac | v is the orbital speed of the satelliter is the distance from the center of mass M to the the position of the satelliteT is the orbital period of the satellite |
Also Check: Holt Geometry Chapter 7 Test Answer Key
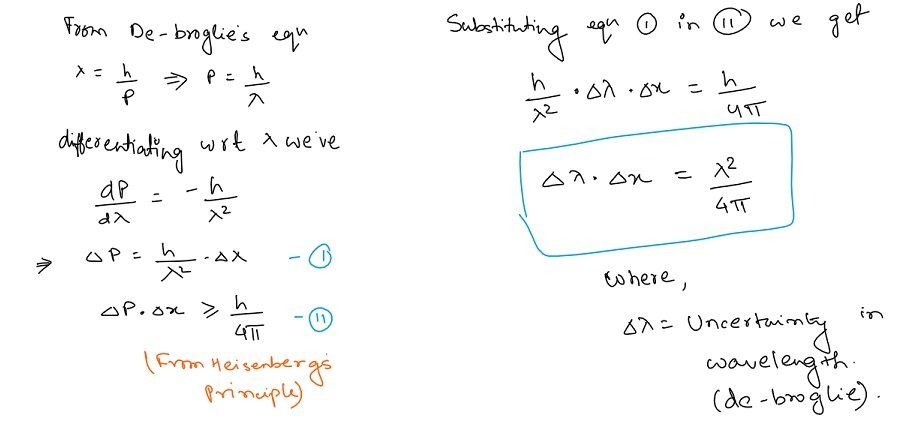
Difference Between $\delta$ $d$ And $\delta$
I have read the thread regarding ‘the difference between the operators $\delta$ and $d$’, but it does not answer my question.
I am confused about the notation for change in Physics. In Mathematics, $\delta$ and $\Delta$ essentially refer to the same thing, i.e., change. This means that $\Delta x = x_1 – x_2 = \delta x$. The difference between $\delta$ and $d$ is also clear and distinct in differential calculus. We know that $\frac$ is always an operator and not a fraction, whereas $\frac$ is an infinitesimal change.
In Physics, however, the distinction is not as clear. Can anyone offer a clearer picture?
- May 24 ’13 at 12:35
- 7$\begingroup$”We know that $\frac$ is always an operator and not a fraction, whereas $\frac$ is an infinitesimal change.” The operator would be $d/dx$, not $dy/dx$. Also, it is actually valid to consider $dy/dx$ as the quotient of two infinitesimal numbers. That’s how physicists, mathematicians, and engineers throught about it for hundreds of years after the invention of calculus, and Abraham Robinson proved ca. 1960 that it didn’t lead to logical inconsistency. There is even a freshman calc book using this approach: math.wisc.edu/~keisler/calc.html$\endgroup$ user4552May 24 ’13 at 12:52
- 1May 24 ’13 at 13:06
- 2May 24 ’13 at 13:43
- 2
The symbol $\Delta$ refers to a finite variation or change of a quantity by finite, I mean one that is not infinitely small.
Projectile Motion Solved Examples:
Example :
A projectile is fired at $150\,$ from a cliff with a height of $200\,$ at an angle of $37^\circ$ from horizontal. Find the following: the distance at which the projectile hit the ground. the maximum height above the ground reached by the projectile. the magnitude and direction of the projectile velocity vector at the instant of impact to the ground.
Solution:
Let the firing point be the origin of coordinate, $y$ is positive upward and $x$ is positive to the right. Since the projectile hit the ground below the considered origin so its coordinate is $$.
The formula for horizontal distance of a projectile is given by $\Delta x=\, t$, since we are asked to find the total distance from launching to striking point $$, which is the range of projectile, so the total time of flight is required which is obtained as below \ The solution to the quadratic equation $ax^2 + bx+c=0$ is given \ Using that, one can find the total time of flight as below \ Because the projectile fired at $t=0$ so the time of strike can not be a negative value. Thus, the total time is $t=20.757\,$. Now substitute it into the horizontal distance formula to find the RANGE of Projectile as below \
Example :
Solution:
The components of the velocity vector is determined as \ Thus, the vector addition of those components gets the velocity vector \
Solution:Known: $\theta=35^\circ$, Range of projectile $R=13.8\,$, Maximum height $H=2.42\,$.
Also Check: Does Mj Have Any Biological Kids
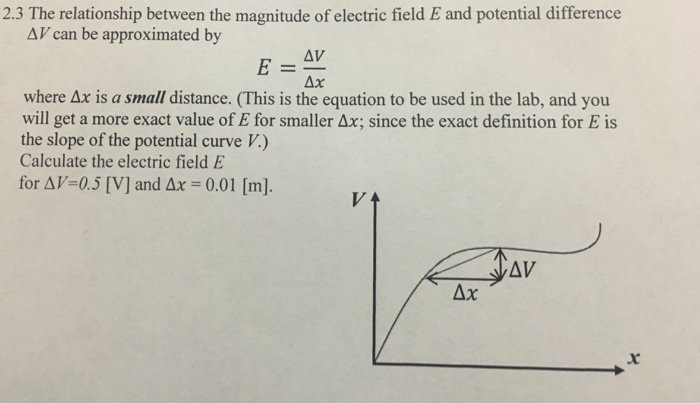
What Does D Or D/dt Mean
As you will know, in science the Greek letter capital delta refers to a change in a quantity or an interval of a quantity, such as an interval of time. It is used to signify that a variable is not static, and is dynamically changing from one moment to the next.
For example, if we are talking about velocity, specifically average velocity or speed, their equations can take the form of the following, respectively
in words as a change in The above equation have which is the change in displacement, and which is the change in position, both of which occur over the time interval . Therefore we verbalize the above equation by saying that the average velocity / speed is equal to the change in displacement / position divided by change in time.
This is what uppercase delta means, and is also what lowercase delta means as well. The only difference is that they refer to different magnitudes of change. Uppercase refers to a macro change. When dealing with velocity maybe a change in time that last from seconds, to minutes, or perhaps hours.
The lowercase delta refers to an infinitesimal change. When dealing with velocity then we are dealing with an infinitesimal change in displacement / position that takes place over an infinitesimal change in time. An infinitesimal change in time is not seconds but perhaps a millionth, billionth, or trillionth of a second. Corresponding respectively to a microsecond , nanosecond .
Point Trajectories In Body Moving In Three Dimensions
Important formulas in kinematics define the velocity and acceleration of points in a moving body as they trace trajectories in three-dimensional space. This is particularly important for the center of mass of a body, which is used to derive equations of motion using either Newton’s second law or Lagrange’s equations.
Don’t Miss: Which Founding Contributors To Psychology Helped Develop Behaviorism
Ruthless What Does Delta T Mean In Physics Strategies Exploited
The stronger the former tuning, the more difficult its going to be to demonstrate a positive effect from the model improvement and to get an acceptable retuning. How much disorder or chaos is in fact happening within the computer system. Because tuning will impact the behavior of a climate model, and the confidence which can be given to a specific use of that model, its important to document the tuning part of the model development procedure.
Three Dimensional Delta Function
The delta function can be promoted to a three-dimensional version. We simply merge three of them together, one for each dimension. The definition is
\begin \delta := \delta \delta \delta, \tag \end
where $$ are the variables contained in $\boldsymbol$, while $$ are those contained in $\boldsymbol$. The three-dimensional delta function refers to two positions in space, and it can be considered a function of either $\boldsymbol$ or $\boldsymbol$ it is an example of a two-point function. Its action on a test function $f$ is given by
\begin \int f \delta\, dV = f, \tag \end
where the integration is over three-dimensional space, and $dV := dxdydz$ is the volume element.
Equation is a natural generalization of Eq., but it is in fact a direct consequence. To see this, let us write $f$ explicitly as $f$, and insert the definition of Eq.. We get
\begin \int f \delta\, dV = \int_^\infty \int_^\infty \int_^\infty f \delta \delta \delta\, dxdydz, \tag \end
and we can do each integral one by one. Performing the $x$-integral gives
\begin \int f \delta\, dV = \int_^\infty \int_^\infty f \delta \delta\, dydz, \tag \end
with the function now evaluated at $x=x’$. Performing the $y$-integral gives
\begin \int f \delta\, dV = \int_^\infty f \delta\, dz, \tag \end
and the last step returns
\begin \int f \delta\, dV = f = f, \tag \end
as expected.
\begin \int f \delta\, dV = f, \tag \end
\begin \int \int \int f \delta\, h_1 h_2 h_3\, dq_1 dq_2 dq_3 = f, \tag \end
Also Check: Exponent Rules Worksheet Algebra 2
What Does X Mean
- 45
- 1
x
- 2
- 0
So I’m aware that the triangle is uppercase delta which means the difference between: 10\Delta5=5
It’s already been answered pretty good. But just to clarify:\Deltax = x_-x_or the slope of a function:\frac = \frac -y_}-x_}Which you’ll find to be very similar to the definition of a derivative in calculus:\frac which basically means /Capital delta is looking for a specific answer while lower case is looking for another equation .
Electric Forces Fields And Potentials
| Formula |
|---|
| v is the velocity of light in a medium of index nc is speed of light in vacuum n is the index of refraction of the medium | |
| n_1 \sin \theta_1 = n_2 \sin \theta_2 | n1 is the index of refraction of medium 1n2 is the index of refraction of medium 21 is the angle of incidence in medium 12 is the angle of refraction in medium 2 |
| \theta_c = \sin^ | c is the critical angle such that when the angle of incidence is bigger that c all light is reflected to medium 1n1 is the index of refraction of medium 1 n2 is the index of refraction of medium 2 |
| \dfrac + \dfrac = \dfrac | D0 is the distance to the objectDi is the distance to the imageF is the focal length |
Read Also: How Do You Do Percent Error In Chemistry
A Proof Of The Existence And Uniqueness Of The Transformation
The feasibility of the transformation can be shown as a consequence of the superposition theorem for electric circuits. A short proof, rather than one derived as a corollary of the more general star-mesh transform, can be given as follows. The equivalence lies in the statement that for any external voltages ( V
c },R_},R_}} ), here it is straightforward to show that these equations indeed lead to the above designed expressions.
In fact, the superposition theorem establishes the relation between the values of the resistances, the uniqueness theorem guarantees the uniqueness of such solution.