What Does N Equal In Algebra

What Is Actually Going On With What Does N Equal In Math

Both sides of the equation corresponds to a side of the balance. You should not presume that your mean is going to be one of your initial numbers. To locate these values, you begin by finding the very first derivative. An expression that comes with a variable is known as an algebraic expression. The equation evaluates the period of the string with respect to its wavelength. Weve found the amount needed to improve our sum in order to acquire a mean of 90 with 6 terms.

Thus, dont be worried about that now, we will get to that later. Youve got to differentiate between whos gifted and who isnt. Suppose we have to fix this. This makes it simple to remember.

Or * Or Multiplication

These symbols have the same meaning commonly × is used to mean multiplication when handwritten or used on a calculator 2 × 2, for example.

The symbol * is used in spreadsheets and other computer applications to indicate a multiplication, although * does have other more complex meanings in mathematics.

Less commonly, multiplication may also be symbolised by a dot . or indeed by no symbol at all. For example, if you see a number written outside brackets with no operator , then it should be multiplied by the contents of the brackets: 2 is the same as 2×.

See our page on Multiplication for more.

Absolute Value Examples And Equations

The most common way to represent the absolute value of a number or expression is to surround it with the absolute value symbol: two vertical straight lines.

• |6| = 6 means the absolute value of 6 is 6.
• |6| = 6 means the absolute value of 6 is 6.
• |2 x| means the absolute value of the expression 2 minus x.
• |x| means the negative of the absolute value of x.

The number line is not just a way to show distance from zero it’s also a useful way to graph equalities and inequalities that contain expressions with absolute value.

Consider the equation |x| = 2. To show x on the number line, you need to show every number whose absolute value is 2. There are exactly two places where that happens: at 2 and at 2:

Now consider |x| > 2. To show x on the number line, you need to show every number whose absolute value is greater than 2. When you graph this on a number line, use open dots at 2 and 2 to indicate that those numbers are not part of the graph:

In general, you get two sets of values for any inequality |x| > k or |x| k, where k is any number.

Now consider |x| 2. You are looking for numbers whose absolute values are less than or equal to 2. This is true for any number between 0 and 2, including both 0 and 2. It is also true for all of the opposite numbers between 2 and 0. When you graph this on a number line, the closed dots at 2 and 2 indicate that those numbers are included. This is due to the inequality using instead of < .

Recommended Reading: What Does Pcr Stand For In Biology

< Less Than And > Greater Than

This symbol < means less than, for example 2 < 4 means that 2 is less than 4.

This symbol > means greater than, for example 4 > 2.

These symbols mean less than or equal to and greater than or equal to and are commonly used in algebra. In computer applications < = and > = are used.

These symbols are less common and mean much less than, or much greater than.

+ Addition Plus Positive

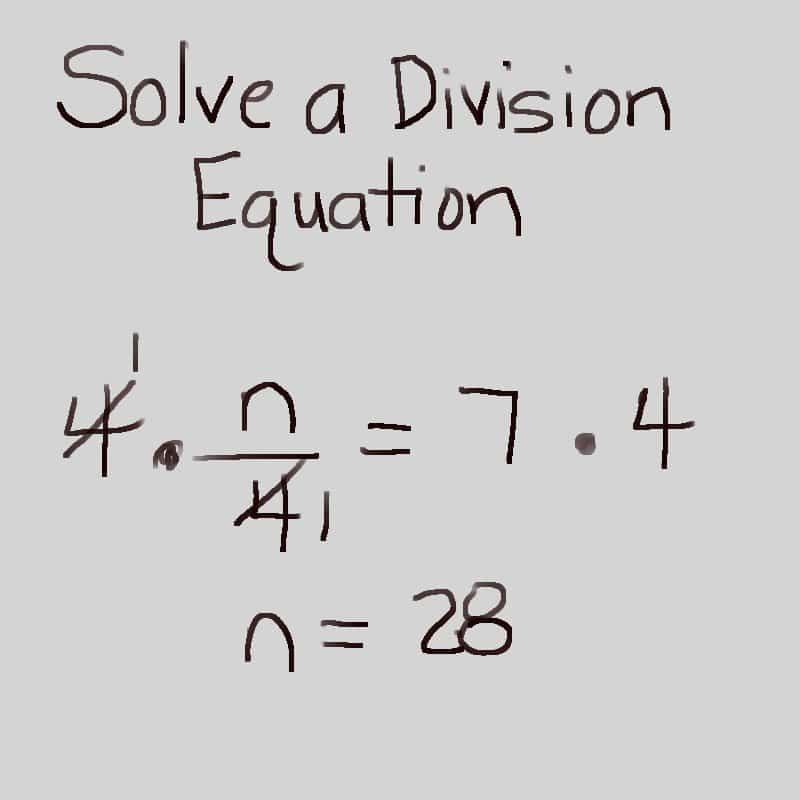
The addition symbol + is usually used to indicate that two or more numbers should be added together, for example, 2 + 2.

The + symbol can also be used to indicate a positive number although this is less common, for example, +2. Our page on Positive and Negative Numbers explains that a number without a sign is considered to be positive, so the plus is not usually necessary.

See our page on Addition for more.

Read Also: Do You Have To Take Chemistry In College

How Do I Construct A Real Number Line

Here are three steps to follow to create a real number line.

Choose any point on the line and label it 0. This point is called the origin.

Now that you have created a number line, it is time see how points on a number line are defined.

Real Numbers

A real number is any number that is the coordinate of a point on the real number line.

What Is N Called In Math

List of Mathematical Symbols R = real numbers, Z = integers, N=natural numbers, Q = rational numbers, P = irrational numbers. Page 1. List of Mathematical Symbols.

What does n equal in algebra?

In an equation, N represents a specific number, not any number. N + 9 = 12 means N is a number which, when added to 9, must give the answer 12. So N can only be the number 3 because only 3 + 9 is equal to 12.

What does the letter n mean in math?

A variable is a letter or symbol that stands for a number and is used in mathematical expressions and equations. In an arithmetic sequence, which is a list of numbers that follow a pattern, n is a variable representing the number of the term to find.

Read Also: What Is Mgh In Physics

What Does The Notation N* Mean

Are there any conventions about the use of $n^*$ as notation of a variable? I have seen it for the first time here.

• 1$\begingroup$typically it is used to show that something is new or different. Yet maintains a lot of the aspects of the old.$\endgroup$Apr 24, 2011 at 23:19
• 2$\begingroup$In the post you linked to it’s already been defined as the function described in the post. In general it means a lot of things depending on context.$\endgroup$Apr 24, 2011 at 23:41
• $\begingroup$Huh, the original link broke. Oh well, that’s life.$\endgroup$

There’s no general convention. The use in the webpage you cited certainly isn’t widely known or used.

Generally, mathematicians like to use adornments to variable names to indicate a particular operation. Mathematicians especially like the use of adornments when the operation is a duality relation.

Some examples of adornments that signifies a duality relation include:

• $p$ and $\bar$ for complex conjugation
• $A$ and $A^t$ for matrix transposition
• $A$ and $A^*$ for operator adjoints
• $f$ and $\hat$ for the Fourier transformation
• $\omega$ and $^*\omega$ for the Hodge dual of forms

Aside from some of the uses of the star adornment which are already mentioned in other answers, there is one other use that is common in mathematical analysis, especially in conjunction with the study of partial differential equations :

What Is Letter N In The Alphabet

N, or n, is the 14th letter in the modern English alphabet and the ISO basic Latin alphabet. Its name in English is en , plural ens.

What is the letter N in Greek?

Nu or ny is the 13th letter of the Greek alphabet. In the system of Greek numerals it has a value of 50. It is derived from the ancient Phoenician language nun . Its Latin equivalent is N, though the lowercase resembles the Roman lowercase v .

What does a letter symbolize?

The letter is absolutely applied as a symbol of communication. Letters can symbolize self-knowledge, insight and perception. Traditionally they are interpreted as unfavorable or unpleasant, just a letter that informs about someones death can stand for good news.

Previous Post

Also Check: College Algebra Graphs And Models 4th Edition

Introduction: Connecting Your Learning

Mathematics is commonly referred to as the universal language. With the overwhelming popularity of social media, this is becoming increasingly clear. You cannot communicate with others from various walks of life without the common language of mathematics driving your Internet connection, moving satellites, or translating words.

Furthermore, people cannot map the earth from smartphones without computer programmers to generate mathematical algorithms to provide this technology. If you choose to pursue a career in information technology, whether it is in security, networking, mobile applications, or geospatial technology, you will need a certain level of mathematical knowledge.

In this lesson, you will learn how real numbers are ordered, how many categories of numbers exist, and mathematical symbolism that allows you to quickly compare or categorize numbers.

Whats Truly Happening With What Does N Equal In Math

These models help prepare them for algebra and consider the structure of issues at quite a deep level. Rather than considering Leibnizs law as a real statement that may be proven from the normal laws of logic , it may also be taken as the definition of equality. This sort of thinking is essential in algebra and it might enrich the learning of mathematics. Equations often contain terms aside from the unknowns. In fact they are not equal to anything.

Although it was discovered 350 years back, scientists continue to discover new examples of Eulers number in nature. Our findings most likely dont generalize outside this subject. The fundamental properties that students use to perform arithmetic operations actually supply the foundation for the majority of the symbolic manipulations in algebra. Stop by the TRC to get the latest information about science professional improvement.

Generally the Rate is speed but it might be anything per anything. A step process often aids in tackling a word issue. Inaccurate or only partially true definitions might get the job done for some time, but they eventually quit working, while in addition wreaking havoc on the way.

But all youve got to do is simply get everything on a single side. These arent restricted to boys. The subtext, obviously, is that large quantities of American kids are just not born with the capacity to solve for x.

Read Also: What Is E Called In Math

What Does I Equal In Algebra

Answer:

It was invented by mathematicians back then when while having problems finding the roots of some cubic equations and they noted the fact that some numbers that it is said imaginary today cannot be represented on the x-axis, so why not use the y-axis to represent them and thus gave rise to the concept of square roots of negative number i.e. imaginary numbers.

It is denoted by i, where the value of i is considered as . Any real number when multiplied by an imaginary number will result in an imaginary number. For example 5 × = or 5i. Imaginary numbers, as its name suggests are not actually imaginary. They do exist. Let us take an example:

Let suppose solving a quadratic equation x2 = -4. In the above equation, one cant find the root of -4, which implies that there are no real roots i.e the parabola does not cut the x-axis as shown in the diagram.

Write the above equation as x2 = -1 × 4. Now, we know the square root of 4 is +2 and -2.

But the square roots of -1 is not known, so mathematicians invented a new number as and named it i Now one can solve the above equation by assuming as i and get the respective roots as +2i and -2i.

Evolution of Imaginary Numbers

Real-life Example of Imaginary number

Considering the above example, we can say that r . r = -1. . After taking a 90° turn, the new velocity of the man will become X.r, where r = .

Representation of Imaginary Numbers

Question 1: Which of the following among the given number are imaginary numbers?

Lesson : Developing The Concept

Materials: Index cards or digital “cards” that can be distributed among the class

Standards:

• Understand the absolute value of a rational number as its distance from 0 on the number line.

Preparation: Make cards for I HaveWho Has?

• Say:Remember that absolute value is the distance that a number is from 0, no matter which direction.
• Ask:Can someone write an equation that means “24 is the absolute value of the number that is 6 less than x?”The equation, 24 = |x 6|, represents the situation. You may need to repeat the equation several times, slowly, as students try to parse it out.
• Ask:What can be the value of the expression inside the absolute value symbols?It is natural to show that x 6 can have a value of 24. Help students see that the expression can also have a value of 24. If necessary, remind them of your previous discussion about directed distance from zero as opposed to absolute distance from zero.
• Ask:If the expression can have a value of 24 or 24, what values can x have?Have students try to find possible values for x themselves at first. Then have them compare what they found, and facilitate a discussion around different strategies they used.If x = 30, then x 6 = 24. If x = 18, then x 6 = 24. There are two possible values for x: 30 and 18.
• Repeat the last three questions using a variety of absolute value expressions:

  |13 x| = 14 |25 + x| = 25 42 = |2x| 1 = |x/36| 0 = |36/x|

Wrap-Up and Assessment Game

Recommended Reading: Who Is Kaepernick’s Biological Father

Cite This Page As Follows:

“What do the letters R, Q, N, and Z mean in math?” eNotes Editorial, 7 Sep. 2010, https://www.enotes.com/homework-help/what-do-the-letters-r-q-n-and-z-mean-in-math-195625.Accessed 18 Sep. 2022.

Who are the experts?Our certified Educators are real professors, teachers, and scholars who use their academic expertise to tackle your toughest questions. Educators go through a rigorous application process, and every answer they submit is reviewed by our in-house editorial team.

The letters R, Q, N, and Z refers to a set of numbers such that:

R = real numbers includes all real number

Q= rational numbers

N = Natural numbers

z = integers

Multiplying And Dividing Negative Numbers

There are two rules for multiplying and dividing numbers:

• If you’re multiplying or dividing two numbers that are either both positive or both negative, your result will be positive.
• If you’re multiplying or dividing a positive number and a negative number, your result will be negative.

That’s it! You multiply or divide as normal, then use these rules to determine whether the answer is positive or negative. For instance, take this problem, -3-4. 3 4 is 12. Because both numbers we multiplied were negative, the answer is positive: 12.

-3 -4 = 12

On the other hand, if we were to multiply 3 -4, we’d get a different answer:

3 -4 = -12

Again, 3 4 is 12. But because one of our multiples is negative and the other is positive, our answer must also be negative: -12.

It works the same way for division. -40 / -10 is 4 because –40 and -10 are both negatives. However, -40 / 10 is -4 because one number is negative and the other is positive.

Read Also: Why Is New Math Better

What Does N Equal In Math Options

Sets can be equal to one another or equivalent. Flexible Grouping The secret to flexible grouping is it is indeed flexible. Singapore Math presents several different alternatives for kindergarten. Singapore Math presents several distinct editions of its homeschool math curriculum, and supplemental books.

Ask Dr. Math If youve got a math question, this website is for you. After youve purchased the Home Instructors Guide, check the front for the complete collection of what you will need. Because students often locate these courses more engaging also, they are very likely to find out more in them. Allow students to pick the numbers.

Positive Numbers Negative Numbers

Real numbers whose graphs are to the right of 0 are called positive real numbers, or more simply, positive numbers. Real numbers whose graphs appear to the left of 0 are called negative real numbers, or negative numbers.

The number 0 is neither positive nor negative.

Recommended Reading: What Are The Basic Principles Of Chemistry

The Order Of Math Operations

When you are given a mathematical expression or an equation, the order in which mathematical operations are performed is very important. The rules for this are quite simple. Consider the following example:

2 + * 32 + 4* + 10

At first this may look daunting, but it is really quite simple. The rules are: summarized in the table below.

Algebraic Properties Satisfied By The Natural Numbers

The addition and multiplication operations on natural numbers as defined above have several algebraic properties:

• Closure under addition and multiplication: for all natural numbers a and b, both a + b and a × b are natural numbers.
• Associativity: for all natural numbers a, b, and c, a + = + c and a × = × c.
• Commutativity: for all natural numbers a and b, a + b = b + a and a × b = b × a.
• Existence of identity elements: for every natural number a, a + 0 = a if and a × 1 = a.
• If the natural numbers are taken as “excluding 0”, and “starting at 1”, then for every natural number a, a × 1 = a. However, the “existence of additive identity element” property is not satisfied

You May Like: Kuta Software Infinite Algebra 1 Adding Subtracting Rational Expressions