What Does Variation Mean In Math

Example 1: Direct Variation Relationship

A professional sports team notes that the ambient crowd noise at home games is directly proportional to the attendance at those games. During one game, the cheering of a maximum capacity crowd of 75,000 fans averages 90 decibels. Identify the constant of proportionality k.

Solution

Let a represent attendance and n represent the noise generated by that population. If n varies directly with a, then n = ka. Substitute n = 90 and a = 75000 into the equation and solve for k.

n = ka

Role In The Curriculum

The National Council of Teachers of Mathematics states in Principles and Standards for School Mathematics :

A major goal in is to develop students facility with using patterns and functions to represent, model, and analyze a variety of phenomena and relationships in mathematics problems or in the real world. With computers and graphing calculators to produce graphical representations and perform complex calculations, students can focus on using functions to model patterns of quantitative change. Students should have frequent experiences in modeling situations with equations of the form y = kx, such as relating the side lengths and the perimeters of similar shapes. Opportunities can be found in many other areas of the curriculum for example, scatterplots and approximate lines of fit can model trends in data sets.

The equation y = kx is the general equation for direct variation. This equation represents a linear function with slope k that passes through the origin. The PSSM also suggests that he study of patterns and relationships in the middle grades should focus on patterns that relate to linear functions, which arise when there is a constant rate of change.

What Does Variation Mean In Math Terms

There are different types of variation in math – directvariation, inverse variation, and joint variation for a start.

Direct variation is just simply that x and y vary directly. Whatthis means is that they do the same thing – as x increases so doesy, or as x decreases so does the value of y.

In general the formula for direct variation is y=kx where k isthe constant of variation.

Inverse variation is when x and y do the opposite of each other.So as x increases, y decreases or as x decreases the value of yincreases. One fun example of where this happens in real life iswith Ramen Noodles – the less money people make the more RamenNoodles they buy. We would say that people’s income and the amountof Ramen Noodles they buy vary inversely.

In general the formula for inverse variation is y = k/x whereagain k is the constant of variation.

Joint variation is when you have three variables that arerelated. The general formula for joint variation is y=kxz where zis just a third variable and k is still the constant ofvariation.

Also Check: Geometry Basics Angle Addition Postulate Worksheet Answers

Procedural Variation: Whats The Same Whats Different And What Do You Notice

We can use procedural variation to highlight patterns within a set of questions that bring about a critical learning point or object of learning. Say we wanted to draw students attention to one of the field axioms of multiplication distributivity so that they can employ it at will when dealing with any multiplication. We may present this in the following way:

The incorrect way to go about this would be to treat this as a worksheet, in which you deliver an input and tell the students to crack on and complete it. There would be no method to that madness, and the opportunities for bringing out new and previous learnt relationships between the numbers would likely fall by the wayside for all students, or would only be found by those who are high attaining in mathematics.

Rather, a more controlled approach should be taken. You should ask students to complete the first two questions and then ask them, what is the same, what is different and what do you notice? This will provide the opportunity to pick up on what the design of these minimally different questions is attempting to draw out.

Procedural variation steps

Firstly, you would want students to notice the relationship between the multiplicand from the given statement and the combination of the multiplicands from the first two equations . Students will be drawn to the fact that they all total the same and that the product is also going to be 96.

Problem solving in procedural variation

Variation Theory examples KS1

Example : Direct Variation Application

In a downtown office building, the monthly rent for an office is directly proportional to the size of the office. If a 450-square-foot office rents for $1350 per month, then what is the rent for an 800-square-foot office?

Solution

Given that the monthly rent is directly proportional to the office size, then the rent, R, varies directly with the area of the office, A. Since 450-square-foot office rents for $1350 per month, substitute to the direct variation formula and find k.

R = kA

1350 = k

k = 3

Now that we have the value of k, which is 3, then write the new equation incorporating the value of k. Then, to get the rent for an 800-square-foot office, insert 800 into the new formula.

R = 3A

Therefore, an 800-square-foot office rents for $ 2400 per month.

Don’t Miss: 4.5 Practice B Geometry Answers

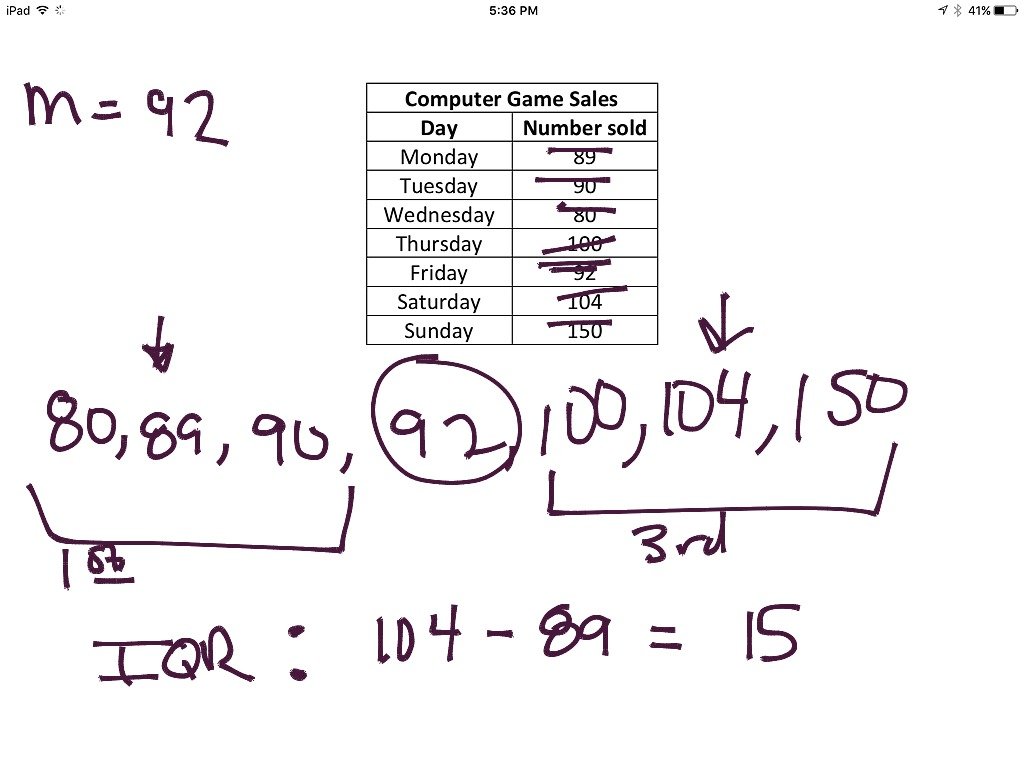
Center And Variation Of Data

Given a numerical data distribution, we can answer questions about the central tendency of the data and its variation.

We can use different measures like to represent the center of the data with a single number.

The variation can also be expressed with a single number, most simply by finding the , or difference between the highest and lowest values. It can also be expressed using the or .

For example, in the dot plot below, most of the data is clustered in the range 9 , and the mean is about 8.2

, and the standard deviation is about 3.8 .

Another way to express the central tendency and variation of a numerical data set is with a .

Population Variance And Sample Variance

Real-world observations such as the measurements of yesterday’s rain throughout the day typically cannot be complete sets of all possible observations that could be made. As such, the variance calculated from the finite set will in general not match the variance that would have been calculated from the full population of possible observations. This means that one estimates the mean and variance from a limited set of observations by using an estimator equation. The estimator is a function of the sample of nobservations drawn without observational bias from the whole population of potential observations. In this example that sample would be the set of actual measurements of yesterday’s rainfall from available rain gauges within the geography of interest.

Firstly, if the true population mean is unknown, then the sample variance is a biased estimator: it underestimates the variance by a factor of / n correcting by this factor is called Bessel’s correction. The resulting estimator is unbiased, and is called the sample variance or unbiased sample variance. For example, when n = 1 the variance of a single observation about the sample mean is obviously zero regardless of the population variance. If the mean is determined in some other way than from the same samples used to estimate the variance then this bias does not arise and the variance can safely be estimated as that of the samples about the mean.

Recommended Reading: Kuta Software Infinite Algebra 1 Solving Absolute Value Equations

What Is Variation Theory In Primary Maths

Variation Theory is a general theory of learning that is used predominantly in mathematics teaching and pedagogy. It emphasises a concepts essential features by focusing on what is kept the same and what changes, which offers the opportunity to make meaningful connections.

FREE Crib Sheet for Primary School Staff Meetings

How To Find Coefficient Of Variation

The relative standard deviation or CV, is a conventional measure of the dispersion of a probability distribution or frequency allocation. If the value of the coefficient of variation is lower it states that the data has less variability and high stability.

The basic steps involved in the calculation is:

• Review the given sample data.
• Compute the standard deviation separately using the formula discussion in the previous section.
• Next, obtain the mean individually by the formula.
• Lastly, insert the values in the CV formula i.e. equal to\

Let us understand how to find the coefficient of variation with an example.

Question: Find the coefficient of variation if the Mean is 50.1 and the standard deviation is 11.2.

Solution:

\\times100\%\) \\times100\%\) \

You May Like: What Does The Denominator Tell You

Variance Vs Standard Deviation

The standard deviation is derived from variance and tells you, on average, how far each value lies from the mean. Its the square root of variance.

Both measures reflect variability in a distribution, but their units differ:

• Standard deviation is expressed in the same units as the original values .
• Variance is expressed in much larger units

Since the units of variance are much larger than those of a typical value of a data set, its harder to interpret the variance number intuitively. Thats why standard deviation is often preferred as a main measure of variability.

However, the variance is more informative about variability than the standard deviation, and its used in making statistical inferences.

Math Review Of Direct Inverse Joint And Combined Variation

Overview:

Equations that describe the relationship between two variables in a sentence express the variation between those variables. Examples of types of variation include direct, inverse, joint, and combined variation.

What Is Direct Variation?

In direct variation, as one variable is multiplied by a constant and increases, another variable also increases. Suppose Jane works at McDonalds and is paid $9.35 per hour. Her total wages vary directly with the amount of hours she works. If she works 1 hour, her gross wages are $9.35, and if she works 2 hours her gross wages are $18.70. If she works 8 hours, her wages are $74.80. If the hours she works are plotted on the x axis against her wages on the y axis, the resulting line is a straight line showing direct variation.

What Is Inverse Variation?

Inverse variation is a relationship between variables so that as one variable decreases the other variable increases. The equations expressing inverse variation take the form xy = k, where k is a constant, as well as y = k/x.. For example, the current c varies inversely with the resistance in ohms r. When the current is 40 amps, the resistance is 12 ohms. When the current is 24 amps, the resistance is 20 ohms. If the current is plotted on the x axis, and the resistance is plotted on the y axis, the graph is in 2 separate curves called a hyperbola.

What Is Joint Variation?

What Is Combined Variation?

Read Also: My Hrw Algebra 1

Example : Writing A Direct Variation Equation

If it is known that y varies directly as x and that y = 32 and x = 4, find the variation constant and the equation of variation.

Solution

To express the statement y varies directly as x, we write y=kx. Therefore, by substituting the given values in the derived equation we come up with the following equation.

32 = 4k

The variation constant is 8 and the equation of variation is given by y = 8x.

Homogeneity Of Variance In Statistical Tests

Variance is important to consider before performing parametric tests. These tests require equal or similar variances, also called homogeneity of variance or homoscedasticity, when comparing different samples.

Uneven variances between samples result in biased and skewed test results. If you have uneven variances across samples, non-parametric tests are more appropriate.

Recommended Reading: Theory Of Everything 2 Song

Example : Mortgage Payments As Direct Variation Example

The monthly payment P on a mortgage varies directly with the amount borrowed B. If the monthly payment on a 30-year mortgage is $6 for every $1000 borrowed, find a formula that relates the monthly payment P to the amount borrowed B for a mortgage with these terms. Then, find the monthly payment P when the amount borrowed B is $120,000.

Solution

Take note that P varies directly with B. Write the equation translating this mathematical statement. Then, find the variation constant k given the first condition where the monthly payment on a 30-year mortgage is P = $6 for every B = $1000 borrowed.

P = kB

6 = k

k = 0.006

Solve the value of P given the new B = $120,000 and obtained value of k = 0.006.

P = kB

P = 0.006

P = $720

The figure below illustrates the relationship between the monthly payment P and the amount borrowed B.

Direct Variation Graph Example

Therefore, the monthly payment P when the amount borrowed B is $120,000 is $720.

Guidelines For Solving A Direct Variation Equation

Don’t Miss: Algebra 2 Chapter 7 Test Answers

Solved Examples For Coefficient Of Variation

In statistics, the terms like coeff of variation, variance and standard deviation are best understood with practical solved examples. As you have seen all the related formulas let us now move towards some solved examples to understand the application of the formula.

Solved Example 1: If coefficient of variation is \ and arithmetic mean is\, then standard deviation is ?

Solution:

That is

SD = 15x

Solved Example 2: For the given data set 1, 0, 2, 3, 1, 1, 15, 1, 3. Find the value of the coeff. of variation?

Solution:\

Let us start our calculation with the mean:

Mean = /9 = 27/9 = 3

Mean Deviation about the mean= Subtract mean from each given data set values

For example, 0 3 = 3

1 3 = 2, 2 3 = 1, 3 3 = 0, 15 3 = 12

M.D = /9 = 24/9 = 8/3

In the above steps we calculated the value of Mean Deviation = 3, 2, 2, 2, 2, 1, 12

The value of Variance = \

Standard Deviation = \

Now substitute the obtained value in the formula:

Coeff. of variation=\}\times100\)=144.871

Check out this article on Elementary Statistics.

Solved Example 3: If the variance of a distribution is 81 and the coefficient variation is 30%, find the mean.

Solution: Given

Variance = 81 and CV = 30%

We know that, \

S.D=\

As per the formula, \

Mean = 30

What Is Coefficient Of Variation

In the statistics and probability approach, the coeff. of variation or CV is a measure of scattering/dispersion of given information details around the mean value. In mathematics, a coefficient is defined as an integer that is multiplied with the variable of a single element or the terms of a polynomial. It is usually a number, but sometimes may be followed by a letter in an expression. For example: \.

Here x denotes the variable and a and b are the coefficients of the equation.

CV is also known as relative standard deviation and in general, displays the size of a standard deviation to its mean.

You May Like: Paris Jackson’s Mother

To Solve Proportions Involving Direct Variation

Systematic problem solving techniques should be emphasized. It is importantto identify the independent and dependent variables. Once the relatingvariables are identified the problem may be solved as direct variation or as aproportion. Some students may want to follow a flow chart such as the onebelow:

Practice questions are readily available in math and science texts. Ask eachstudent to concoct a number of problems for the class to solve. Make sure thatthey are direct variations.

Using Variance To Assess Group Differences

Statistical tests like variance tests or the analysis of variance use sample variance to assess group differences. They use the variances of the samples to assess whether the populations they come from differ from each other.

• Sample A: Once a week
• Sample B: Once every 3 weeks
• Sample C: Once every 6 weeks

To assess group differences, you perform an ANOVA.

The main idea behind an ANOVA is to compare the variances between groups and variances within groups to see whether the results are best explained by the group differences or by individual differences.

If theres higher between-group variance relative to within-group variance, then the groups are likely to be different as a result of your treatment. If not, then the results may come from individual differences of sample members instead.

To do so, you get a ratio of the between-group variance of final scores and the within-group variance of final scores this is the F-statistic. With a large F-statistic, you find the corresponding p-value, and conclude that the groups are significantly different from each other.

Read Also: Who Are The Biological Parents Of Prince Paris And Blanket

Example : Direct Variation Through A Point

What is the constant of variation, k, of the direct variation, y = kx, through ? Through ?

Solution

The ordered pair represents an ordered pair of the format . It means that the value of x is 5 while that of y is 8. Substitute these values to the direct variation formula y = kx in order to obtain the constant of variation, k.

y = kx

8 = k

k = 8/5

The ordered pair represents an ordered pair of the format . It means that the value of x is -3 while that of y is 2. Substitute these values to the direct variation formula y = kx in order to obtain the constant of variation, k.

y = kx

Therefore, 15 workers are needed to complete a daily order of 100 baskets.