What Does The Word Sum Mean In Math Terms

The Meaning Of The Product Of A Number

The product of a number and one or more other numbers is the value obtained when the numbers are multiplied together. For example, the product of 2, 5 and 7 is

While the product obtained by multiplying specific numbers together is always the same, products are not unique. The product of 6 and 4 is always 24, but so is the product of 2 and 12, or 8 and 3. No matter which numbers you multiply to obtain a product, the multiplication operation has four properties that distinguish it from other basic arithmetic operations, Addition, subtraction and division share some of these properties, but each has a unique combination.

What Does It Mean To Simplify In Math

Simplifying in math generally refers to fractions. To simplify a fraction, find the highest number that divides into both the numerator, or the top number, and the denominator, or the bottom number. Then, divide that number into both parts of the fraction to simplify.

The highest number that divides into both parts of the fraction is called the greatest common factor. If you are trying to simplify the fraction 8/12, you find that the greatest common factor is 4. Divide the numerator by 4 to get 2. Divide the denominator by 4 to get 2. Therefore, simplifying 8/12 leads you to the answer of 2/3.

What Sum Means Kids

1 : the result obtained by adding numbers The sum of 4 and 5 is 9. 2 : a problem in arithmetic. 3 : a quantity of money We donated a small sum. 4 : the whole amount Two trips is the sum of my travel experience.

You May Like: Abiotic Meaning In Science

Look Up The Meaning Of Math Words

• Email

• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

This is a glossary of common mathematical terms used in arithmetic, geometry, algebra, and statistics.

Abacus: An early counting tool used for basic arithmetic.

Absolute Value: Always a positive number, absolute value refers to the distance of a number from 0.

Acute Angle: An angle whose measure is between 0° and 90° or with less than 90° radians.

Addend: A number involved in an addition problem numbers being added are called addends.

Algebra: The branch of mathematics that substitutes letters for numbers to solve for unknown values.

Algorithm: A procedure or set of steps used to solve a mathematical computation.

Angle: Two rays sharing the same endpoint .

Angle Bisector: The line dividing an angle into two equal angles.

Area: The two-dimensional space taken up by an object or shape, given in square units.

Array: A set of numbers or objects that follow a specific pattern.

Attribute: A characteristic or feature of an objectsuch as size, shape, color, etc.that allows it to be grouped.

Average: The average is the same as the mean. Add up a series of numbers and divide the sum by the total number of values to find the average.

Base: The bottom of a shape or three-dimensional object, what an object rests on.

Base 10: Number system that assigns place value to numbers.

Capacity: The volume of substance that a container will hold.

Sums In Ks1 And Ks2 Maths

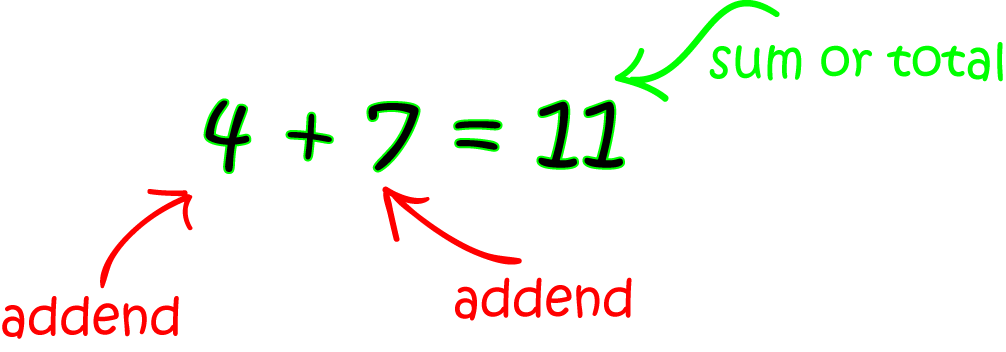
Children in Key Stage 2 need to be familiar with the word ‘sum’ as it often comes up in mental maths tests. For example:

What is the sum of 6 and 12?

What is the sum of 8, 2 and 9?

They may also carry out word problems or investigations in maths lessons which rely on them being familiar with the word, for example:

Word problem:

Investigation:

I am thinking of a two-digit number. The sum of both its digits is 9. The number is bigger than 50 and a multiple of 9. What could it be?Investigation answer: 54, 63, 72, 81 or 90

Children need to be exposed to a variety of mathematical vocabulary as often as possible, rather than just seeing numbers and symbols.

Don’t Miss: Algebra Nation Section 4 Test Yourself Answers

What Is The Sum Of All Sums

sum n., v. summed, summing. n. 1. the aggregate of two or more numbers, magnitudes, quantities, or particulars as determined by or as if by the mathematical process of addition: The sum of 6 and 8 is 14. 2. an amount or quantity, esp. of money: to lend small sums.Sum definition of sum by The Free Dictionarywww.thefreedictionary.com/sum

What Does The Word Product Mean In Math

A product is the result of carrying out the mathematical operation of multiplication. When you multiply numbers together, you get their product. The other basic arithmetic operations are addition, subtraction and division, and their results are called the sum, the difference and the quotient, respectively. Each operation also has special properties governing how the numbers can be arranged and combined. For multiplication, it’s important to be aware of these properties so that you can multiply numbers and combine multiplication with other operations to get the right answer.

TL DR

The product meaning in math is the result of multiplying two or more numbers together. To get the right product, the following properties are important:

• The order of the numbers doesn’t matter.
• Grouping the numbers with brackets has no effect.
• Multiplying two numbers by a multiplier and then adding them is the same as multiplying their sum by the multiplier.
• Multiplying by 1 leaves a number unchanged.

You May Like: Holt Mcdougal Geometry Worksheets

What Does The Word Some Mean In Math

4.7/5somenumber

Also to know is, what does the word sum mean in math?

A ‘sum‘ is the mathematical result of adding two or more numbers. The term ‘sum‘ means that you have

Likewise, what does ‘!’ Mean in math? It almost always means “and,” both in and outside of mathematics. * This symbol is called an asterisk. In mathematics, we sometimes use it to mean multiplication, particularly with computers. For example, 5*3 = 5 times 3 = 15. The open and close parenthesis.

Simply so, what does the word or mean in math?

In mathematics, “or”, formally symbolised as , does not mean “=”. In everyday usage, or and = may have similar meanings, as @sumelic points out. In logic or in mathematical logic, however, they have distinct meanings. There, “or” is a logical operator that has the value, True, if one or both operands are true.

What do you mean by some?

some pronoun an amount or number that is not known or stated: If you want more spaghetti, please take some. I like some of the people in my class. Some can also mean some people: Some have compared him to President Kennedy.

Sum Of First N Natural Numbers

As we know, a sum is the result of summation or the addition of a sequence of numbers. Thus, we can find the sum of the sequence of first n natural numbers.

First n natural numbers are:

1, 2, 3, 4,., n

This is an AP with first term a = 1 and last term l = n.

We know that, the sum of n terms of AP when the first and last terms are known is given by:

Therefore, the formula for sum of even numbers is n.

Read Also: Hbo Child Of Rage

The Arithmetic Property Of Commutation

Commutation means that the terms of an operation can be switched around, and the sequence of the numbers makes no difference to the answer. When you obtain a product by multiplication, the order in which you multiply the numbers does not matter. The same is true of addition. You can multiply 8 × 2 to get 16, and you will get the same answer with 2 × 8. Similarly, 8 + 2 gives 10, the same answer as 2 + 8.

Subtraction and division don’t have the property of commutation. If you change the order of the numbers, you’ll get a different answer. For example,

For subtraction,

Division and subtraction are not commutative operations.

The Associative Property For Products And Sums

The associative property means that if you are performing an arithmetic operation on more than two numbers, you can associate or put brackets around two of the numbers without affecting the answer. Products and sums have the associative property while differences and quotients do not.

For example, if an arithmetical operation is performed on the numbers 12, 4 and 2, the sum can be calculated as

A product example is

But for quotients

and for differences

Multiplication and addition have the associative property while division and subtraction do not.

You May Like: Geometry Unit 1 Test Answer Key

What Is A Sum

The sum of two numbers is the answer you get when you add them both together. So the sum of 5 and 4 is 9.

There was a time when teachers used the word ‘sum’ to name the following addition number sentence:

9 + 5 = 14

They would often then mistakenly use the same word to name these subtraction, multiplication and division number sentences:

9 – 4 = 57 x 3 = 2180 ÷ 10 = 8

To get round this confusion, we now refer to all of the above as number sentences.

What Is The Sum Of Two Numbers

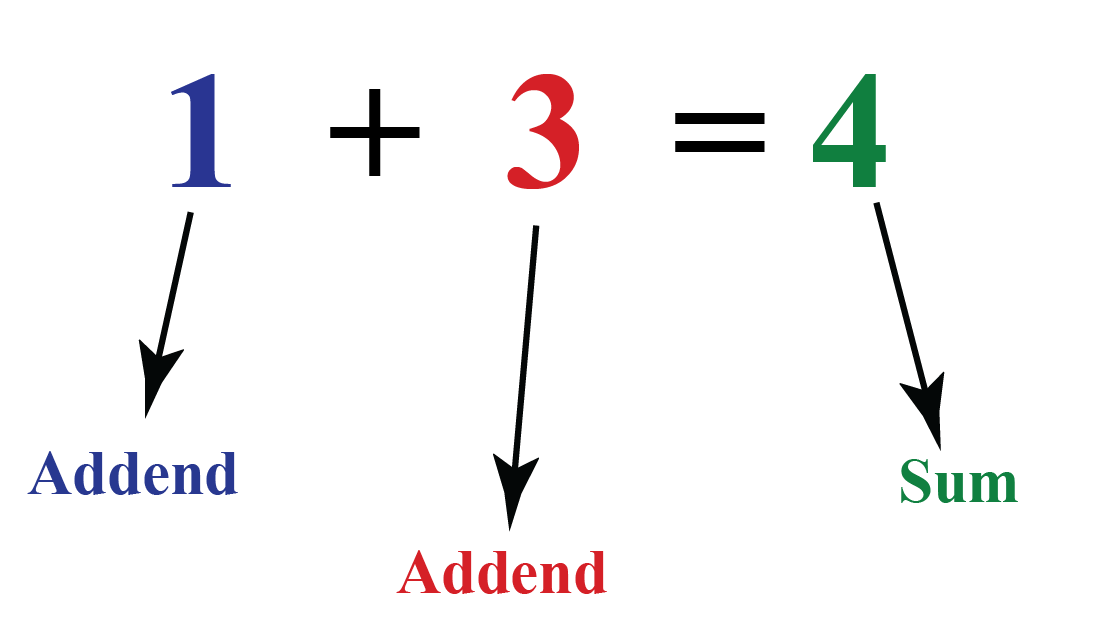
The sum of two numbers is just putting two numbers together.

Finding the sum of small numbers is not hard.

You can use your fingers to add.

Let’s look at an example to understand how to add numbers using our fingers.

Alaya is standing near a traffic signal.

She is trying to count the number of vehicles that have stopped at the red light signal.

She sees three buses at the signal.

She counts them by opening three fingers of one hand.

Next, she sees two more buses that have stopped at the signal.

She counts them by opening two more fingers.

Now, Alaya counts all the fingers opened in her hand to count the number of buses at the signal.

There are five open fingers which means that there are 5 buses at the signal.

Now, let’s see how to find a sum using a number line.

We will find the sum of 3 and 2 using a number line.

First, draw a number line and encircle the first addend 3 on it.

Now, make two jumps to the right of 3

The number you reach is 5

This is the sum.

You May Like: Algebra 2 Unit Test Edgenuity

Operational Identities Difference And Sum Vs Product And Quotient

If you perform an arithmetic operation on a number and an operational identity, the number remains unchanged. All four basic arithmetic operations have identities, but they are not the same. For subtraction and addition, the identity is zero. For multiplication and division, the identity is one.

For example, for a difference, 8 0 = 8. The number remains identical. The same is true for a sum, 8 + 0 = 8. For a product, 8 × 1 = 8 and for a quotient, 8 ÷ 1 = 8. Products and sums have the same basic properties except that they have different operational identities. As a result, multiplication and its products have a unique set of properties that you have to know to get the right answers.

Related Articles

Dividend Divisor Quotient Remainder

These Math terms relate to division. See the graphics below.

Dividend is the number to be divided.

Divisor is the number divided into or the number of groups.

Quotient is the answer you get after dividing. You can think of it as the number inside each group.

Remainder is the number left over. The remainder must always be smaller than the divisor.

If the remainder is bigger than the divisor it means the quotient is too small.

Don’t Miss: Paris Jackson Adopted

Definition Of The Summation Symbol

The symbol `\sum` indicates summation and is used as a shorthand notation for the sum of terms that follow a pattern.

For example, the sum of the first 4 squared integers, `1^2+2^2+3^2+4^2,` follows a simple pattern: each term is of the form `i^2,` and we add up values from `i=1` to `i=4.` We can write the sum compactly with summation notation as \Similarly, \We don’t have to use $i$ for the index, we could use another variable, like $j$:\begin \sum_^2 \frac & = \frac + \frac + \frac + \frac + \frac\\& = 1 + \frac + \frac + \frac + \frac\end

In general, we define the sum as:\

Cite this as

Sum Of Three Digit Numbers

Now, go through the process of finding the sum of three-digit numbers given below:

Step 1: Write the given numbers in the column by providing enough space between digits for easy understanding.

Step 2: Add the ones place digits together, transfer the carry . Finally, it gives the sum of numbers that are in the unit place.

Step 3: Add the tens place digits and carry from the previous step and transfer the carry. It gives the sum of numbers in the tens place.

Step 4: Add the digits in hundreds place digits, and carry the number from the previous step . Thus, it provides the hundreds or thousands or both of the result.

Step 5: Thus, the digits in the final row represent the sum of given numbers.

Similar procedure can be applied to find the sum of large digit numbers. Lets have a look at the example given below.

Example: Find the sum of 673 and 492.

Read Also: Kuta Software Operations With Complex Numbers