What Is Epsilon In A Function
In calculus, the – definition of a limit is an algebraically precise formulation of evaluating the limit of a function. Informally, the definition states that a limit L of a function at a point x 0 x_0 x0 exists if no matter how x 0 x_0 x0 is approached, the values returned by the function will always approach L.
How To Use Epsilon
Paul Erdös, a mathematician, may have used the best analogy to describe epsilons function he referred to epsilon as his children, and the metaphor is helpful to those of us who are not gifted in math.
When you think of children, you may be thinking of delightful little bundles of energy running around a garden or, perhaps, some demon spawn that throws things at your dog from over the fence.
Just like children, the epsilon never remains the same for long and you will likely get a headache trying to understand both children and the epsilon the larger they grow, the further away from you they get.
As mentioned previously, epsilon is a small number, almost as small as zero, but never achieving pure nothingness like zero.
For those long-suffering algebra students, epsilon is a variable similar to X or Y that theyve likely used in algebraic equations.
Epsilon is both a real number and a positive number, though it can be ridiculously small or large. Epsilon is a jack of all trades and can act as a stand-in for a wide range of numbers.
How Do I Calculate Epsilon
In mathematics, machine epsilon refers to the distance between a number and its next floating point. A machines precision is the degree to which its basic arithmetic operations are accurate. In addition to the unit roundoff, this number is also known as the unit roundoff. We have *=*1*p when the precision is p and the radix is *.
Don’t Miss: Go.hrw Algebra 1
What Does $\epsilon = \min\$ Mean
Can somebody translate the expression $\epsilon = \min\$ to plain English. Context: Mathematical Analysis, proof that an open interval is an open set.
It means that if $a-c < d-a$, then $\epsilon = a-c$, otherwise $\epsilon = d-a$. I.e., $\epsilon$ is the minimum of the set $\$, or in other words, the smaller of the two numbers.
Imagine some fixed open interval, say $ = $. Given any $a \in $, we want to come up with some radius $\epsilon$ such that the neighbourhood $$ of $a$ is completely contained inside $$. This is obtained by determining which endpoint that $a$ is closest to. For example:
- If $a = 3.1$, then we should take $\epsilon = a – c = 0.1$, since $ \subseteq $.
- If $a = 4.9$, then we should take $\epsilon = a – c = 1.9$, since $ \subseteq $.
- If $a = 5.1$, then we should take $\epsilon = d – a = 1.9$, since $ \subseteq $.
- If $a = 6.9$, then we should take $\epsilon = d – a = 0.1$, since $ \subseteq $.
More generally, we can summarize the above statements by saying:
Given any $a \in $, we should take $\epsilon = \min\$.
Does Delta Mean Change
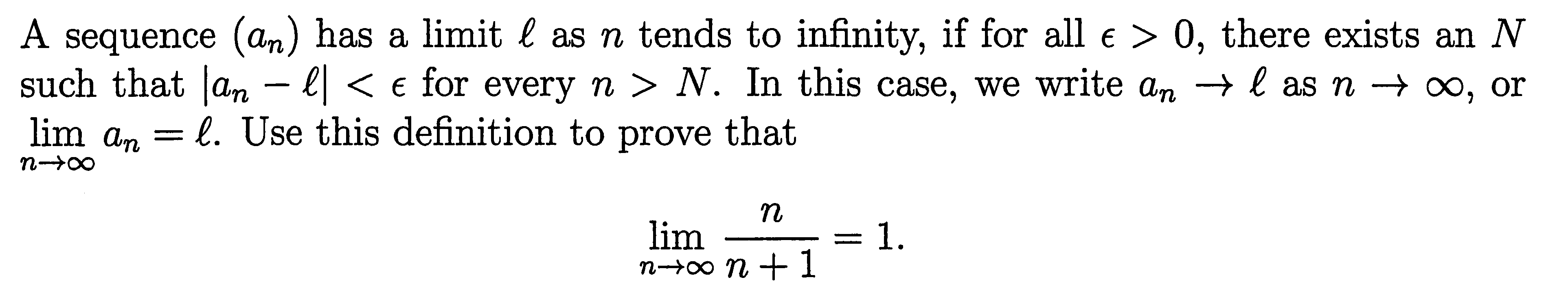
Uppercase delta at most times means change or the change in maths. Consider an example, in which a variable x stands for the movement of an object. So, x means the change in movement. Scientists make use of this mathematical meaning of delta in various branches of science.
Also Check: Geometry Book Mcdougal Littell Answers
What Is The Value Of Epsilon
As mentioned previously, epsilon can refer to any range of numbers that are not zero, but its most general usage is as a stand-in for a number between 0 and 1.
Instead of using the specific fraction or decimal to express an exact number, you can use epsilon.
The difficulty in defining epsilon comes from the fluctuating quality of the number. Since epsilon is supposed to refer to the smallest number which is closest to zero, this can be an infinite amount of numbers.
Epsilon can be 0.1 and 0.01 and 0.001, and so on. There will always be a number smaller than the fraction that you can write, and that is why epsilon is such a handy symbol.
It is a representation of a number that is too difficult or cumbersome to write.
What Does A Delta Of 05 Mean
A delta value of 0.5, therefore, tells you that for every $250 change in the value of the underlying futures, the option changes in value by about $125. At these extremes, there is a near or actual one-for-one relationship between changes in the price of the underlying asset and subsequent changes in the option price.
Don’t Miss: Algebra Nation Section 2 Test Yourself Answer Key
What Is Machine Epsilon Value
A machine-dependent floating point value, Machine Epsilon is a floating point arithmetic that is rounded in a floating point. Each floating point type has the same mathematical difference between it and the difference between it and the difference between it and the difference between it. A representation of 0 represents a value greater than 1 and a representation of 1 represents a value greater than 0.
The Epsilon Substitution Method And Arithmetic
As noted above, historically, the primary interest in the epsiloncalculus was as a means to obtaining consistency proofs.Hilberts lectures from 19171918 already note that onecan easily prove the consistency of propositional logic, by takingpropositional variables and formulae to range over truth values 0 and1, and interpreting the logical connectives as the correspondingarithmetic operations. Similarly, one can prove the consistency ofpredicate logic , by specializing tointerpretations where the universe of discourse has a single element.These considerations suggest the following more general program forproving consistency:
- Extend the epsilon calculus in such a way as to represent largerportions of mathematics.
- Show, using finitary methods, that each proof in the extendedsystem has a consistent interpretation.
For example, consider the language of arithmetic, with symbols for\, \, \, \, \. Along with quantifier-freeaxioms defining the basic symbols, one can specify that the epsilonterms \\) picks out the least value satisfying\, if there is one, with the following axiom: \ The result is a system that is strong enough to interpretfirst-order arithmetic. Alternatively, one can take theepsilon symbol to satisfy the following axiom: \
Hilberts epsilon substitution method can be described,roughly, as follows:
Recommended Reading: Unit 1 Test Geometry Basics Answer Key
Answers By Expert Tutors
The Greek lowercase epsilon , the lunate epsilon symbol , or the Latin lowercase epsilon is used in a variety of places: In mathematics , an arbitrarily small positive quantity is commonly denoted see –definition of limit.
Since you included the second symbol, we may distinguish which “epsilon” is intended.
The lunate epsilon is not to be confused with the set membership symbol . The symbol , first used in set theory and logic by Giuseppe Peano and now used in mathematics in general for set membership did, however, evolve from the letter epsilon, since the symbol was originally used as an abbreviation for the Latin word “est”. In addition, mathematicians often read the symbol as “element of”, as in “1 is an element of the natural numbers” for , for example. As late as 1960, itself was used for set membership, while its negation “does not belong to” was denoted by
What Does Appropriately Mean Answers
What Does Math Mean. Here are a number of highest rated What Does Math Mean pictures upon internet. We identified it from obedient source. Its submitted by dealing out in the best field. We give a positive response this kind of What Does Math Mean graphic could possibly be the most trending subject once we share it in google gain or facebook.
Mathematics Math Methods Learning Mathematics Math, Analysis What Does Epsilon Mean In This Formula, Solved It Is Often Stated In Math Textbooks That All, Does Acid Rain Have An Effect On Agriculture Sciencing,
Feeds.canoncitydailyrecord.com is an open platform for users to share their favorite wallpapers, By downloading this wallpaper, you agree to our Terms Of Use and Privacy Policy. This image is for personal desktop wallpaper use only, if you are the author and find this image is shared without your permission, DMCA report please Contact Us
Also Check: Prince And Paris Jackson Biological Father
What Is The Full Greek Alphabet
Here are some of the main features of the Greek alphabet: The Greek alphabet includes 24 letters: 7 vowels and 15 single and 2 double consonants. The Greek letters can be grouped into 3 categories: single and two-letter vowels /Single, double and two-letter consonants /Combinations. It is written from left to right. The letter sigma has three different forms .
Definition Of The Summation Symbol

The symbol `\sum` indicates summation and is used as a shorthand notation for the sum of terms that follow a pattern.
For example, the sum of the first 4 squared integers, `1^2+2^2+3^2+4^2,` follows a simple pattern: each term is of the form `i^2,` and we add up values from `i=1` to `i=4.` We can write the sum compactly with summation notation as \Similarly, \We don’t have to use $i$ for the index, we could use another variable, like $j$:\begin \sum_^2 \frac & = \frac + \frac + \frac + \frac + \frac\\& = 1 + \frac + \frac + \frac + \frac\end
In general, we define the sum as:\
Cite this as
Don’t Miss: Figure And Ground Psychology
Formal Definition Of Epsilon
Limit of a function
f be a function defined on an open interval around x need not be defined ) ). We say that the limit of f
\lim _ } = L, xx0limf=L,
if for every > 0 such that for all x
0 < \left| x – x_ \right |< \delta \textrm \implies \textrm \left |f – L \right| < \varepsilon. 0< xx0< fL< .
In other words, the definition states that we can make values returned by the function f f as close as we would like to the value L L by using only the points in a small enough interval around x 0 x_0 x0. One helpful interpretation of this definition is visualizing an exchange between two parties, Alice and Bob. First, Alice challenges Bob, “I want to ensure that the values of f f will be no farther than L.” If the limit exists and is indeed L L, then Bob will be able to respond by giving her a value of , “If for all points x f will always be within an L L L.” If the limit exists, then Bob will be able to respond to Alice’s challenge no matter how small she chooses
For example, in the graph for function f f below, if Alice gives Bob the value , then Bob gives her the number such that for any x x in the open interval , the value of f f lies in the interval . In this example, as Alice makes smaller and smaller, Bob can always find a smaller satisfying this property, which shows that the limit exists.
If there is any value of for which Bob cannot find a corresponding , then the limit does not exist!
For the function
A Simple Example: Linear Functions
In proper symbols, this says that \ = L\) when, for any positive number , there exists a positive number such that for any \ such that \, the function value will satisfy \-L\right|< \epsilon\).
How do we apply this definition?
In a limit proof from the definition, your objective is to find a strategy for choosing d after e is given. For most of the problems usually encountered, you can find a relation between the input closeness and the output closeness of the form |f-L|< = C|x-a| .If you can find such an inequality, then it is easy to choose d when e is given. For a function satisfying such an inequality, the output closeness is no more than C times the input closeness, so you can guarantee that the output closeness |f-L| < eif the quantity C|x-a|< e, since C|x-a| is known to be larger than |f-L|.Since C|x-a|< e if |x-a|< e/C, this suggests that we choose d as e/C. Then, if |x-a|< d = e/C, then |f-L| < = C|x-a| < C = e ,and f passes the output closeness test.
Recommended Reading: Algebra Nation Section 3 Answers Test Yourself
Thoughts On The Epsilon Delta Proof
Our video lesson will work through this style of proof in much more detail, and you will see that the proof above is only half complete, as the epsilon-delta proofs are a two-part process.
First, we use the proof to find the value of delta, and then we must redo it to prove that our choice of delta is correct. While this may seem tedious, I assure you that it will make sense with a bit of practice.
I will admit that just looking at the proof can seem scary due to all the weird letters and symbols. Still, after seeing it in action and following along with two step-by-step examples of how it is constructed in the video, you will see that this proof is quite straightforward and comes full-circle in the end. Khan Academy even calls it a beautiful proof, and after some practice I think you will see why.
Lets get to it!
What Does The Epsilon Mean In Math
epsilon is just another variable, like x, n, or T, written in Greek. In general, it is used to denote a small amount, such as an error, or perhaps a term that will be limited to a certain amount. There is a possibility that you are confusing it with the set membership symbol *, which is not the same thing.
Also Check: Molecular Shape Of Ccl4
How To Find Epsilon Delta Definition Of A Limit
Lets see if we can shine a light on what is happening.
And as Milefoot Mathematics quickly points out, we will define our limit in such a way as to allow epsilon to represent any number, while we restrict the value of delta thus, ensuring that our region is precise.
In fact, its this restriction on the delta that holds the key to this unique proof!
Lets look at a few questions to help us make sense of things.
For each of the following, sketch the open interval with point c inside. Then find the value of > 0 such that a < x < b whenever 0 < | x c | < .
Hint: delta always represents the shortest distance, so it will be your job to determine the shortest distance from either a to c or b to c!
What Does The Letter Epsilon Signify In Mathematics
- 3$\begingroup$Traditionally $\epsilon$ is used together with $\delta$ in the definition of limit, where it denotes an arbitrarily small quantity. Else, it is just a symbol that you can attach basically to anything.$\endgroup$Jul 30 ’12 at 9:52
- 2$\begingroup$First of all, I didn’t say that $\delta$ is arbitrarily small. Second, if you have several independent quantities, whatevere big or small they are, you need as many symbols, don’t you?$\endgroup$Jul 30 ’12 at 10:05
- 1$\begingroup$If you don’t say where you saw it, we can’t give you more helpful answers…$\endgroup$Jul 30 ’12 at 10:11
- 6Jul 30 ’12 at 10:38
- 6
The greek letter epsilon, written $\epsilon$ or $\varepsilon$, is just another variable, like $x$, $n$ or $T$.
Conventionally it’s used to denote a small quantity, like an error, or perhaps a term which will be taken to zero in some limit.
It’s possible that you are confusing it with the set membership symbol $\in$, which is something different. When you see $x\in X$ it means that $X$ is a set, and $x$ is a member of the set. For example,
$$1\in \$$
Hilbert’s epsilon-calculus used the letter $\varepsilon$ to denote a value satisfying a predicate. If $\phi$ is any property, then $\varepsilon x. \phi$ is a term $t$ such that $\phi$ is true, if such $t$ exists. One can define the usual existential and universal quantifiers $\exists$ and $\forall$ in terms of the $\varepsilon$ quantifier:
Here’s a not too well-known instance of the use of $\varepsilon$ in mathematics:
Recommended Reading: Algebra 1 Eoc Fsa Practice Test
Epsilon Delta Definition Of A Limit Fully Explained
Did you know that there is a formal, mathematical definition of limits?
Jenn, Founder Calcworkshop®, 15+ Years Experience
In our lessons so far, we have learned how to evaluate a limit of a function graphically and algebraically using limit laws and properties.
And while these laws and definitions enable us to evaluate limits quickly, they have a tiny flaw they arent precise.
Think about it.
Whenever we read a limit, we use the following words: approach,sufficiently close,near to, etc.
So, is there a way to be accurate in our evaluation of the limit of a function?
There sure is! And thats what this calculus lesson is all about.
Epsilon Operators In Linguistics Philosophy And Non

Reading the epsilon operator as an indefinite choice operator such that \\)) suggests that it might bea useful tool in the analysis of indefinite and definite noun phrasesin formal semantics. The epsilon notation has in fact been so used,and this application has proved useful in particular in dealing withanaphoric reference.
Consider the familiar example
The generally accepted analysis of this sentence is given by theuniversal sentence
The drawback is that a donkey suggest an existentialquantifier, and thus the analysis should, somehow, parallel in formthe analysis of sentence 3 given by 4:
but the closest possible formalization,
As pointed out by von Heusinger , this suggests that Neale iscommitted to pronouns being ambiguous between definite descriptions\-expressions) and whe-expressions. Heusinger suggestsinstead to use epsilon operators indexed by choice functions . According to this approach, the analysis of is
For every choice function \: \
Here \ is a choice function which depends on \ and theantecedent of the conditional: If \ is a choice function whichselects \\) from the set of alldonkeys, then \\) selects fromthe set of donkeys owned by \.
Recommended Reading: Is Physics Hard In College