Units For Measuring Volume
There are very big differences between units of measurement for volume. For example, there are 100 centimeters in 1 meter but there are 1,000,000 cubic centimeters in a cubic meter.
Why the big difference? Because in volume we have not just length we have length, width, and height. The sugar cube example below shows this.
How much sugar? 1 m3 or 1,000,000 cm3
Think of filling a very big box with sugar cubes .
There are 1,000,000 cm3 in 1 m3 be careful not to have too much sugar!
There are other units for measuring volume cubic inches, cubic feet, cubic yards are all units used for measuring volume. Milliliters, liters, gallons are also used especially when measuring liquids.
| Dont forget the wee 3 |
| We write cubic sizes using a small 3 next to the unit.We write mm3, cm3, m3 , km3, cm3We can say 85 centimeters cubed or 85 cubic centimeters |
How To Calculate Surface Area Of A Cube Using Volume
If you are given the volume of a cube, you can convert that into the length of one side. Then, you can use the side length to calculate the total surface area.
Use the edge length to calculate the surface area of one side, then multiply that area by 6 . This gives you the total surface area of a cube using volume.
What if you are told the total surface area of the entire cube? Can you find the volume?
Yes, the total surface area combines the area of all six, congruent faces. Find the area of one face, and then use the steps outlined above to find the volume:
How To Calculate The Volume
Here are the steps to calculate volume of any solid shape:
- Identify all the given parameters that are useful and are required to substitute in the respective volume formula. Such as the radius to be ‘r’ and height to be ‘h’, the slant height, diameter, etc.
- Make sure all the parameters are of the same units.
- Substitute the values in the volume formula of the respective shapes.
- Write the units as cubic units.
Let us understand the steps with help of an example.
Example: Find the volume of a right circular cylinder of radius 25 m and height 1 meter. Use = 3.142.
Solution:
The radius of the cylinder is, r = 25 m.Its height is h = 1 meter.Its volume of cylinder is, V = r2h = 2 = 1963.75m3.The volume of a cylinder is 1963.75 cubic meters.
Read Also: All Vault Codes For Geometry Dash
What Are The Dimensions Of A Cube
A cube is a 3D object, so a cube has three dimensions:
- Length Generally understood to be the larger of the flat dimensions.
- Width Generally understood to be the shorter of the flat dimensions.
- Height or Depth The dimension that brings the shape into our 3D world
Notice, we have two ways to describe the third dimension:
We need information about at least one of these three dimensions to measure the volume of a cube.
Volume Of Cube Using Edge Length

The measure of all the sides of a cube is the same thus, we only need to know one side in order to calculate the volume of the cube. The steps to calculate the volume of a cube using the side length are,
- Step 1: Note the measurement of the side length of the cube.
- Step 2: Apply the formula to calculate the volume using the side length: Volume of cube = 3.
- Step 3: Express the final answer along with the unit to represent the obtained volume.
Example: Calculate the volume of a cube with a side length of 2 inches.
Solution: The volume of a cube with a side length of 2 inches would have a volume of = 8 cubic inches.
Thus, it can hold a total of 8 cubes of 1 inch each. The same can be understood with the help of the given diagram.
Also Check: What Happened To Beth Child Of Rage
How Do I Use The Volume Calculator
Let’s look at the example of how to use this volume calculator:
Select the 3D shape type. If you can’t find the shape you want to calculate the volume of, choose other special dedicated calculators . In this example, let’s assume you want to calculate the volume of a cylinder.
Choose the right section of the volume calculator. In our case, it’s the part titled Cylinder volume.
Type given data into proper boxes. Our cylinder has a radius of 1 ft and a height of 3 ft. You can change the units by a simple click on the unit name.
Here you go! The volume of a chosen shape is displayed. In our case, it’s 9.42478 cu ft.
If you want to check how much that is in US barrels unit, just click on the unit name and choose barrels from the drop-down list. Our cylinder has a capacity of ~2.24 oil barrels.
Volume Of Cube Using Diagonal Formula
The volume of the cube can also be found out directly by another formula if the diagonal is known.
The diagonal of a cube is given as, 3s, where, ‘s’ is the side length of the cube. From this formula, we can write ‘s’ as, s = diagonal/3.
Thus, the volume of a cube equation using diagonal can finally be given as:Volume of the cube = /9where d is the length of the diagonal of the cube.
Note: A common mistake is to be avoided by not confusing the diagonal of a cube with the diagonal of its face. The diagonal of a cube cut through its center, as shown in the figure above. While the face diagonal is the diagonal on each face of the cube.
Don’t Miss: Algebra Connections Volume 2 Answers
Example Of Calculating Volume And Surface Area
To find surface areas of objects with a curved surface, such as a sphere, there is no choice but to memorize the volume and surface area formulas. But for other objects, we can often break them down into other recognizable polygons and shapes whose volume or surface area we can easily find. For example, with a pyramid, you simply calculate the surface area of the base and add that to the surface area of each triangular side.
Let’s find both the surface area and the volume of a square pyramid with a base length of 6 inches and a slant height of 5 inches.
How Do You Find The Height Of A Cylinder
If you have the volume and radius of the cylinder:
If you have the surface area and radius :
Don’t Miss: Paris Jackson’s Biological Parents
How Do You Find The Volume Of A Right Trapezoidal Cylinder
A right trapezoidal cylinder, also known as a rectangular prism, can be solved as such:
How To Calculate The Volume Of The Cube
To calculate the volume of a cube, we either need the measurement of its side length or the length of its diagonal.
- To find the volume using the side length of a cube, we multiply the side three times.
- In order, to calculate a cube’s volume using diagonal, we can apply the formula: /9, where d is the length of the cube’s body diagonal.
You May Like: Is Physics Easier Than Chemistry
What Is Volume Volume Definition
Volume is the amount of space that an object or substance occupies. Generally, the volume of a container is understood as its capacity not the amount of space the container itself displaces. Cubic meter is an SI unit for volume.
However, the term volume may also refer to many other things, such as
- the degree of loudness or the intensity of a sound
- the number or amount of something
- formal word for a book or one in a set of related books.
How To Calculate The Volume Of Common Shapes
Common tridimensional shapes, such as spheres, cubes, cones, cylinders, etc., have symmetry axes and features that make it possible to find analytical expressions for their volumes. This means, it is possible to write an equation to calculate the shapes volume based on its characteristics. This is done through integral calculus, so we will not go into detail about this.
Some of the analytical expressions for common shapes volumes are pretty intuitive. For example, to find the volume of a rectangular prism , we just need to calculate the area of one of the faces and then multiply it by the length perpendicular to said face, as shown in the following image.
The case of a cylinder is similar: it is a shape composed of a circular area that extends over a certain length. In this case, its volume equals the circular area times its height.
What about bodies that do not have a common shape? Take a look at the following gas tank, for example. Although at first glance it is no common shape, you could actually put some common shapes together to produce the same volume.
In this case, the volume of the entire shape can be approximated by the volume of two half spheres at both ends, and of one cylinder in the middle. This way, the total volume would be:
Don’t Miss: Similar Meaning In Math
Volume Of Cube Using Diagonal
Given the diagonal, we can follow the steps given below in order to find the volume of a given cube.
- Step 1: Note the measurement of the diagonal of the given cube.
- Step 2: Apply the formula to find the volume using diagonal: /9
- Step 3: Express the obtained result in cubic units.
Example: Calculate the volume of a cube with the diagonal measuring 3 in.
Solution:
We know, volume of cube = /9 Volume = /9 = 3 ×3 = 3 × 1.732 = 5.196 in3.
Important Notes:
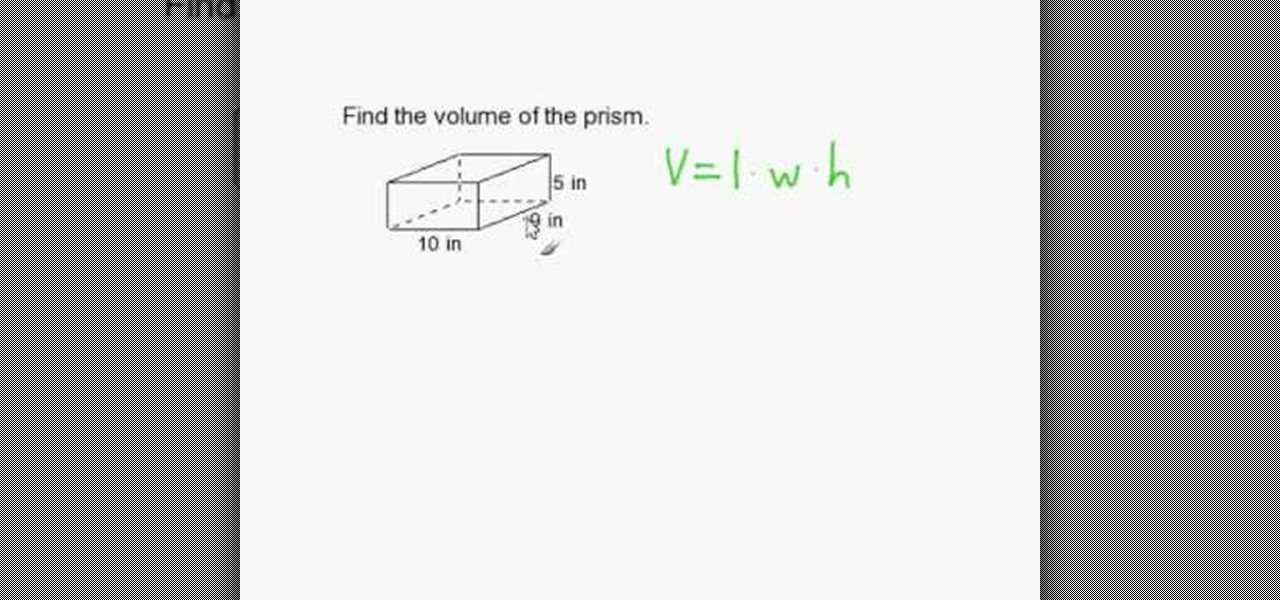
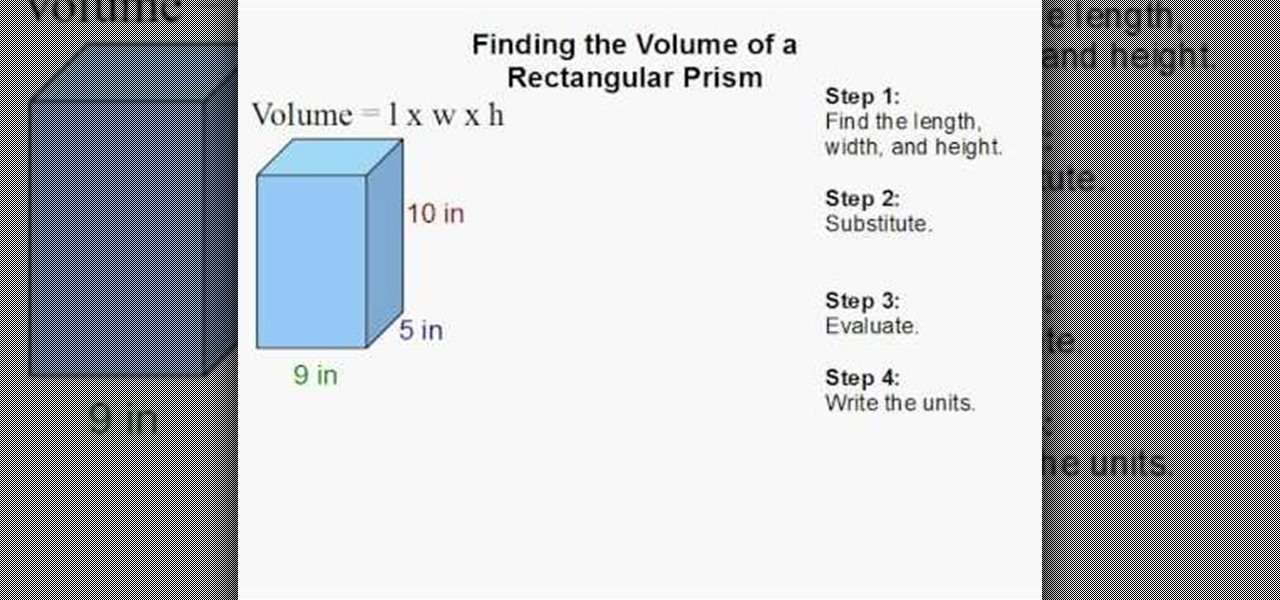
How To Find The Volume Of Prism
We can find the volume of the prism by writing the given dimensions of the prism. Then substituting the values in volume formula V = B × H where “V”, “B”, and “H” are the volume, base area, and height of the prism. Once the value of the volume of the prism is obtained, write the unit of volume of the prism in the end .
Check:
You May Like: Geometry Basics Segment Addition Postulate Worksheet Answers
Calculating The Volume Of A Regular Square Pyramid
Using A Unit Cube To Find Volume
One way to find the volume of a figure is to determine how many unit cubes it takes to fill the figure. A unit cube has side lengths of 1 and a volume of 1.
The rectangular prism below has a length of 5, width of 3, and height of 2.
You can evenly stack 2 layers of unit cubes, containing a total of 15 unit cubes each into the rectangular prism to find its volume of 30 unit cubes.
Read Also: 4.5 Practice B Geometry Answers
Finding Volume From Diagonals
What Is The Volume Of A Cylindrical Tank
volume of a cylindercylinderThe formula for calculating the volume of a cylinder with radius r and height h is:
Recommended Reading: What Does Physical Geography Mean
Worked Examples: Calculating Volume
Example 1
Calculate the volume of a cylinder with a length of 20cm, and whose circular end has a radius of 2.5cm.
First, work out the area of one of the circular ends of the cylinder.
The area of a circle is r2 . is approximately 3.14.
The area of an end is therefore:
3.14 x 2.5 x 2.5 = 19.63cm2
The volume is the area of an end multiplied by the length, and is therefore:
19.63cm2 x 20cm = 392.70cm3
Example 2
Which is bigger by volume, a sphere with radius 2cm or a pyramid with base 2.5cm square and height of 10cm?
First, work out the volume of the sphere.
The volume of a sphere is 4/3 × × radius3.
The volume of the sphere is therefore:
4 ÷ 3 x 3.14 × 2 × 2 × 2 = 33.51cm3
Then work out the volume of the pyramid.
The volume of a pyramid is 1/3 × area of base × height.
Area of base = length × breadth = 2.5cm × 2.5cm = 6.25cm2
Volume is therefore 1/3 x 6.25 × 10 = 20.83cm3
The sphere is therefore larger by volume than the pyramid.
Discovering Formulas For Volume
Students who understand volume as it is described above can reinvent for themselves many of the volume formulas that they are often asked merely to memorize. Each formula they derive helps strengthen their understanding for the other formulas they know. The volume of a solid all of whose faces are rectangles is found, as shown above, by multiplying the lengths of each of its dimensions: the product of its two base dimensions gives the area of the base, the height tells how many layers are in it, and the product of all three gives the volume.
When the faces of the figure are not all rectangles, we can sometimes dissect the figure and reassemble the pieces into a solid whose faces are all rectangles.
This material is based upon work supported by the National Science Foundation under NSF Grant No. DRL-1934161 , NSF Grant No. DRL-1741792 , and NSF Grant No. ESI-0099093 .
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
Recommended Reading: Geometry Dash All Icons Hack