Algebra 2 Adding Subtracting And Multiplying Polynomials

Multiply Monomials By Polynomials Worksheet

Multiplying polynomials practice b answers. Worksheet polynomials subtracting adding pdf key answer algebra answers math practice solutions worksheets fractions subtract. Worksheet kuta expressions rational polynomials adding dividing pdf subtracting multiplying cross fractions multiplication worksheets algebraic software division simplifying radicals algebra multiply monomials by polynomials worksheet

Multiplying Monomials with Polynomials Worksheet and Answer Key. 13 Images about Multiplying Monomials with Polynomials Worksheet and Answer Key : Multiply -divide monomials – Interactive worksheet, 27 Multiplying And Dividing Monomials Worksheet With Answers and also 27 Multiplying And Dividing Monomials Worksheet With Answers.

Adding And Subtracting Polynomials

While addition and subtraction of polynomials, we simply add or subtract the terms of the same power. The power of variables in a polynomial is always a whole number, power can not be negative, irrational, or a fraction. It is straightforward to add or subtract two polynomials. A polynomial is a mathematics expression written in the form of \.

The above expression is also called polynomial in standard form, where \ are constants, and n is a whole number. For example x2 + 2x + 3, 5×4 – 4×2 + 3x +1 and 7x – 3 are polynomials.

Adding And Subtracting Polynomials Vertically

Polynomials can be added and subtracted in vertical arrangement using the steps given below,

• Step 1: Arrange the polynomials in their standard form
• Step 2: Place the polynomials in a vertical arrangement, with the like terms placed one above the other in both the polynomials.
• Step 3: We can represent the missing power term in the standard form with “0” as the coefficient to avoid confusion while arranging terms.
• Step 4: Signs of all the polynomials remain the same in addition. While in Subtraction, the signs of the terms in subtracting polynomial change.
• Step 5: Perform the calculations

Example: + .

The given polynomials are arranged in their standard forms.

Addition performed horizontally:

• Step 1: Separate the like terms: 3×3 and x3 x2 -2x and 6x -1 and 3
• Step 2: Arrange the like terms together: 3×3 + x3 + x2 + +
• Step 3: Perform the calculations: x3 + x2 + x + = 4×3 + x2 + 4x + 2

Addition performed vertically:

• Step 1: Arrange both the polynomials one above the other with like terms place one above the other. We can represent the missing power term in the standard form with “0” as the coefficient to avoid confusion while arranging terms.
• Step 2: Perform the calculations.

Important Notes:

• The highest power of the variable in a polynomial is called the degree of the polynomial.
• The algebraic expressions having negative or irrational power of the variable are not polynomials.
• Addition and subtraction in polynomials can only be performable on like terms.

Don’t Miss: Do You Know Your Geography Worksheet Answers

Adding And Subtracting Polynomials Horizontally

Polynomials can be added and subtracted in horizontal arrangement using the steps given below,

• Step 1: Arrange the polynomials in their standard form.
• Step 2: Place the polynomial next to each other horizontally.
• Step 3: First separate the like terms.
• Step 4: Arrange the like terms together.
• Step 5: Signs of all the polynomials remain the same in addition. While in Subtraction, the signs of the terms in subtracting polynomial change.
• Step 6: Perform the calculations.

S For Adding And Subtracting Polynomials

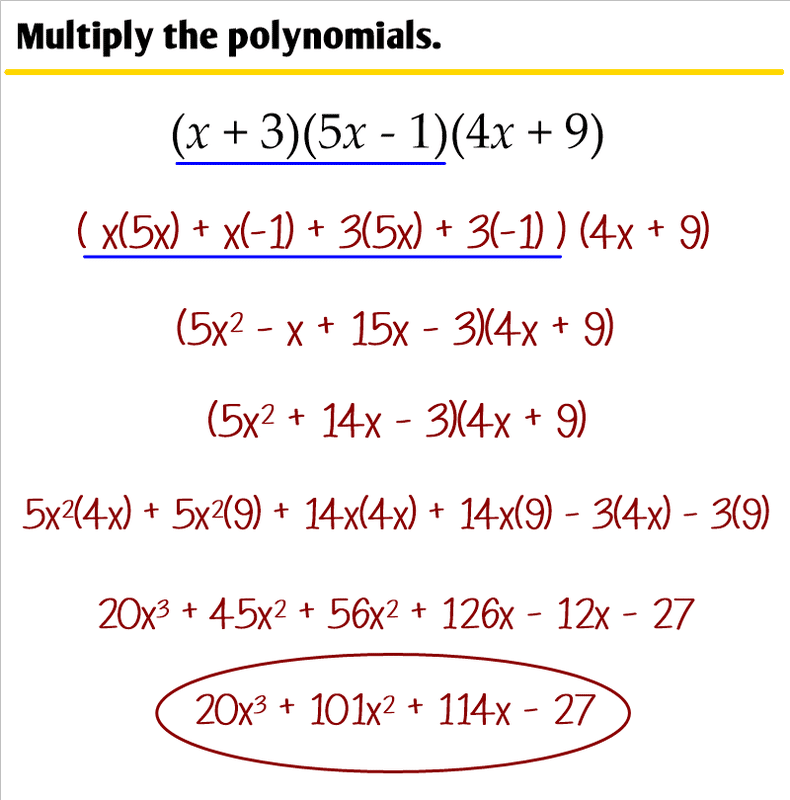
The addition or subtraction of polynomials is very simple to perform, all we need to do is to keep some steps in mind. To perform the addition and subtraction operation on the polynomials, the polynomials can be arranged vertically for complex expressions. For simpler calculations, we can perform the operation using the horizontal arrangement.

Also Check: What Is Scale In Geography

How Can We Add Polynomials

The addition of polynomials is simple. While adding polynomials, we simply add like terms. We can use columns to match the correct terms together in a complicated sum. Keep two rules in mind while performing the addition of polynomials.

• Rule 1: Always take like terms together while performing addition.
• Rule 2: Signs of all the polynomials remain the same.

For example, Add 2×2 + 3x +2 and 3×2 – 5x -1

• Step 1: Arranging the polynomial in standard form. In this case, they are already in their standard forms.
• Step 2: Like terms in the above two polynomials are:2×2 and 3×2 3x and -5x 2 and -1.
• Step 3: Calculations with signs remaining same:

Like Terms

Like Terms are terms whose variables, along with their exponents, are the same. For example, 2x, 7x, -2x, etc are all like variables.

Unlike Terms

Unlike Terms are terms whose either variables, exponents, or both variables and exponents are the not same. For example, 2, 7×2, -2y2, etc are all unlike variables.

How Do We Add Or Subtract Polynomials

Adding or subtracting polynomials is simple. While adding or subtracting polynomials we need to keep the rules for adding and subtracting a polynomial in mind. The rules can be explained as,

• Rule 1: Always take like terms together while performing addition or subtraction.
• Rule 2: Signs of all the polynomials remain the same in addition. While in Subtraction, the signs of the subtracting polynomials change.

Also Check: How To Measure Velocity In Physics

Adding Subtracting And Multiplying Polynomials Worksheet Algebra 2

Adding Subtracting And Multiplying Polynomials Worksheet Algebra 2 is a free printable for you. This printable was uploaded at July 07, 2022 by tamble in Ad.

Adding Subtracting And Multiplying Polynomials Worksheet Answers – If you’re searching for a variety of Incorporating or Subtraction worksheets you’ve identified the perfect location.

Adding Subtracting And Multiplying Polynomials Worksheet Algebra 2 can be downloaded to your computer by right clicking the image. If you love this printable, do not forget to leave a comment down below.