What Does Operation Mean In Math

How To Solve Order Of Operations

To solve the order of operations first observe the expression and note what pattern it exactly follows. Now start using either PEMDAS or BODMAS to solve the given expression. As per the rules of order of operations do look for parentheses first, then exponents, then move towards multiplication or division and addition or subtraction from left to right.

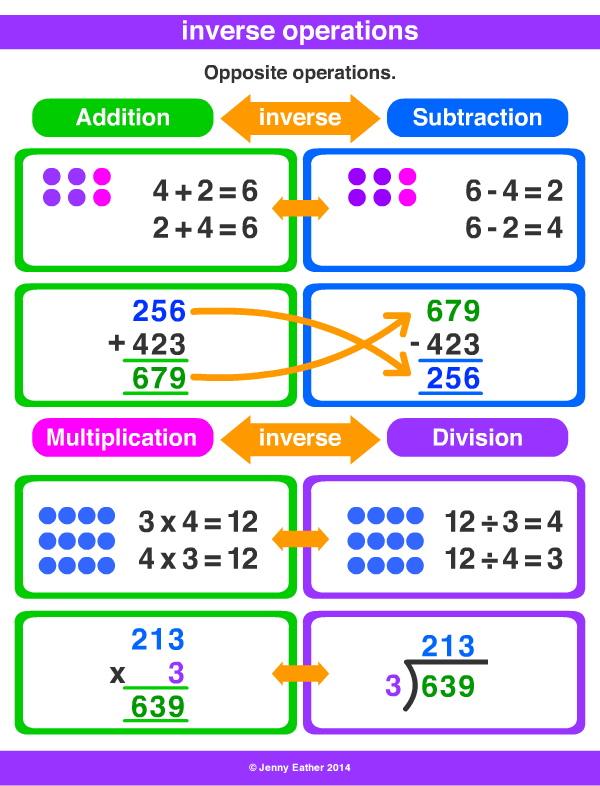
Properties Of Inverse Operations

Inverse additive property: The inverse operation of the addition of two same numbers will result in a zero.

2 + = 0

When we add a number to its opposite, the result is always 0.

Inverse multiplicative property: When we multiply a number is by its inverse, the result is always 1.

Multiplicative inverse of 10 is 110

So, 10 × 110=1

Additive Property: Consider the operation , 5 + 0 = 5

The inverse operation is, 5- 0 = 5

Thus, when we add any number to zero, both the operation and inverse operation will give the same number.

Multiplicative Property: Consider the operation, 5 × 1 = 5

The inverse operation is, 5 ÷ 1 = 5

Thus, when we multiply any number with 1, both the operation and inverse operation will give the same number.

What Are Perpendicular Lines

Perpendicular lines cross or intersect and join at right angles . Therefore, you can use perpendicular lines for many mathematical equations and patterns, serving an essential purpose.

We see perpendicular lines all around us. Any square or rectangle has perpendicular corners. You can measure the corner of any door, and you should see perpendicular lines there, too.

The origin of the word also tells us its meaning. It comes from Old French , which means forming from a right angle, which they derived from Latin , meaning plumb line .

Plumb line refers to a straight or vertical line. Perpendicular lines do require straight lines, but one does not have to be vertical, so there has been some change in meaning.

Now, we can examine how you can use perpendicular lines in math.

Recommended Reading: Prentice Hall Gold Algebra 1 Teaching Resources Answers Chapter 9

Order Of Operations Definition

As we discussed above Order of operations can be defined as, a set of basic rules of precedence we use while solving any mathematical expression, involving multiple operations. When a subexpression appears between two operators, the operator that comes first according to the list given below should be applied first. The order of operations, rules are expressed here:

• Brackets , ,

The above-mentioned set of rules always varies according to the respective given mathematical expressions.

What Does Mean In Logic

Even though and look like lowercase and uppercase versions of the same symbols, they have significantly different meanings and usage.

The smaller that we have been using means a perpendicular line. The bigger , which logicians also call the up tack symbol, is only in logic and indicates that something is always false .

You May Like: Steve Harvey Oldest Son

Rules Of Ordering In Mathematics

BODMAS is a useful acronym that tells you the order in which you solve mathematical problems. It’s important that you follow the rules of BODMAS, because without it your answers can be wrong.

The BODMAS acronym is for:

• Brackets .
• Orders .
• Division.

The Skills You Need Guide to Numeracy

This four-part guide takes you through the basics of numeracy from arithmetic to algebra, with stops in between at fractions, decimals, geometry and statistics.

Whether you want to brush up on your basics, or help your children with their learning, this is the book for you.

Or * Or Multiplication

These symbols have the same meaning commonly × is used to mean multiplication when handwritten or used on a calculator 2 × 2, for example.

The symbol * is used in spreadsheets and other computer applications to indicate a multiplication, although * does have other more complex meanings in mathematics.

Less commonly, multiplication may also be symbolised by a dot . or indeed by no symbol at all. For example, if you see a number written outside brackets with no operator , then it should be multiplied by the contents of the brackets: 2 is the same as 2×.

See our page on Multiplication for more.

Recommended Reading: Kuta Software Infinite Algebra 1 Graphing Linear Equations

Overview Of The Inverse Problem

We consider the exterior problem, as shown in Fig. 4.7. page 124. The inverse problem can be stated in measurement terms: The acoustic pressure is measured on an infinite cylindrical surface at radius r = rh, mathematically backpropagated to an inner surface at r = a, , determining the pressure and vector velocity on the inner surface. These reconstructions are done in the temporal frequency domain. In the time domain the inverse problem is equivalent to back-tracking the acoustic field in time from the outer to the inner surface, with all sources located inside or on the inner surface.

Figure 5.7. Comparison of two-hydrophone and cylindrical NAH results for the case in Fig. 5.6 but for the radial intensity. Agreement is excellent. The location of the shaker is now evident from the dense contours, at 41 cm axially and 180 degrees indicating that the driving point is the predominant region of radiation.

To reconstruct the pressure, we start with Eq. and consider r = a to be the surface which just encloses the sources in the interior, as shown in Fig. 4.7. The pressure measurement is made on the surface at r = rh. We can invert Eq. by solving for Pn ,

5.2.1Resolution of the Reconstructed Image

M.J. Nathan, in, 2010

How To Do Order Of Operations With Integers

We know that integers are positive numbers and negative numbers. We can easily perform the order of operations with integers by following the given steps:

• Look for the integers present inside the parentheses or brackets and solve them.
• After solving the integers in the parentheses, look for any integer term present in the form of exponents and solve it.
• Now we are left with the basic four operators to be performed on integers. Look for the integers with the operation of multiplication or division and solve them from the left-hand side to the right-hand side.
• Lastly, look for the integers with addition or subtraction and solve them.
• In the case of integers, we need to make sure we are properly multiplying the signs. Such that, × = + and × = –

Read Also: Who Is Paris Jackson Parents

Iib4the Operational Amplifier Or Op Amp

The op amp was so named as a result of the mathematical operations this device can perform on electronic signals. The op amp, along with a small number of resistors, can generate an output signal or voltage that is proportional to the sum of several input signals. With a slightly different configuration of resistors, the op amp can generate an output signal that is proportional to the difference of two input signals. The addition of a capacitor can create a circuit having an output signal that is proportional to the integral of the input signal.

Several op amps, resistors, and capacitors can be interconnected or configured in a manner that allows differential equations to be simulated. The excitation function or independent variable is applied to the system of amplifiers and generates an output voltage that represents the dependent variable in the differential equation. A system allowing such simulations is called an analog computer.

The op amp is also a building block in circuits that convert between an analog signal and a corresponding digital code. A circuit that accepts an analog input signal and converts this signal to a corresponding N-bit output digital code is called an analog-to-digital converter, or ADC. A circuit that accepts an N-bit digital code and converts it to a corresponding analog output signal is called a digital-to-analog converter, or DAC.

Earl G. Williams, in, 1999

A Note On Equal Precedence

Since multiplication and division are of equal precedence, it may be helpful to think of dividing by a number as multiplying by the reciprocal of that number. Thus 3 \div 4 = 3 \cdot \frac. In other words, the quotient of 3 and 4 equals the product of 3 and \frac.

Similarly, as addition and subtraction are of equal precedence, we can think of subtracting a number as the same as adding the negative of that number. Thus 34=3+. In other words, the difference of 3 and 4 equals the sum of positive three and negative four.

With this understanding, think of 13+7 as the sum of 1, negative 3, and 7, and then add these terms together. Now that youve reframed the operations, any order will work:

• +7=2+7=5
• +1=4+1=5

The important thing is to keep the negative sign with any negative number .

Don’t Miss: Core Connections Algebra Chapter 5

What Is The Meaning Behind Triangle Symbol

The triangle is a simple shape, but it has a profound meaning, which symbolizes strength in a very personal way. Deity or the divine union is the ancient symbol of the triangle. Father, Son, and Holy Ghost are all represented in this shape, which is the culmination of their minds, bodies, and spirits.

Practice Ks2 Bodmas Questions

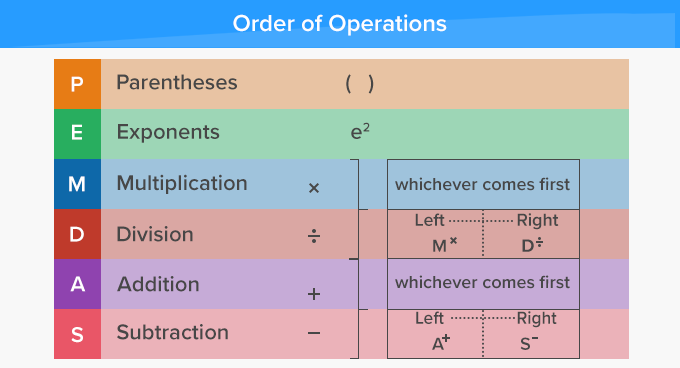
1) 29 4 x 6 + 5 =

Answer: 10

2) Write what the two missing numbers could be. x ? = 100

Answer: 6 and 10 x 10 = 100

3) Write the missing numbers to make these calculations correct.

a) 200 x ? 200 = 200

b) x 100 = 100

Answers: a) 2 b) 99

4) Write the correct sign > , < or = in each of the following

a) 9 5

b) 3 x + 5

c) / 2 10 x

Answers :

a) 9 < 5

b) 3 x > + 5

c) / 2 = 10 x

Recommended Reading: Algebra Nation Section 9 Answers Pdf

Order Of Operations Examples

< Less Than And > Greater Than

This symbol < means less than, for example 2 < 4 means that 2 is less than 4.

This symbol > means greater than, for example 4 > 2.

These symbols mean less than or equal to and greater than or equal to and are commonly used in algebra. In computer applications < = and > = are used.

These symbols are less common and mean much less than, or much greater than.

Recommended Reading: Algebra 2 Radical Worksheet

Order Of Operations Rules

While performing any sort of an operation on the respective numbers present in the expression we will follow the given basic rules in the particular sequence.

Order of Operations Rule 1: Observe the expression. The first rule is to solve the numbers present inside the parentheses or brackets. We solve inside to out grouping operations. Note the pattern of brackets present in the expression, there is a particular order to solve the parentheses, i.e., . First, solve the round brackets curly brackets box brackets . Inside the parantheses the order of operations are to be followed.Order of Operations Rule 2: After solving the numbers in the parentheses, look for any term present in the form of exponents and solve it.Order of Operations Rule 3: Now we are left with the basic four operators. Look for the numbers with the operation of multiplication or division, solve them from left to right.Order of Operations Rule 4: Lastly, look for the terms with addition or subtraction and solve them from left to right.

These rules have a specific acronym name. We call them PEMDAS or BODMAS. Let us learn now what exactly PEMDAS or BODMAS is.

How To Use Order Of Operations

Let us look at the different examples mentioned below to understand the accuracy of the rules used in order of operations.

1) For solving parentheses in order of operations:

Expression: 4 × Solution: 4 × = 28 . This is a correct way to solve the parentheses)Let us look at another approach for the same expression.4× = 20 + 2 = 22 . This is an incorrect way to solve the parentheses)

2) For solving exponents in order of operations

Expression: 4 × Solution: 4 × = 100 . This is a correct way to solve the exponents)Let us look at another approach for the same expression.4× = 202 = 400 . This is an incorrect way to solve the exponents)

3) For multiplication or division and addition or subtraction

Expression: 3 + 5 × 2Solution: 3 + 5 × 2 = 3 + 10 = 13 . This is a correct way.)Let us look at another approach for the same expression.3 + 5× 2 = 8× 2 = 16 . This is an incorrect way.)

Expression: 3 – 6 ÷ 2Solution: 3 – 6 ÷ 2 = 3 – 3 = 0 . This is a correct way.)Let us look at another approach for the same expression.3 – 6÷ 2 = ÷ 2 = -3/2 . This is an incorrect way.)

Always remember while following the rules of order of operations do multiplication or division before addition or subtraction

Recommended Reading: Paris Jackson Mom And Dad

What Does The Word Each Mean In Math

eachperaverage

. Also know, what does the word of mean in math?

Of is a powerful word in mathematics, for it can mean a fraction of something, e.g. 4/5 of 25 which commands multiplication or which can imply quotients in some cases such as probability.

Furthermore, what does total add or subtract mean math? Adding two numbers means to find their sum . Subtracting one number from another number is to find the difference between them. Multiplication means times . A product is the result of the multiplication of two numbers. Division ‘undoes’ multiplication.

Subsequently, one may also ask, what words tell you to multiply?

The Basic Operations

Conventions For Reading And Writing Mathematical Expressions

The basic principle:more powerful operations have priority over less powerful ones.

Using a number as an exponent has, in general, the most powerful effect using the same number as a multiplier has a weaker effect addition has, in general, the weakest effect . Although these terms are not used in mathematics, the sense is preserved in the language of raising 5 to the 8th power. Exponentiation is powerful and so it comes first! Addition/subtraction are weak, so they come last. Multiplication/division come in between.

When it is important to specify a different order, as it sometimes is, we use parentheses to package the numbers and a weaker operation as if they represented a single number.

For example, while 2 + 3 × 8 means the same as 2 + 24 , × 8 means 5 × 8, because the is a package deal, a quantity that must be figured out before using it. In fact × 8 is often pronounced two plus three, the quantity, times eight .

Summary of the rules:

• Parentheses first. Referring to these as packages often helps children remember their purpose and role.
• Exponents next.
• Multiplication and division next.
• Addition and subtraction last.

Recommended Reading: Is Chemistry Harder Than Physics

What Is Operation Explain

Operations is the work of managing the inner workings of your business so it runs as efficiently as possible. The specific definition of operations will depend on your industry and the stage your business is in. Sometimes, improving operations means thinking strategically about your systems and processes.

What Does A Space Mean

• $\begingroup$Look up topological space, or vector space, for two different kinds of structures.$\endgroup$Apr 23, 2012 at 21:15
• 2 The Chaz 2.0Apr 23, 2012 at 21:16
• $\begingroup$In layman’s terms, set = collection of elements. With added structure = operations on those elements + operations on subsets of those elements + properties which hold on those elements + properties which hold on subsets of those elements. So think of elements, subsets of elements, properties on those things, operations on those things.$\endgroup$ user2468Apr 23, 2012 at 22:28
• 1$\begingroup$Wikipedia defines terms that have a clear mathematical meaning, and also terms that do not. This is one of the latter. It is best to pay no attention.$\endgroup$

Think of a game like pool. It consists of the following items – a pool table, 15 different colored balls, 1 white ball and a cue stick. Let us say that you don’t know how to play pool. Now, I buy all the items mentioned above and give them to you, can you play the game of pool? You obviously can’t because you don’t know how these items are supposed to interact with each other. So, the next step would be that I explain to you how these items interact with each other and lay down some ground rules for a game of pool.

So, to learn the game of pool, I gave you two things – + .

You May Like: Algebra 2 Simplifying Radicals With Variables Worksheet Answers